Рекурсивные алгоритмы
| Загрузить архив: | |
| Файл: ref-22185.zip (162kb [zip], Скачиваний: 204) скачать |
Министерство образования Российской Федерации
Ставропольский Государственный университет
Кафедра математического анализа
Курсовая работа на тему:
«Рекурсивные алгоритмы»
Выполнил: студент3го курса ФМФ специальности ПМИ группы «Б»
Симонян Сергей Олегович
Проверил: Ионисян А. Д.
Ставрополь,
Содержание
TOC o "1-2" f h z u Введение. PAGEREF _Toc105389907 h 3
Теория рекурсивных алгоритмов. PAGEREF _Toc105389918 h 5
Дескриптивная теория. PAGEREF _Toc105389919 h 5
Метрическая теория. PAGEREF _Toc105389927 h 10
Программная реализация рекурсии. PAGEREF _Toc105389930 h 18
Общие принципы реализации. PAGEREF _Toc105389931 h 18
Пример: компилятор TurboPascal 7.0. PAGEREF _Toc105389964 h 26
Заключение. PAGEREF _Toc105389971 h 27
Список использованной литературы. PAGEREF _Toc105389977 h 28
[1].
[2].
[3], проблемы представимости матриц [4]и др.). Однако её существенным недостатком является невозможность реализации такой полезной конструкции как рекурсия.
[5].
[6]. Поэтому для дальнейшего изложения мы выберем именно теорию частично рекурсивных функций Чёрча, так как она позволяет доказать не только алгоритмическую разрешимость задач, но и существование для неё рекурсивного алгоритма.
Сначала определим и исследуем сам класс частично рекурсивных функций [7]. Данный класс определяется путем указания конкретных исходных функций и фиксированного множества операций получения новых функций из заданных.
В качестве базисных функций обычно берутся следующие:
1. Нуль- функция: 
2. Функция следования: 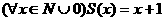
3. Функция выбора
аргументов: 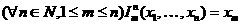
Допустимыми операциями над функциями являются операции суперпозиции (подстановки), рекурсии и минимизации.
[8], для формулировки которого введём понятие вычислимой функции.
Определение [9]. Функция называется алгоритмически вычислимой, если существует алгоритм нахождения значения функции при любом допустимом значении аргумента.
Очевидно, что функции
 ,
,
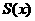 и
и 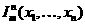 алгоритмически вычислимы.
Можно доказать, что операции суперпозиции, рекурсии и минимизации сохраняют свойство
вычислимости [10].
Значит, все частично рекурсивные функции вычислимы. Тезис Чёрча утверждает, что
класс алгоритмически вычислимых функций совпадает с классом всех частично
рекурсивных функций. То есть выполняется и обратное включение: все вычислимые функции
частично рекурсивны. Принятие данного тезиса позволяет истолковывать
доказательство, что некоторая функция не является частично рекурсивной, как
доказательство отсутствия алгоритма вычисления ее значений.
алгоритмически вычислимы.
Можно доказать, что операции суперпозиции, рекурсии и минимизации сохраняют свойство
вычислимости [10].
Значит, все частично рекурсивные функции вычислимы. Тезис Чёрча утверждает, что
класс алгоритмически вычислимых функций совпадает с классом всех частично
рекурсивных функций. То есть выполняется и обратное включение: все вычислимые функции
частично рекурсивны. Принятие данного тезиса позволяет истолковывать
доказательство, что некоторая функция не является частично рекурсивной, как
доказательство отсутствия алгоритма вычисления ее значений.
Аппарат частично
рекурсивных функций позволяет исследовать общие алгоритмические проблемы. Для
этого используется метод характеристик. Он заключается в следующем. По
конкретной задаче строится соответствующая характеристическая функция, которая затем
изучается на вычислимость. Вычислимость её позволяет утверждать разрешимость
исходной проблемы. Пусть, например, стоит проблема разрешения предиката [11].
То есть если задан 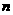
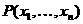
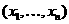 или доказать, что такого алгоритма нет. Составляем характеристическую функцию:
или доказать, что такого алгоритма нет. Составляем характеристическую функцию:

Теперь если функция 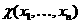 не частично
рекурсивна, то искомого алгоритма не существует. А доказательство частичной
рекурсивности сразу даёт рекурсивный алгоритм разрешения предиката.
не частично
рекурсивна, то искомого алгоритма не существует. А доказательство частичной
рекурсивности сразу даёт рекурсивный алгоритм разрешения предиката.
Аналогично теоретически можно получить рекурсивное решение любой разрешимой алгоритмической задачи. Однако практическая ценность этого метода невелика, так как доказательства часто неконструктивны, то есть показывают существование решения, но не содержат инструкций, как определить его явно. Требуется дополнительное исследование, нередко чрезвычайно трудоёмкое.
Таким образом, мы выяснили, что для любой алгоритмической задачи, допускающей решение, можно указать рекурсивный разрешающий алгоритм. То есть рекурсивные алгоритмы являются универсальным средством во всех науках использующих понятие алгоритм. С другой стороны из эквивалентности способов формализации алгоритмов по Тьюрингу и по Чёрчу следует важный вывод, что для каждого рекурсивного алгоритма можно указать итерационный, дающий тот же результат.
[12].
2.Умножение матриц. Даны две квадратные матрицы порядка 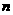 с элементами из некоторого
кольца
с элементами из некоторого
кольца 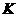 и требуется
найти их произведение. Стандартный алгоритм требует
и требуется
найти их произведение. Стандартный алгоритм требует 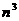 умножений и
умножений и 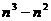 К. На первый взгляд, кажется, что
невозможно сколько-нибудь существенно уменьшить данное число операций, Однако, В.
Штрассеном [13] был
предложен следующий алгоритм.
К. На первый взгляд, кажется, что
невозможно сколько-нибудь существенно уменьшить данное число операций, Однако, В.
Штрассеном [13] был
предложен следующий алгоритм.
Пусть 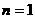
Пусть 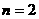 и даны матрицы
и даны матрицы 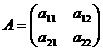
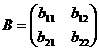
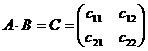
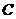 может быть вычислена
так. Пусть
может быть вычислена
так. Пусть 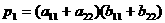
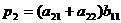
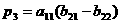
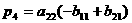
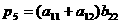
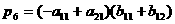

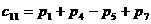
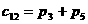
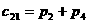 ,
, 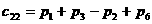 .
.
Заметим, в данном алгоритме использовано 7 умножений и 18 сложений и не использована коммутативность умножения.
Пусть теперь 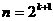
 и
и 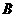 порядка
порядка  представляются как
представляются как 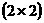
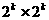 и применяется
изложенный выше алгоритм умножения
и применяется
изложенный выше алгоритм умножения 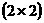
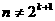
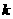 , что
, что 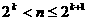 и к матрицам
добавляется нужное число нулевых строк и столбцов.
и к матрицам
добавляется нужное число нулевых строк и столбцов.
Пусть  - число арифметических
операций, используемых в алгоритме на матрицах размера
- число арифметических
операций, используемых в алгоритме на матрицах размера 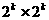
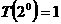 и
и 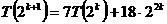
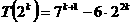
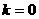 и
и 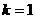 формула справедлива.
Пусть для
формула справедлива.
Пусть для 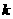 формула действительно
следует из соотношений. Имеем при
формула действительно
следует из соотношений. Имеем при 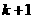
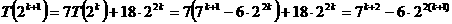 т.е. наша формула справедлива
и для
т.е. наша формула справедлива
и для 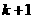
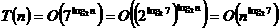
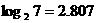
Рассмотрим теперь в общем
виде вопрос о сложности алгоритмов, использующих рекурсию. Из приведенных выше
примеров, ясно, что сложность рекурсивных алгоритмов выражается рекуррентными
соотношениями. Если в рекурсивном алгоритме используется одна процедура, то
значение сложности 
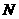
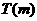 для аргументов
для аргументов  где
где 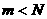
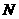 разбивается на
разбивается на 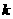 подзадач размера
подзадач размера 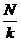
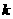 - некоторая
фиксированная константа в рекурсивном алгоритме, при этом функция сложности
- некоторая
фиксированная константа в рекурсивном алгоритме, при этом функция сложности  определяется
рекуррентным соотношением вида:
определяется
рекуррентным соотношением вида:
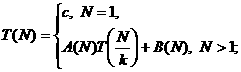
где 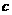 - константа,
- константа, 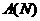
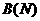 - неотрицательные, целочисленные, монотонные
функции, характеризующие сложность получения решения исходной задачи размера
- неотрицательные, целочисленные, монотонные
функции, характеризующие сложность получения решения исходной задачи размера 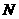 из
из 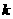 решений подзадач
размера
решений подзадач
размера 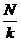
 только при значениях
аргументов
только при значениях
аргументов 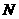 вида
вида 
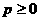 Для практических
приложений представляет интерес выделение случаев, когда решение
Для практических
приложений представляет интерес выделение случаев, когда решение  ограничено сверху
полиномом от
ограничено сверху
полиномом от 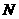
Легко доказывается, что если
функция 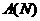 удовлетворяет условию:
существует
удовлетворяет условию:
существует 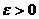
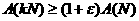 для всех натуральных
для всех натуральных 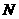
 не мажорируется сверху
никаким полиномом от
не мажорируется сверху
никаким полиномом от 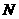 [14].
Таким образом, в дальнейшем ограничимся случаем
[14].
Таким образом, в дальнейшем ограничимся случаем 
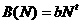 где
где
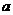
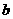
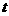 - фиксированные целые
числа.
- фиксированные целые
числа.
Теперь можно доказать, что справедливо следующее утверждение [15]. Пусть дано рекуррентное соотношение
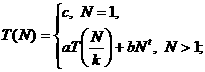
где 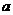
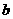
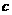
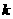
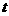 - фиксированные
константы. Тогда при
- фиксированные
константы. Тогда при 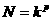
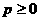
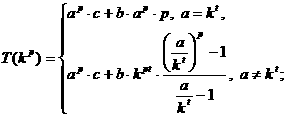
Далее вытекает следствие [16], что в предположениях предыдущего утверждения справедливы соотношения
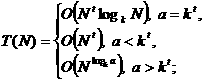
В некоторых случаях
рекурсию для задачи размера 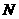 удаётся организовать
только путем аддитивного уменьшения исходного размера задачи
удаётся организовать
только путем аддитивного уменьшения исходного размера задачи 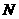 на некоторую константу
на некоторую константу
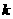
 такого типа
рекурсивных алгоритмов определяется рекуррентным соотношением вида
такого типа
рекурсивных алгоритмов определяется рекуррентным соотношением вида
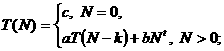
где 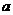
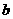
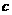
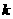
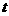 - фиксированные
константы. Например, такая ситуация возникает при решении графических задач.
Для такого соотношения при
- фиксированные
константы. Например, такая ситуация возникает при решении графических задач.
Для такого соотношения при 
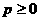 [17]
[17]

В некоторых случаях для
организации рекурсии используется «квадратичное» разбиение, при котором
исходная задача размера 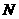 разбивается на
разбивается на 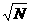 подзадач размера
подзадач размера 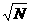
 рекурсивного алгоритма
возникает следующее рекуррентное уравнение
рекурсивного алгоритма
возникает следующее рекуррентное уравнение
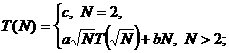
где 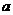
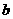
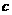 - фиксированные
константы. Оно определяет однозначно функцию
- фиксированные
константы. Оно определяет однозначно функцию  при
при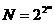 таким выражением [18]
таким выражением [18]
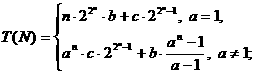
Данные результаты имеют практический интерес. В качестве примера заметим, что для задачи сортировки можно предложить рекурсивные алгоритмы, использующие как разбиение задачи на произвольное фиксированное число подзадач, так и квадратичное разбиение. Эти алгоритмы дают лучшие оценки, чем даже быстрая сортировка бинарным разбиением на подзадачи.
Для задачи умножения
матриц использование базового алгоритма умножения 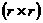
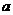 умножениями для
построения рекурсивного алгоритма, сводящего умножение
умножениями для
построения рекурсивного алгоритма, сводящего умножение 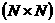
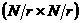

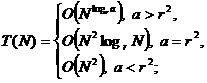
(в алгоритме Штрассена 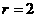
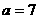
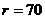 и
и 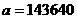 и получил
и получил 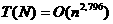
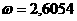
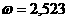
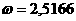
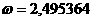
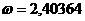
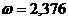
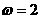 еще не решена [19].
еще не решена [19].
Рассмотрим еще один пример
применения полученных результатов. Вернемся к задаче умножения чисел в двоичной
записи. Зафиксируем натуральное число 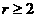 и рассмотрим два
и рассмотрим два 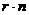
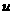 и
и 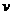
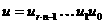
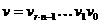
Разобьем эти числа на  частей
частей
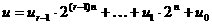
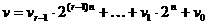 .
.
Здесь каждое  и
и 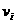
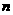
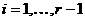
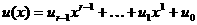
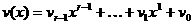
и образуем произведение 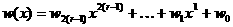

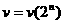
 Поэтому,
знание многочлена
Поэтому,
знание многочлена 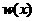 позволяет вычислить
произведение
позволяет вычислить
произведение 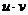 за число действий
пропорциональное
за число действий
пропорциональное 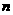
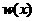 находим значение
находим значение 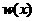 в
в 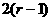 точках
точках 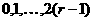
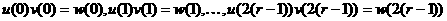
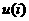 (соответственно
(соответственно 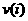 ) не превышает
) не превышает 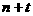 , где
, где 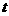 - некоторая константа,
зависящая oт
- некоторая константа,
зависящая oт  .Ясно,
что если
.Ясно,
что если  - сложность умножения
- сложность умножения 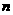
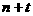
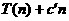 для некоторой
константы
для некоторой
константы 
Если 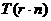 - сложность умножения
- сложность умножения 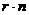
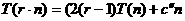 (
(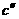 - константа). Отсюда и
согласно изложенным ранее результатам, получаем
- константа). Отсюда и
согласно изложенным ранее результатам, получаем 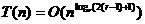
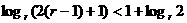 и, обозначая
и, обозначая 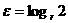 можно записать
можно записать 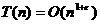
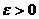 существует алгоритм
умножения
существует алгоритм
умножения 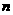
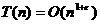
Имеются и более эффективные алгоритмы умножения чисел, но они используют уже не цифровые операции [20].
[21].
[22]. Этот подход для реализации рекурсивных программ дает возможность получать эффективные и элегантные решения для обширного класса задач.
[1] Федер Е. Фракталы. – М.: Мир, 1991.
[2] Носов В.А. Основы теории алгоритмов и анализа их сложности. –М., 1992.
[3] Клейн М. Математика. Утрата неопределённости. – М.: Мир, 1987.
[4] Носов В.А. Основы теории алгоритмов и анализа их сложности. –М., 1992.
[5] Фиошин М.
[6] Носов В.А. Основы теории алгоритмов и анализа их сложности. –М., 1992.
[7] Там же.
[8] Емельченков Е.П., Емельченков В.Е. Вычислимость. Введение в теорию алгоритмов. – М., 2000.
[9] Носов В.А. Основы теории алгоритмов и анализа их сложности. –М., 1992.
[10] Там же.
[11] Глухов М.М. Математическая логика. – М., 1982.
[12] Успенский В.А., Семёнов А.Л. Теория алгоритмов: основные открытия и приложения. – М., 1987.
[13] Носов В.А. Основы теории алгоритмов и анализа их сложности. –М., 1992.
[14] Там же.
[15] Там же.
[16] Там же.
[17] Там же.
[18] Там же.
[19] Успенский В.А., Семёнов А.Л. Теория алгоритмов: основные открытия и приложения. – М., 1987.
[20] Трахтенброт Б.А. Алгоритмы и вычислительные автоматы. – М., 1974.
[21] Кнут Д. Искусство программирования для ЭВМ, т.3. – М.: Мир, 1994.
[22] Кнут Д. Искусство программирования для ЭВМ, т.4.