Градиентные методы

	Загрузить архив:
	Файл: ref-21652.zip (24kb [zip], Скачиваний: 170) скачать

Доклад по математическому моделированию

На тему “Градиентные методы”

Студента группы ЭФП-21

Мельникова Олега

Курск 2004 год

1. Общие сведения.

Наиболее распространенные и эффективные методы приближенного решения задачи безусловной оптимизации

f(x) ® min,

(1)

где f: R^m ® R, укладываются в следующую схему. Начиная с некоторого x⁰ Î R^m, строится последовательность {xⁿ} Ì R^m такая, что

f(xn+1) < f(xn)

(2)

при всех n Î N. Такие последовательности иногда называют релаксационными, а методы построения релаксационных последовательностей — итерационными методами или методами спуска. Последовательность, удовлетворяющую (), строят в надежде, что уменьшая на каждом шаге (переходе от xⁿ к xⁿ⁺¹) значение функции, мы приближаемся к минимуму (по крайней мере, локальному).

Будем говорить, что метод, начиная с данного x⁰ Î R^m,

а) условно сходится, если последовательность {xⁿ} и

f¢(xn) ®Q при n ®¥;

б) сходится, если

xn® x* = argminf(x) при n ®¥;

в) линейно сходится (или сходится со скоростью геометрической прогрессии, или имеет первый порядок сходимости), если при некоторых C > 0 и q Î [0, 1)

||xn - x*|| £ Cqn;

(3)

г) сверхлинейно сходится, если для любого q Î (0, 1) и некоторого (зависящего от q) C выполнено неравенство ;

д) квадратично сходится (или имеет второй порядок сходимости), если при некоторых C > 0 и q Î [0, 1) и всех n Î

||xn - x*|| £ Cq2n.

, что если x не является точкой локального минимума функции f, то двигаясь из x в направлении, противоположном градиенту (еще говорят, в направлении антиградиента), мы можем локально уменьшить значение функции. Этот факт позволяет надеяться, что последовательность {xⁿ}, рекуррентно определяемая формулой

xn+1 = xn -af¢(xn),

(4)

где a - некоторое положительное число, будет .

К этой же формуле приводит и следующее рассуждение. Пусть у нас есть некоторое приближение xⁿ. Заменим в шаре B(xⁿ, e) с центром в точке xⁿ функцию f ее линейным (вернее, афинным) приближением:

f(x) »j(x) =(def) f(xn) + (f¢(xn), x - xn)

(функция j аппроксимирует f в окрестности точки xⁿ с точностью . Разумеется, (линейная) безусловная задача j(x) ® min неразрешима, если f¢(xⁿ) ¹Q. В окрестности же B(xⁿ, e) функция j имеет точку минимума. Эту точку естественно взять за следующее приближение xⁿ⁺¹.

2. Градиентный метод с постоянным шагом.

В общем случае число a в формуле может на каждом шаге (т.е. для каждого n) выбираться заново:

xn+1 = xn -anf¢(xn).

(5)

Именно методы, задаваемые формулой (), называются градентными. Если aⁿ = a при всех n, то получающийся метод называется градиентным методом с постоянным шагом (с шагом a.)

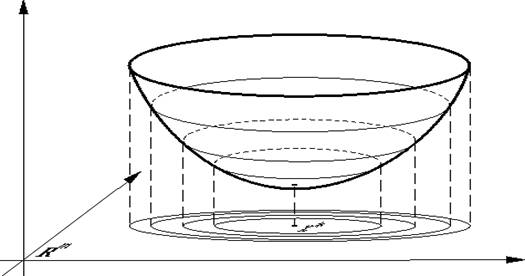
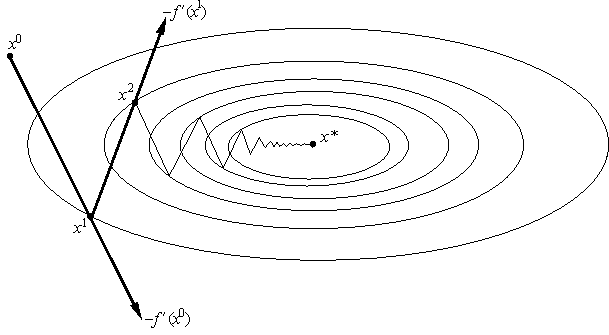
Поясним геометрическую суть градиентного метода. Для этого выберем способ изображения функции с помощью линий уровня. Линией уровня функции f (изолинией) называется любое множество вида {x Î R^m: f(x) = c}. Каждому значению c отвечает своя линия уровня (см. ).

Рис. 1.

Геометрическая интерпретация градиентного метода с постоянным шагом изображена на . На каждом шаге сдвигаемся по вектору антиградиента, "уменьшенному в a раз".

Рис. 2.

Изучим сходимость на примере функции

f(x) = |x|p,

где p > 1 (случай p £ 1 не рассматриваем, поскольку тогда функция f не будет гладкой, а мы такой случай не исследуем). Очевидно, задача с такой функцией f имеет единственное решение x* = 0. Для этой функции приближения xⁿ градиентного метода имеют вид:

xn+1 = xn -ap|xn|p-1signxn.

(6)

Пределом этой последовательности может быть только 0. Действительно, если x** = lim_n®¥ xⁿ ¹ 0, то, переходя к пределу в при n ®¥, получаем противоречащее предположению x** ¹ 0 равенство

x** = x** - ap|x**|p-1sign x**,

откуда x** = 0. Очевидно также, что если x⁰ = 0, то и xⁿ = 0 при всехn.

Покажем, что если p < 2, то при любом шаге a > 0 и любом начальном приближении x⁰ (за исключением не более чем счетного числа точек) приближения не являются сходящимися. Для этого заметим, что если 0 < |xⁿ| < (2/ap)^1/2(2-p), то

|xn+1| > |xn|.

(7)

Поэтому, если xⁿ не обращается в нуль, то она не может сходиться к нулю и, следовательно, не может сходиться вообще.

Таким образом, осталось доказать . В силу

|xn+1| = |xn -ap|xn|p-1 ·signxn| = |xn|·| 1 -ap|xn|p-2·sign xn|.

Остается заметить, что если 0 < |xⁿ| < (2/ap)^1/(2-p), то|1 -ap|xⁿ|^p-2·sign xⁿ| > 1, что и требовалось доказать.

Если p = 2, т.е. f(x) = x², то имеетвид

|xn+1| = |xn|·|1 - 2a|.

Поэтому, если aÎ (0, 1), то |1 - 2a| < 1, а следовательно,

|xn+1| = |1 - 2a|n+1·|x0| ® 0 при n ®¥.

Если же a³ 1, то

|xn+1| ³ |xn|,

и последовательность {xⁿ}, начинающаяся из ненулевой начальной точки, расходится.

Таким образом, есть функции, для которых градиентный метод не сходится даже при сколь угодно малом шаге a и есть функции, для которых он сходится только при достаточно малых шагах. В следующих пунктах рассмотрим ряд теорем о сходимости градиентного метода.

3. Теорема об условной сходимости градиентного метода с постоянным шагом.

Пусть в задаче функция f ограничена снизу, непрерывно дифференцируема и, более того, f¢ удовлетворяет :

||f¢(x) - f¢(y)|| £L ||x - y|| при всех x, y Î Rm.

Тогда приaÎ (0, 2/L) .

Д о к а з а т е л ь с т в о. Положим zⁿ = -af¢(xⁿ) и обозначим f(xⁿ + tzⁿ) через j(t).

Тогда

j¢(t) = (f¢(xn + tzn), zn)

и поэтому по формуле Ньютона— Лейбница для функции j

f(xn+1) - f(xn) = f(xn + zn) - f(xn) = j(1) -j(0) =

= ò 1 0 j¢(s) ds = ò 1 0 (f¢(xn+ szn), zn) ds.

Добавив и отняв (f¢(xn), zn) = ò01(f¢(xn), zn)ds и воспользовавшись неравенством (x, y) £ ||x||·||y||, получим

f(xn+1) - f(xn) = (f¢(xn), zn) + ò 1 0 (f¢(xn + szn) - f¢(xn), zn) ds £

£ (f¢(xn), -af¢(xn)) + ò 1 0 ||f¢(xn + szn) - f¢(xn)||·||zn|| ds.

Учитывая условие Липшица для f¢, эту цепочку можно продолжить:

f(xn+1) - f(xn) £-a||f¢(xn)||2 + L ||zn||2 ò 1 0 s ds = = -a||f¢(xn)||2 + La2 2 ||f¢(xn)||2= -a||f¢(xn)||2 æ è 1 - La 2 ö ø .

(8)

Поскольку 1 -La/2 > 0, последовательность {f(xⁿ)} не возрастает и, следовательно, {xⁿ} доказана. А так как в силу условий теоремы f еще и ограничена снизу, последовательность {f(xⁿ)} сходится. Поэтому, в частности, f(xⁿ⁺¹) - f(xⁿ) ® 0 при n ®¥. Отсюда и из получаем

||f¢(xn)||2 £a-1 æ è 1 – La 2 ö ø –1 [f(xn) - f(xn+1)] ® 0 при n ®¥.

Подчеркнем, что теорема не гарантирует метода, но лишь его , причем, .