Матроид
| Загрузить архив: | |
| Файл: ref-28868.zip (48kb [zip], Скачиваний: 68) скачать |
Введение
В алгоритмике играют важную роль жадные алгоритмы. Они просты для понимания и реализации, работают сравнительно быстро, известно много разнообразных задач, которые можно решить с помощью жадных алгоритмов. Однако не всегда можно доказать возможность применимости жадного алгоритма для нахождения точного решения многих задач. В данной статье будет рассмотрена теоретическая основа жадных алгоритмов — теория матроидов. При помощи нее можно довольно часто установить возможность применимости жадного алгоритма. Как потом выяснится, для этого необходимо, чтобы исследуемое множество являлось матроидом. Сначала будет дано определение матроида, а затем будут рассмотрены несколько стандартных задач, напрямую связанных с матроидами.
Матроид - классификация подмножеств некоторого множества, представляющая собой обобщение идеи независимости элементов, аналогично независимости элементов линейного пространства, на произвольное множество.
Аксиоматическое определение
Матроид — пара (X,I), где X — конечное множество, называемое носителем матроида, а I — некоторое подмножество множества всех подмножеств X, называемое семейством независимых множеств, то есть <![]()
. При этом должны выполняться следующие условия:>
<

>Если <
и
, то
>Если <
и мощность А больше мощности В, то существует
такой, что
>
Базами матроида называются максимальные по включению независимые множества.
Определение в терминах правильного замыкания
Пусть <
- частично упорядоченное множество.
- замыкание в ![]()
, если:>
Для любого х из Р: <

>Для любых х,у из Р: <

>Для любого х из Р: <
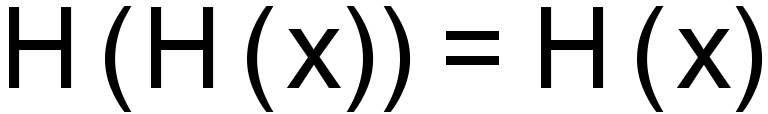
>
Рассмотрим <
случай, когда частично упорядоченное множество - булева алгебра. Пусть
- замыкание ![]()
.>
1. Замыкание правильно (аксиома правильного замыкания), если <![]()
>
2. Для любого <
существует такое ![]()
, что>
1. <![]()
>
2. <![]()
>
Пара <
, где
- правильное замыкание на ![]()
, называется матроидом.>
Примеры
Универсальный матроид <
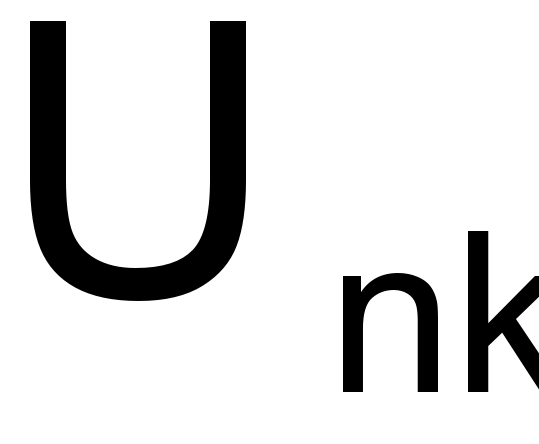
. Множество X имеет мощность n, независимыми множествами являются подмножества мощностью не больше k. Базы — подмножества мощностью k.>Графический матроид. Множество X — множество ребер графа, независимые множества — ациклические подмножества этих ребер. Базами являются остовные леса графа.
Матричный матроид. Семейство всех линейно независимых подмножеств любого конечного множества векторов произвольного непустого векторного пространства является матроидом.
Определим множество E, как множество состоящее из {1, 2, 3, .., n} — номеров столбцов некоторой матрицы, а множество I, как множество состоящее из подмножеств E, таких, что векторы, определяемые ими, являются линейно независимыми над полем вещественных чисел R. Зададимся вопросом — какими свойствами обладает построенное множество I?
1. Множество I непусто. Даже если исходное множество E было пусто — E = , то I будет состоять из одного элемента — множества, содержащего пустое. I = { {} }. |
2. Любое подмножество любого элемента множества I также будет элементом этого множества. Это свойство понятно — если некоторый набор векторов линейно независим над полем, то линейно независимым будет также любой его поднабор. |
3. Если A, B I, причем |A| = |B| + 1, тогда существует элемент x B A, такой что B {x} I. |
Докажем, что в рассмотренном примере множество линейно независимых столбцов действительно является матроидом. Для этого достаточно доказать третье свойство из определения матроида. Проведем доказательство методом от противного.
Доказательство. Пусть <
и
. Пусть W будет пространством векторов, охватываемым
. Понятно, что его размерность будет не менее
. Предположим, что
будет линейно зависимо для всех
(то есть третье свойство не будет выполняться). Тогда B образует базис в пространстве W. Из этого следует, что
.Но так как по условию A и B состоят из линейно независимых векторов и ![]()
, получаем противоречие. Такое множество векторов будет являться матроидом.>
Дополнительные понятия
Двойственным данному матроиду называется матроид, носитель которого совпадает с носителем данного матроида, а базы — дополнения баз данного матроида до носителя. То есть X*=X, а множество баз двойственного матроида — это множество таких B*, что B*=XB, где B — база данного матроида.
Циклом в матроиде называется такое множество AX, что AI, и для любого BA, если BA, то BI
Рангом матроида называется мощность его баз. Ранг тривиального матроида равен нулю.
Матроид Фано
<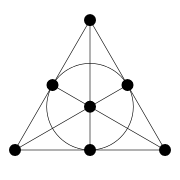
Матроиды с маленьким числом элементов часто изображают в виде диаграмм. Точки — это элементы основного множества, а кривые «протянуты» через каждую 3-ех елементную цепь (3-element circuit). Диаграмма показывает 3-ранговый матроид, называемый матроидом Фано, пример, который появился в 1935 в статье Уитни (Whitney).>
Название возникло из того факта, что матроид Фано представляет собой проективную плоскость второго порядка, известная как плоскость Фано, чьё координатное поле — это двух-элементное поле. Это означает, что матроид Фано — это векторный матроид, связанный с семью ненулевыми векторами в трехмерном векторном пространстве над полем 2ух элементов.
Из проективной геометрии известно, что матроид Фано непредставим произвольным множеством векторов в вещественном или комплексном векторном пространстве (или в любом векторном пространстве над полем, чьи характеристики отличаются от 2).
Графовый матроид
Граф неориентированный и состоит из четырех вершин и семи ребер, одно из которых является петлей. Пусть E будет множеством, состоящих из ребер этого графа,<
, а I будет множеством подмножеств E, таких что каждый элемент I не содержит в себе циклов графа. Эта пара множеств E, I является матроидом, ее называют графовым матроидом и обозначают M(G).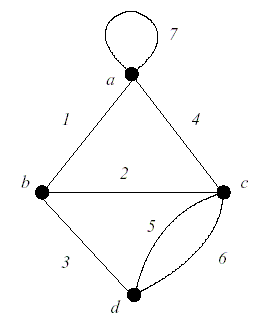
>
Теорема
Пусть G — граф, а <
— его матрица инциденций. Если рассматривать
как матрицу над полем {0,1}, где все операции выполняются по модулю 2, то тогда векторный матроид, построенный на
, в качестве независимых множеств будет содержать множества ребер, не содержащих в себе циклов, и ![]()
.>
Доказательство. Необходимо доказать, что <![]()
линейно зависим тогда и только тогда, когда X содержит цикл. Предположим, что X содержит в себе цикл C. Если C — это петля, то тогда в X будет содержаться нулевой вектор и он будет линейно зависимым. Если же C не петля, то каждая вершина в этом цикле будет соответствовать двум ребрам C и сумма векторов по модулю 2 будет нулевым вектором. Из-за чего X будет линейно зависимым. >
Теперь предположим, что X линейно зависимый. Возьмем минимальное линейно зависимое подмножество D из X (то есть такое подмножество, что удаление из него любого элемента приводит к тому, что оно будет линейно независимым). Если D будет состоять из нулевого вектора, то тогда X содержит петлю и, соответственно, цикл.
Если D не содержит нулевого вектора: так как в поле {0,1} существует единственный ненулевой элемент — 1, то сумма векторов из D будет нулевым вектором, из-за того, что D — минимальное линейно зависимое подмножество. Из этого следует, что D содержит ребра из цикла, и если какой-то вершине инцидентно ребро из D, то существует как минимум еще одно ребро, инцидентное ей. Действительно, возьмем ребро <
и пусть вершины
и
соответствуют этому ребру. Пусть вершине
инцидентно еще какое-то ребро
. Пусть вершина
будет другим концом ребра
. Продолжим этот процесс. В результате будут получены две последовательности —
и ![]()
. Так как количество вершин в D конечно, то какая-то из вершин v должна повториться. Когда это произойдет, то в D будет найден цикл. Соответственно цикл будет найден и в X.>
Матроиды и комбинаторная оптимизация
Матроиды имеют широкое применение в задачах, связанных с комбинаторной оптимизацией, а также с задачами, решение которых основано на жадных алгоритмах.
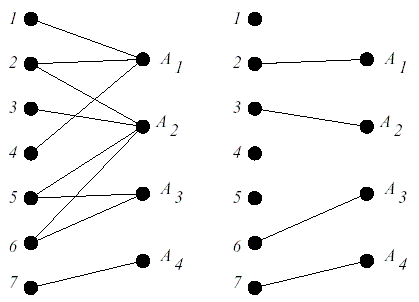
Рассмотрим такую задачу: у менеджера есть m однодневных работ для одного человека <![]()
. Также он располагает n рабочими, каждый из которых умеет выполнять какой-то поднабор работ. Менеджер хочет знать, какое максимальное количество работ способны выполнить его рабочие за один день. Как позже выяснится, это будет рангом некоего матроида.>
<
>
Пусть A — множество подмножеств некоего множества E. К примеру, пусть A=({1,2,4},{2,3,5,6},{5,6},{7}), при множестве E={1,2,3,4,5,6,7}. Подмножество E — <
называется частичным трансверсалем A, если есть взаимооднозначное соответствие Ф между {1,2,…,k} и {1,2,…,m}, причем ![]()
для любых i. Если m = k, то такой частичный трансверсаль называется трансверсалем. Если взять множество {2,3,6,7}, то оно будет трансверсалем для A, как это видно из рисунка слева.>
Теоремы
Все базы матроида имеют одинаковую мощность.
Матроид однозначно задается носителем и базами.
Цикл не может быть подмножеством другого цикла.
Если <
и
— циклы, то для любого

содержит цикл>Если B — база и xB, то B{x} содержит ровно один цикл.
Литература
1. Асанов М.О. и др. Дискретная математика: графы, матроиды, алгоритмы. — Ижевск: ННЦ "Регулярная и хаотическая динамика", 2001. — С. 288.
2. Ковалев М.М. Матроиды в дискретной оптимизации. Изд.2, 2003. 224 с. 142 руб.
Содержание
Введение…………………………………………………………………………………………………………1
Аксиоматическое определение………………………………………………………1
Определения в терминах правильного замыкания…………1
Примеры……………………………………………………………………………………………………………2
Дополнительные понятия……………………………………………………………………3
Матроид Фано………………………………………………………………………………………………3
Графовый матроид……………………………………………………………………………………4
Матроиды и комбинаторная оптимизация………………………………5
Теоремы……………………………………………………………………………………………………………6
Литература……………………………………………………………………………………………………7
Министерство образования и науки Украины
Запорожский национальный университет
Кафедра дискретной математики
Реферат
По дискретной математике
На тему:
«Матроид»
Работу выполнила
Студентка гр. 4328-1
Спец. Информатика
Рудоман Евгения Валериевна
Работу проверила
Бакурова Анна Владимировна
Запорожье, 2009