Сравнения высших степеней(Конгруенції вищих степенів )

Разделы	Математика
Тип	Рефераты
Формат	Microsoft Word
Язык	Украинский
	Загрузить архив:
	Файл: ref-10203.zip (50kb [zip], Скачиваний: 84) скачать

[1]:

f(х)= а₀х^п + а₁х^п-1 + . . . + а_n-1x + a_n ≡ 0 (mod p), n≥1,           (1)

де a₀≠0 (mod p) і р — просте число.

Теорема 1. Конгруенцію (1) завжди можна так перетворити що її старший коефіцієнт дорівнюватиме одиниці.

Справді, через те що р — просте і a₀ не ділиться на р, то завжди існує єдине число α, що а₀α ≡ 1 (modp). Помноживши тепер конгруенцію (1) на α і замінивши а₀x одиницею, дістанемо еквівалентну   конгруенцію з старшим коефіцієнтом, що дорівнює одиниці:

xⁿ + b₁x^n-1+ .. + b_n-1x + b_n ≡ 0 (mod p);                     (1')

тут b_i ≡ a_iα (mod p).

Теорема 2. Якщо степінь конгруенції (1) не менший від модуля конгруенції, то вона еквівалентна деякій конгруенції степеня, не вище за р—1 (за тим самим модулем).

Справді, поділимо f(х) на х^р-х; і частку від ділення позначимо через q(x), а остачу через r(х). Тоді на підставі алгоритму ділення з остачею дістанемо:

f(x) = (x^p—x)q(x) + r(x),

де частка q(х) і остача r(х) будуть многочленами з цілими коефіцієнтами, причому степінь r(х) буде не вище р—1. За теоремою Ферма x^p—-x ≡ 0 (mod p) при будь-якому цілому х, тому дістанемо тотожну конгруенцію:

f(х) ≡ r(x) (mod р).

Ця тотожна конгруенція показує, що корені конгруенції (1) і конгруенції   r(х)≡0 (mod р) однакові. Оскільки х^р — х завжди ділиться на p, то f(x) і r(x)можуть ділитись на p тільки одночасно; отже, конгруенції

f(х) ≡ 0 (mod р) і r(х) ≡ 0 (mod р)

еквівалентні. Через те що степінь r(x) менше за p, то теорему доведено.

Зокрема, може статись, що f(x) ділиться на x^p—-x , тобто r(х) ≡ 0 (mod р) – тотожна конгруенція за модулем p, тобто остача при діленні конгруентна з нулем і дана конгруенція еквівалентна конгруенції 0 ≡ 0 (mod p) та справедлива при будь-якому цілому x. Далі, нехай остача від ділення f(х) на x^p—-x є многочлен нульового степеня, що дорівнює b_p-1. Якщо b_p-1 не ділиться на p, то дана конгруенція не має розв’язків, бо вона зводиться до невірної конгруенції :

b_p-1≡ 0 (mod p).

Приклад. Якій конгруенції нижче від 5-го степеня еквівалентна конгруенція:

f(х) = х¹⁷ + 2x¹¹ + Зx⁸ — 4x⁷ + 2x — 3 ≡ 0 (mod 5).

Поділивши f (х) на х⁵ — х і замінивши всі коефіцієнти остачі найменшими невід'ємними лишками за модулем 5, дістанемо, що дана конгруенція еквівалентна конгруенції

r(х) = Зx⁴ + Зx³ + Зx + 2 ≡ 0 (mod 5).

Зауваження. Можна вказане ділення на х^p — х фактично і не виконувати, а просто замінити хⁿ на х^r, де r > 0 є остача від ділення п на р — 1. Справді, за теоремою Ферма х^р ≡ х (mod р), звідси x^p+1 ≡ x², x^p+2 ≡ x³, ... і взагалі:

Через те що в нашому прикладі x¹⁷ можна замінити через х, а 2x¹¹ через 2x³,Зx⁸   через Зx⁴,—4x⁷ замінити через —4x³ ≡ x³ , тому відразу дістанемо:

f(x) ≡ Зx⁴ + Зx³ + Зx + 2 ≡ 0 (mod 5).

У свою чергу, останню конгруенцію можнаспростити так: х ≠ 0 (mod 5), тому x^5-1 ≡ 1 (mod 5) і

f(x) ≡ Зх³ + Зх ≡ 0 (mod 5),

або

f(x) ≡ х² + 1 ≡ 0 (mod 5).

Очевидні розв'язки останньої конгруенції x ≡ 2, 3 (mod 5) будуть також і розв'язками даної конгруенції:

f(x) ≡ 0 (mod 5).

Теорема 3. Якщо α₁—який-небудь   розв'язок   конгруенції   (1), то має місце тотожна конгруенція:

f (х) ≡ (х — α₁)f₁(х) (mod р),                              (2)

де f₁(х) — многочлен степеня, на одиницю нижчий від степеня многочлена f(x). Старший коефіцієнт многочлена f₁(x)збігається з старшим коефіцієнтом даного многочлена fix).

Справді, поділимо f(x) на х — α₁   і   частку   позначимо   через f₁(х), а остачу через r. За теоремою Безу r = f(α₁), але

f(α₁) ≡ 0 (mod p)

за умовою, тоді конгруенцію

f(x) = (x – α₁) f₁(x) + f(α₁) ≡ 0 (mod р)

можна переписати так:

f(x) ≡ (x-α₁)f₁(x) (mod p).

При цьому кажуть, що f(х) ділиться на х — α₁ за модулем р. Очевидно, що й навпаки: з конгруенції (2) випливає, що f(α₁) ≡ 0 (mod p) тобто α₁ — корінь конгруенції (1); отже, маємо такий висновок.

Висновок. Конгруенція (1) має корінь х = α₁тоді і тільки тоді, коли ліва її частина f(x) ділиться на х — α₁ за даним модулем р.

Зауважимо, що теорема 3 і висновок з неї справедливі і для складеного модуля т.

Теорема 4. Якщо α₁, α₂, . . , α_k (k ≤n)є різні розв'язки конгруенції (1), то має місце тотожна конгруенція:

f (х) ≡ (х – α₁) (х - α₂) . . . (х - α_k) f_k (x)(mod p),                (3)

де степінь f (х) дорівнює п — k і старші коефіцієнти у f(x) і f_k(x) однакові.

Справді, згідно, з теоремою 3 конгруенція (1) еквівалентна конгруенції

(x - α₁)f₁(x) ≡ 0 (mod p).(2¹)

Через те що α₂ є розв'язок конгруенції (1), то, підставляючи його в еквівалентну конгруенцію (2'), дістанемо тотожну конгруенцію:

(α₂ — α₁)f₁(α₂) ≡ 0 (mod р).

Але добуток двох чи кількох чисел ділиться на просте число р тоді і тільки тоді, коли на р ділиться принаймні один з співмножників. За умовою α₁ і α₂ різні, тобто

α₁≠α₂ (mod p),

отже, α₂ — α₁ не ділиться на р, а тому f₁(α₂) ділиться на р, тобто    f₁(α₂) ≡ 0 (mod p); останнє означає, що α₂ — розв'язок конгруенції f₁(x)≡0 (mod p). За теоремою 3 дістанемо:

f₁(х)≡(x-α₂)f ₂(x) (mod p);

звідки

f(x)≡(x-α₁)(x-α₂)f₂(x) (mod p).

Аналогічно міркуючи, кінець кінцем прийдемо до тотожної конгруенції (3). З самого процесу одержання многочленів f₁(x), f₂(x),… f_k (x) видно, що старші коефіцієнти цих многочленів однакові і дорівнюють старшому коефіцієнтові a₀ многочлена f(x).

В и с н о в о к. Якщо конгруенція (1) п-го степеня за простим модулем р (п можна вважати не більшим за р — 1) має п різних розв'язків α₁, α₂, . . , α_n, то має місце тотожна конгруенція:

f(x) ≡ а₀ (х — α₁) (х — α₂) ... (х — α_n) (mod p).                      (4)

Справді, тут k= п, отже, степінь многочлена f_n(x)дорівнюватиме п-n=0, тобто f_n (х) = а₀.

[2]

Це випливає з того, що числа 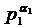, , 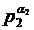..., 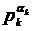попарно взаємно прості.

Отже, все зводиться до того, що доводиться окремо досліджувати і розв'язувати конгруенції виду

f(x) ≡ 0 (mod 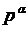),                                           (4)

де p— просте  число, α — ціле додатне число. Зауважимо, що всякий розв'язок конгруенції (4) буде розв'язком конгруенції

f(x) ≡ 0 (mod p).                                           (5)

Очевидно, якщо конгруенція (5) не має розв'язків, то й конгруенція (4) розв'язків не матиме. Справді, з припущення виходить, що при жодному цілому х не має місця конгруенція

f(x) ≡ 0 (mod p),

тобто f(х) не ділиться на р, алетоді f(х) і поготів   не ділитиметься на p^α, тобто

f(x) ≠ 0 (mod )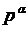

ні при якому цілому х.

[1]Рівняння

a₀xⁿ+a₁x^n-1+…+a_n-1x+a_n=pt                                                                             (*)

з цілими коефіцієнтами і p>1 еквівалентне конгруенції (1). Внаслідок такої залежності задачу на розв’язання рівняння (*) в цілих числах можна замінити задачею про розв’язання конгруенції (1), що і застосовується в теорії чисел.

[2]З цієї причини в теорії конгруенцій звичайно приймають, що модуль конгруенції – просте число або степінь простого числа.