Сингулярное разложение в линейной задаче метода наименьших квадратов
| Сдавался/использовался | Математический факультет/ Кафедра прикладной математики/Владикавказ/2002 |
| Загрузить архив: | |
| Файл: diiplom.zip (244kb [zip], Скачиваний: 93) скачать |
[1] и унитарна[2]. Предположим, что дан
вектор х размерности m, тогда существует матрица H
такая, что 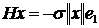
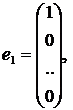
а s = +1, при положительной первой компоненте вектора х и = –1, при отрицательной.
Доказательство.
Положим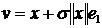 действительная
матрица. Любую действительную матрицу можно привести в треугольному виду
действительная
матрица. Любую действительную матрицу можно привести в треугольному виду
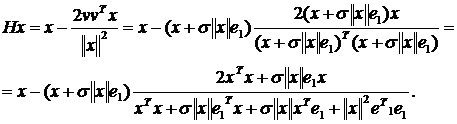
Далее принимаем во внимание то, что 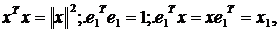 и получаем следующее:
и получаем следующее:
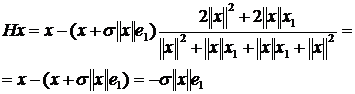
[3] матрицы А; это положительные значения квадратных
корней 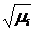 из собственных
значений
из собственных
значений 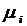 матрицы АТА (которая при
невырожденной матрице А положительно
определена[4], в противном случае
положительно полуопределена (неотрицательно определена[5]) и поэтому имеет только
вещественные собственные значения ³ 0). Для вещественных симметричных матриц
сингулярные числа равны абсолютным величинам собственных значений:
матрицы АТА (которая при
невырожденной матрице А положительно
определена[4], в противном случае
положительно полуопределена (неотрицательно определена[5]) и поэтому имеет только
вещественные собственные значения ³ 0). Для вещественных симметричных матриц
сингулярные числа равны абсолютным величинам собственных значений: 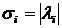
Умножение вектора х на матрицу А приводит к новому вектору Ах, норма которого может очень сильно отличаться от нормы вектора х.
Область изменений может быть задана двумя числами
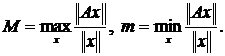
Максимум и минимум берутся по всем ненулевым векторам. Заметим, что если А вырождена, то m=0. Отношение M/m называется числом обусловленности матрицы А,
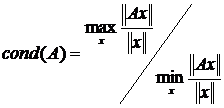 (7)
(7)
Рассмотрим норму обратной[6] матрицы 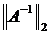
Для матрицы А
существует сингулярное разложение 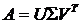
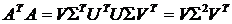
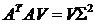
 и
и 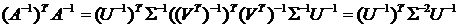
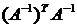 – 1/
– 1/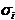 есть величины, обратные
собственным числам матрицы
есть величины, обратные
собственным числам матрицы 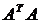 –
– 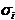
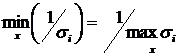
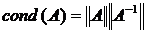
Рассмотрим систему уравнений Ax=b, и другую систему, полученную изменением правой части: A(x+Dx)=b+Db . Будем считать Db
ошибкой в b, а Dx соответствующей ошибкой в x, хотя нам нет необходимости считать ошибки малыми. Поскольку A(Dx)=Db, то определения M иm немедленно приводят к неравенствам 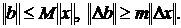 Следовательно , при m¹0,
Следовательно , при m¹0,
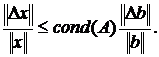
Величина 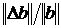 есть относительное
изменение правой части, а величина
есть относительное
изменение правой части, а величина 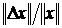 – относительная
ошибка, вызванная этим изменением. Аналогичные выкладки можно провести не
только с элементами вектора правой части но и с элементами самой матрицы А и
найти зависимость между относительным изменением элементов матрицы и
относительной ошибкой вызванной этим изменением. Отсюда следует, что число
обусловленности выполняет роль множителя в увеличении относительной ошибки.
– относительная
ошибка, вызванная этим изменением. Аналогичные выкладки можно провести не
только с элементами вектора правой части но и с элементами самой матрицы А и
найти зависимость между относительным изменением элементов матрицы и
относительной ошибкой вызванной этим изменением. Отсюда следует, что число
обусловленности выполняет роль множителя в увеличении относительной ошибки.
Приведем некоторые свойства числа обусловленности. Ясно, что
M³m
и поэтому cond(А)³1.
Если Р – матрица перестановок[7], то компоненты вектора Px лишь порядком отличаются от компонент
вектора х. Отсюда следует, что 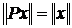 и cond(P)=1 . В частности cond(I)=1.
Если А умножается на скаляр с, то cond(cА)= cond(А). Если D
– диагональная матрица, то
и cond(P)=1 . В частности cond(I)=1.
Если А умножается на скаляр с, то cond(cА)= cond(А). Если D
– диагональная матрица, то 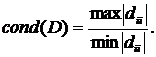
[8] а также используется алгоритм со сдвигом. Форма Хессенберга представляет из себя верхнюю треугольную матрицу (верхняя форма Хессенберга) у которой сохранена одна диагональ ниже главной, а элементы ниже этой диагонали равны нулю. Если матрица симметрична, то легко видеть, что матрица Хессенберга превращается в трехдиагональную матрицу[9]. При использовании матрицы Хессенберга время процесса пропорционально n2, а при использовании трехдиагональной матрицы – n.
Можно использовать другие соотношения

где Qs – унитарная, а Ls – нижняя треугольная матрица. Такой алгоритм носит название QL–алгоритма.
В общем случае, когда все собственные
значения матрицы различны, последовательность матриц Asимеет пределом нижнюю треугольную матрицу 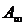 А,
расположенные в порядке возрастания их модулей. Если матрица А имеет кратные собственные значения, то
предельная матрица не является треугольной, а содержит диагональные блоки
порядка p, соответствующие
собственному числу
А,
расположенные в порядке возрастания их модулей. Если матрица А имеет кратные собственные значения, то
предельная матрица не является треугольной, а содержит диагональные блоки
порядка p, соответствующие
собственному числу 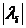 кратности p.
кратности p.
В общем случае, наддиагональныйэлемент 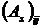 матрицы As на s-ом
шаге асимптотически равен
матрицы As на s-ом
шаге асимптотически равен 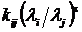 kij – постоянная
величина. Сходимость QL–алгоритма
вообще говоря недостаточна. Сходимость можно улучшить, если на каждом шаге
вместо матрицы As использовать матрицу As-ksI (QL–алгоритм со сдвигом).
Последовательность вычислений в этом случае описывается следующими
соотношениями:
kij – постоянная
величина. Сходимость QL–алгоритма
вообще говоря недостаточна. Сходимость можно улучшить, если на каждом шаге
вместо матрицы As использовать матрицу As-ksI (QL–алгоритм со сдвигом).
Последовательность вычислений в этом случае описывается следующими
соотношениями:
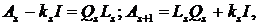
которые определяют матрицу 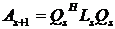
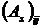 определено
соотношением
определено
соотношением 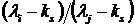
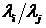 ks выбрать
близко к величине
ks выбрать
близко к величине 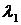 (наименьшее
собственное значение), то в пределе внедиагональные элементы первой строки
будут очень быстро стремиться к нулю. Когда ими можно пренебречь, элемент
(наименьшее
собственное значение), то в пределе внедиагональные элементы первой строки
будут очень быстро стремиться к нулю. Когда ими можно пренебречь, элемент 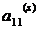 с рабочей точностью
равен
с рабочей точностью
равен 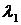 n-1-го порядка. Тогда, если QL–алгоритм
выполнен без ускорения сходимости, то все равно
n-1-го порядка. Тогда, если QL–алгоритм
выполнен без ускорения сходимости, то все равно  ks.
ks.
Если матрица А эрмитова, то очевидно, что и все матрицы Аs эрмитовы; если А действительная и симметричная, то все Qs ортогональны и все Аs действительны и симметричны.
[1] Матрица А эрмитова если она совпадает со своей комплексно сопряженной
[2] Матрица А унитарная если – сопряженная матрица.
[3] Сингулярным разложением произвольной m´n–матрицы называется разложение вида U и V – ортогональные матрицы, а S – диагональная матрица с неотрицательными диагональными элементами. Диагональные элементы S ( i=1,...,k, где k=min(m,n)) называются сингулярными числами А. Это множество чисел однозначно определяется матрицей А. Число ненулевых сингулярных чисел равно рангу А.
[4] Симметричная матрица положительно определена, если все ее собственные значения положительны. Положительно определенная матрица P обладает также тем свойством, что для всех
[5] Симметричная матрица неотрицательно определена, если все ее собственные значения неотрицательны. Такая матрица P обладает также тем свойством, что для всех mxn–матрицы А матрица симметрична и неотрицательно определена. Она положительно определена, если rankA=n.
[6] Обратной матрицей для квадратной невырожденной матрицы А называется такая матрица, для которой
[7] Матрица перестановки - это квадратная матрица, столбцы которой получаются перестановкой столбцов единичной матрицы. Матрица перестановки ортогональна.
[8]
Матрица А хессенбергова (верхняя хессенбергова) если для j [9]
Симметричная матрица А есть
трехдиагональная при для |i-j|>1.
Трехдиагональная матрица – это частный случай хесенберговой матрицы.