Методы решения систем линейных неравенств

	Загрузить архив:
	Файл: linresh.zip (111kb [zip], Скачиваний: 75) скачать

ФИНАНСОВАЯ АКАДЕМИЯ ПРИ ПРАВИТЕЛЬСТВЕ РФ

Кафедра математики и финансовых приложений

Курсовая работа

на тему:

«Методы решения систем линейных неравенств»

Выполнил студент группы МЭК 1-2

Чанкин Пётр Алексеевич

Научный руководитель:

Профессор Александр Самуилович Солодовников

Москва 2002г

Оглавление

Вступление.. PAGEREF _Toc9087427 h 2

Графический метод.. PAGEREF _Toc9087428 h 3

Симплекс-метод.. PAGEREF _Toc9087429 h 6

Метод искусственного базиса.. PAGEREF _Toc9087430 h 8

Принцип двойственности.. PAGEREF _Toc9087431 h 10

Список использованной литературы... PAGEREF _Toc9087432 h 12

[1]. Если при таком перемещении линии уровня существует некоторая точка X– первая общая точка области допустимых решений (многогранник ABCDE) и линии уровня, то f(X)- минимум fна множестве ABCDE. Если X- последняя точка пересечения линии уровня и множества ABCDE то f(X)- максимум на множестве допустимых решений. Если при а→-∞ прямая f=aпересекает множество допустимых решений, то min(f)= -∞. Если это происходит при а→+∞, то

max(f)=+∞.

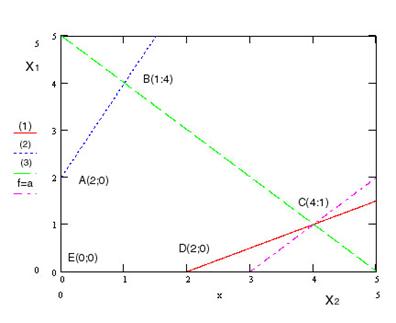
В нашем примере прямая f=aпересевает область ABCDEв точке С(4;1). Поскольку это последняя точка пересечения, max(f)=f(C)=f(4;1)=19.

[2] (столбец 3) и составляем для положительных элементов данного столбца отношения свободныйчлен/коэффициент (1/1; 2/1)[3]. Из данных отношений выбираем наименьшее и помечаем соответствующую строку[4].

Нами выбран элемент в ячейке (3;3). Теперь с помощью метода Гаусса обнуляем другие коэффициенты в данном столбце, это приводит к смене базиса и мы на один шаг приближаемся к оптимальному решению.

Б	X1	X2	X3	X4	X5	C
X3	0	0	1	1	0	2
X1	1	-1	0	1	0	1
X5	0	2	0	-1	1	1
f	0	1	0	6	0	9

Как видно из таблицы теперь все коэффициенты в последней строке больше либо равны нулю. Это означает, что нами найдено оптимальное значение. Свободные неизвестные равны нулю, значению базисных неизвестных и максимуму функции f соответствует значения свободных неизвестных.

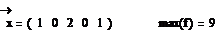
[1]Вектор нормали имеет координаты (С1;С2), где C1 и C2 коэффициенты при неизвестных в целевой функции f=C1◦X1+C2◦X2+C0.

[2]при нахождении минимума выбираем положительные коэффициенты

[3]Если положительных элементов не оказалось то данная ЗЛП не имеет решения, т.е max(f)=+∞ (при задаче на нахождение максимума) или min(f)=- ∞ (нахождение минимума)

[4]Если есть несколько одинаковых отношений можно выбрать любую строку