Определение риска и эффективности каждой из стратегий развития фирмы
| Разделы | Экономико-математическое моделирование |
| Тип | |
| Формат |
|
| Язык | Украинский |
| Загрузить архив: | |
| Файл: ref-13146.zip (173kb [zip], Скачиваний: 105) скачать |
Завдання № 1.
· Умова
Фірма планує розвиток економічної діяльності, який можливий за шістьма стратегіями. Зовнішньоекономічні умови, які будуть впливати на показники ефективності кожної стратегії мають певні ймовірності настання. Виграші при реалізації кожної стратегії та ймовірності зовнішньоекономічних умов приведеш в таблиці.
|
S |
Прибуток за з/е умов |
||||
|
1 |
2 |
3 |
4 |
5 |
|
|
S1 |
17 |
5 |
24 |
10 |
4 |
|
S2 |
11 |
20 |
14 |
32 |
46 |
|
S3 |
35 |
5 |
3 |
37 |
2 |
|
S4 |
15 |
14 |
10 |
30 |
6 |
|
S5 |
17 |
23 |
20 |
9 |
12 |
|
S6 |
19 |
4 |
16 |
2 |
1 |
|
РІ |
0.64 |
0.18 |
0.05 |
0.08 |
0.05 |
* Необхідно визначити ефективність та ризикованість кожної стратегій розвитку фірми та зробити висновок, в яку стратегію доцільно вкладати кошти і чому.
1.Щоб оцінити ефективність кожної стратегії необхідно розрахувати її середню ефективність:

( і = № стратегії,j - номер зовнішньоекономічноїумови,aij– прибуток який може отримати фірма віді- стратегії за j- умов).
|
S |
Прибуток за з/е умов |
|||||
|
1 |
2 |
3 |
4 |
5 |
Mi |
|
|
S1 |
17 |
5 |
24 |
10 |
4 |
14 |
|
S2 |
11 |
20 |
14 |
32 |
46 |
16,2 |
|
S3 |
35 |
5 |
3 |
37 |
2 |
26,5 |
|
S4 |
15 |
14 |
10 |
30 |
6 |
15,3 |
|
S5 |
17 |
23 |
20 |
9 |
12 |
17,3 |
|
S6 |
19 |
4 |
16 |
2 |
1 |
13,9 |
Так як ми знаємо, що чим більша середня ефективність стратегії тим вигіднішою є стратегія.
То за таблицею бачимо що: стратегія 5; має найбільшу середню ефективність, тобто за цим показником вищезгадана стратегія є найвигіднішою, а стратегії № 1; 2; 3; 4; 6; є найменш ефективними.
2. Оцінимо кількісну оцінку ризикованості кожної стратегії на основі показників варіації:
 а)за дисперсією:
а)за дисперсією:
Di – дисперсія,
|
S |
Прибуток за з/е умов |
|||||
|
1 |
2 |
3 |
4 |
5 |
Di |
|
|
S1 |
17 |
5 |
24 |
10 |
4 |
31,620 |
|
S2 |
11 |
20 |
14 |
32 |
46 |
84,520 |
|
S3 |
35 |
5 |
3 |
37 |
2 |
195,890 |
|
S4 |
15 |
14 |
10 |
30 |
6 |
23,378 |
|
S5 |
17 |
23 |
20 |
9 |
12 |
13,184 |
|
S6 |
19 |
4 |
16 |
2 |
1 |
54,158 |
Знаємо, що чим більша дисперсія тим більше ризик яким володіє стратегія, виходячи з цього маємо що: стратегія № 5 володіє меншим ризиком ніж стратегії № 1; 2; 3; 4; 6; тобто за цим показником 5стратегія є вигіднішою.
 |
б) розрахуємо ризик на основі стандартного відхилення:(сигма)
|
S |
Прибуток за з/е умов |
|||||
|
1 |
2 |
3 |
4 |
5 |
di |
|
|
S1 |
17 |
5 |
24 |
10 |
4 |
5,623 |
|
S2 |
11 |
20 |
14 |
32 |
46 |
9,193 |
|
S3 |
35 |
5 |
3 |
37 |
2 |
13,996 |
|
S4 |
15 |
14 |
10 |
30 |
6 |
4,835 |
|
S5 |
17 |
23 |
20 |
9 |
12 |
3,631 |
|
S6 |
19 |
4 |
16 |
2 |
1 |
7,359 |
Сигма – це середнє лінійне відхилення від фактичного значення прибутку, показник мобільності ефективності (в світовій літературі – ризик). Звідси чим менше сигма, тим надійнішою є стратегія. Тоді за цим показником вигіднішою є 5 – стратегія.
в) за коефіцієнтом варіації:

|
S |
Прибуток за з/е умов |
|||||
|
1 |
2 |
3 |
4 |
5 |
Ki var |
|
|
S1 |
17 |
5 |
24 |
10 |
4 |
0,402 |
S2 |
11 |
20 |
14 |
32 |
46 |
0,567 |
|
S3 |
35 |
5 |
3 |
37 |
2 |
0,528 |
|
S4 |
15 |
14 |
10 |
30 |
6 |
0,316 |
|
S5 |
17 |
23 |
20 |
9 |
12 |
0,209 |
|
S6 |
19 |
4 |
16 |
2 |
1 |
0,530 |
Знаємо, що чим більше значення коефіцієнта варіації, тим більш ризикованою і менш ефективною є стратегія. За цим показником вигіднішою є 5 стратегія.
г) за семі варіацією:
|
S |
Прибуток за з/е умов |
||||||
|
1 |
2 |
3 |
4 |
5 |
S+var |
S-var |
|
|
S1 |
17 |
5 |
24 |
10 |
4 |
15,73 |
66,98 |
|
S2 |
11 |
20 |
14 |
32 |
46 |
216,04 |
25,43 |
|
S3 |
35 |
5 |
3 |
37 |
2 |
12,23 |
503,41 |
|
S4 |
15 |
14 |
10 |
30 |
6 |
215,50 |
21,69 |
|
S5 |
17 |
23 |
20 |
9 |
12 |
26,61 |
9,17 |
|
S6 |
19 |
4 |
16 |
2 |
1 |
24,54 |
120,08 |
Додатня семіваріація (S+var)характеризує середні квадратичні відхилення тих значень прибутку які більші за нього. Тобто чим більше значеннявона має, тим більшим є очікуваний від стратегії прибуток. Тут вигіднішою є2 стратегія.
Від¢ємна семіваріація (S-var) характеризує середні квадратичні відхилення тих значень прибутку які менші за нього. Тобто чим меньше від’ємна семіваріація тим менше очікувані втрати. За цим показникомвигіднішою є 5 стратегія.
д) за семіквадратичним відхиленням:
|
S |
Прибуток за з/е умов |
||||||
|
1 |
2 |
3 |
4 |
5 |
SS+var |
SS-var |
|
|
S1 |
17 |
5 |
24 |
10 |
4 |
3,97 |
8,18 |
|
S2 |
11 |
20 |
14 |
32 |
46 |
14,70 |
5,04 |
|
S3 |
35 |
5 |
3 |
37 |
2 |
3,50 |
22,44 |
|
S4 |
15 |
14 |
10 |
30 |
6 |
14,68 |
4,66 |
|
S5 |
17 |
23 |
20 |
9 |
12 |
5,16 |
3,03 |
|
S6 |
19 |
4 |
16 |
2 |
1 |
4,95 |
10,96 |
Додатне семіквадратичне відхилення характеризує відхилення абсолютного значення очікуваного прибутку (можливе збільшення прибутку), тобто чим більше додатне семіквадратичне відхилення, тим більшим може виявитись абсолютне значення фактичного очікуваного прибутку. Кращою є2 стратегія.
Від’ємне семіквадратичне відхилення характеризує відхилення абсолютного значення очікуваних втрат (можливе збільшення втрат), тобто більше значення від’ємного семіквадратичного відхилення вказує на можливість збільшення абсолютного значення очікуваних втрат. Це свідчить про перевагу 5 стратегії.
е) за коефіцієнтом ризику:
|
S |
Прибуток за з/е умов |
|||||
|
1 |
2 |
3 |
4 |
5 |
Kr |
|
|
S1 |
17 |
5 |
24 |
10 |
4 |
2,06 |
|
S2 |
11 |
20 |
14 |
32 |
46 |
0,34 |
|
S3 |
35 |
5 |
3 |
37 |
2 |
6,42 |
|
S4 |
15 |
14 |
10 |
30 |
6 |
0,32 |
|
S5 |
17 |
23 |
20 |
9 |
12 |
0,59 |
|
S6 |
19 |
4 |
16 |
2 |
1 |
2,21 |
Чим менше коефіцієнт ризику (Kr) тим менше ризик
За цим показником найвигіднішою є 4 – стратегія.
3.
Зробимо інтервальну оцінку ефективності кожної
стратегії та визначити тип
ризику кожної з
них.
Щоб визначити інтервальну оцінку ефективності необхідно розрахувати граничну похибку.
Гранична похибка характеризує граничні відхилення від запланованої.
|
S |
Прибуток за з/е умов |
|||||
|
1 |
2 |
3 |
4 |
5 |
∆i |
|
|
S1 |
17 |
5 |
24 |
10 |
4 |
15,61 |
|
S2 |
11 |
20 |
14 |
32 |
46 |
25,53 |
|
S3 |
35 |
5 |
3 |
37 |
2 |
38,86 |
|
S4 |
15 |
14 |
10 |
30 |
6 |
13,42 |
|
S5 |
17 |
23 |
20 |
9 |
12 |
10,08 |
|
S6 |
19 |
4 |
16 |
2 |
1 |
20,43 |

Чим менше значення граничної похибки (граничного відхилення), тим безпечнішою і надійнішою є стратегія. Такою є 5 стратегія.
Додавши та віднявши граничну похибку до середньої ефективності отримаємо граничні межі, в яких буде коливатися фактичний прибуток по кожній стратегії.
|
S |
Прибуток за з/е умов |
||||||
|
1 |
2 |
3 |
4 |
5 |
aimax |
aimin |
|
|
S1 |
17 |
5 |
24 |
10 |
4 |
29,59 |
-1,63 |
|
S2 |
11 |
20 |
14 |
32 |
46 |
41,73 |
-9,33 |
|
S3 |
35 |
5 |
3 |
37 |
2 |
65,37 |
-12,35 |
|
S4 |
15 |
14 |
10 |
30 |
6 |
28,74 |
1,90 |
|
S5 |
17 |
23 |
20 |
9 |
12 |
27,42 |
7,26 |
|
S6 |
19 |
4 |
16 |
2 |
1 |
34,32 |
-6,54 |
За цією таблицею ми можемо бачити зміни граничних інтервалів ефективності стратегій:
aimaxхарактеризує максимальну границю інтервалу ефективності, тобто очікувані прибутки. Тут кращою є 3стратегія.
aiminхарактеризує мінімальне значення інтервалу ефективності, якщо воно є від’ємним тоді ми можемо бачити розмір втрат, виходячи з цього вигіднішою є 5 стратегія, так як вона є не збитковою і має найбільше додатне значення.
- Визначимо ризик на основі розмаху варіації:

|
S |
Прибуток за з/е умов |
|||||
|
1 |
2 |
3 |
4 |
5 |
Rivar |
|
|
S1 |
17 |
5 |
24 |
10 |
4 |
31,22 |
|
S2 |
11 |
20 |
14 |
32 |
46 |
51,05 |
|
S3 |
35 |
5 |
3 |
37 |
2 |
77,72 |
|
S4 |
15 |
14 |
10 |
30 |
6 |
26,85 |
|
S5 |
17 |
23 |
20 |
9 |
12 |
20,16 |
|
S6 |
19 |
4 |
16 |
2 |
1 |
40,86 |
Чим більше розмах варіації тим більшим ризиком володіє стратегія.
Значить стратегія №5 є найменш ризикованою.
Для того, щоб простежити динаміку стратегій зобразимо графічно три останні показники



- Встановимо тип ризику. Для цього підрахуємо відсоток втрат для кожної стратегії.
|
S |
Прибуток за з/е умов |
||||||
|
1 |
2 |
3 |
4 |
5 |
% |
Супінь ризику |
|
|
S1 |
17 |
5 |
24 |
10 |
4 |
-11,68 |
Допустимий |
|
S2 |
11 |
20 |
14 |
32 |
46 |
-57,56 |
Критичний |
|
S3 |
35 |
5 |
3 |
37 |
2 |
-46,58 |
Допустимий |
|
S4 |
15 |
14 |
10 |
30 |
6 |
12,3744 |
Ризик допустимий |
|
S5 |
17 |
23 |
20 |
9 |
12 |
41,861 |
Ризикдопустимий |
|
S6 |
19 |
4 |
16 |
2 |
1 |
-47,1 |
Допустимий |
- Висновок:
За вище наведеною таблицею ми бачимо, що:
- Стратегія №1 принесе збитки в розмірі 11,68% .
Ця стратегія збиткова, але ризик – допустимий.
- Стратегія №2 принесе збитки в розмірі 57,56%.
Ця стратегія збиткова,ризик – Критичний.
- Стратегія №3 принесе збитки в розмірі 46,58%.
Ця стратегія збиткова, але ризик – допустимий.
- Стратегія №4 принесе прибуток в розмірі 12,374%.
Стратегія є прибутковою.
- Стратегія №5 принесе прибуток в розмірі 41.861%.
Це прибуткова стратегія, яка є найвигіднішою за всіма показниками.
- Стратегія №6 принесе збитки в розмірі 47,1%.
Ця стратегія збиткова, але ризик – допустимий.
4.Побудувати матрицю ризиків:

bj– максимальне значення прибутку за реалізації кожної умови.
|
18 |
18 |
0 |
27 |
42 |
|
24 |
3 |
10 |
5 |
0 |
|
0 |
18 |
21 |
0 |
44 |
|
20 |
9 |
14 |
7 |
40 |
|
18 |
0 |
4 |
28 |
34 |
|
16 |
19 |
8 |
35 |
45 |
r=
5.
Розрахувати систему статистичних критеріїв ефективності та ризикованості
рішень:
· Розрахуємо критерій Байеса (К1):

|
S |
K1 |
|
S1 |
13,98 |
|
S2 |
16,2 |
|
S3 |
26,51 |
|
S4 |
15,32 |
|
S5 |
17,34 |
|
S6 |
13,89 |
Чим більше значення критерію К1, тим ефективнішою є стратегія. За цим показником кращою є стратегія №3.
· Критерій мінімального ризику (К2):

S |
K2 |
S1 |
19,02 |
|
S2 |
16,8 |
|
S3 |
6,49 |
|
S4 |
17,68 |
|
S5 |
15,66 |
|
S6 |
19,11 |
Критерій (К2) характеризує мінімальний ступень ризику, тобто чим менше (К2), тим меншим ризиком володіє стратегія. За цим критерієм кращою є стратегія №3.
· Критерій Гурвіца:
1. для виграшів (К3):

l - параметр впевненості інвестора щодо отримання максимального виграшу (від 0 до 1)
|
S |
0 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1 |
|
K7 |
K3 |
K5 |
K3 |
K9 |
|||||||
|
S1 |
4 |
6 |
8 |
10 |
12 |
14 |
16 |
18 |
20 |
22 |
24 |
|
S2 |
11 |
14,5 |
18 |
21,5 |
25 |
28,5 |
32 |
35,5 |
39 |
42,5 |
46 |
|
S3 |
2 |
5,5 |
9 |
12,5 |
16 |
19,5 |
23 |
26,5 |
30 |
33,5 |
37 |
|
S4 |
6 |
8,4 |
10,8 |
13,2 |
15,6 |
18 |
20,4 |
22,8 |
25,2 |
27,6 |
30 |
|
S5 |
9 |
10,4 |
11,8 |
13,2 |
14,6 |
16 |
17,4 |
18,8 |
20,2 |
21,6 |
23 |
|
S6 |
1 |
2,8 |
4,6 |
6,4 |
8,2 |
10 |
11,8 |
13,6 |
15,4 |
17,2 |
19 |
За цим показником бачимо, що вигіднішою є стратегія №2.
2. для ризиків (К4):
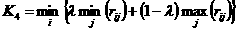
|
S |
0 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1 |
|
K8 |
K4 |
K6 |
K4 |
K10 |
|||||||
|
S1 |
42 |
37,8 |
33,6 |
29,4 |
25,2 |
21 |
16,8 |
12,6 |
8,4 |
4,2 |
0 |
|
S2 |
24 |
21,6 |
19,2 |
16,8 |
14,4 |
12 |
9,6 |
7,2 |
4,8 |
2,4 |
0 |
|
S3 |
44 |
39,6 |
35,2 |
30,8 |
26,4 |
22 |
17,6 |
13,2 |
8,8 |
4,4 |
0 |
|
S4 |
40 |
36,7 |
33,4 |
30,1 |
26,8 |
23,5 |
20,2 |
16,9 |
13,6 |
10,3 |
7 |
|
S5 |
34 |
30,6 |
27,2 |
23,8 |
20,4 |
17 |
13,6 |
10,2 |
6,8 |
3,4 |
0 |
|
S6 |
45 |
41,3 |
37,6 |
33,9 |
30,2 |
26,5 |
22,8 |
19,1 |
15,4 |
11,7 |
8 |
За цим показником найменш ризикованою є стратегія №2.
· Критерій компромісу (К5), (К6):

|
|
|
|
S |
K5 |
|
S1 |
14 |
|
S2 |
28,5 |
|
S3 |
19,5 |
|
S4 |
18 |
|
S5 |
16 |
|
S6 |
10 |
Критерій К5 вказує на те, шо стратегія №2 є найбільш ефективною.

|
l = 0,5 |
|
|
S |
K6 |
|
S1 |
21 |
|
S2 |
12 |
|
S3 |
22 |
|
S4 |
23,5 |
|
S5 |
17 |
|
S6 |
26,5 |
Критерій К6 вказує на те, що стратегія №2 є менш ризикованою, тобто вона передбачає найменші очікувані збитки.
· Критерій крайнього оптимізму (К7), (К8):
Для матриці виграшів:

|
l = 0 |
|
|
S |
K7 |
|
S1 |
4 |
|
S2 |
11 |
|
S3 |
2 |
|
S4 |
6 |
|
S5 |
9 |
|
S6 |
1 |
За цим критерієм найефективнішою є стратегія №2, так як вона вказує на найбільший очікуваний прибуток.
Для матриці ризиків:

|
l = 0 |
|
|
S |
K8 |
|
S1 |
42 |
|
S2 |
24 |
|
S3 |
44 |
|
S4 |
40 |
|
S5 |
34 |
|
S6 |
45 |
За цим критерієм найменш ризикованою є стратегія №2, так як передбачає найменші очікувані збитки.
· Критерій Ходжена-Лємана (К9), (К10):
Для матриці виграшів:

|
l = 1 |
|
|
S |
K9 |
|
S1 |
24 |
|
S2 |
46 |
|
S3 |
37 |
|
S4 |
30 |
|
S5 |
23 |
|
S6 |
19 |
Знаємо що чим більше значення даного критерію, тим більше можливе значення очікуваного прибутку, значить за цим показником кращою є стратегія №2.
Для матриці ризиків:

|
l = 1 |
|
|
S |
K10 |
|
S1 |
0 |
|
S2 |
0 |
S3 |
0 |
|
S4 |
7 |
S5 |
0 |
|
S6 |
8 |
Цей критерій характеризує очікувані втрати, значить чим менше значення К10, тим краща стратегія. За цією таблицею бачимо, що кращими є стратегії №1; 2; 3; 5.
· Критерій Лапласа (К11), (К12):
Критерій Лапласа дає змогу відокремити кращу стратегію в тому випадку, якщо жодна з зовнішньоекономічних умов не має істотної переваги. В моїй задачі стратегії мають неоднакові ймовірності, тому цей критерій не є вирішальним для вибору кращої стратегії, а лише додає більшої точності розрахункам.
Для матриці виграшів (прибутків):

|
l = від 0 до 1 |
|||||||||||
|
S |
0 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1 |
|
S1 |
4 |
4,998 |
5,996 |
6,994 |
7,992 |
8,99 |
9,988 |
10,986 |
11,984 |
12,982 |
13,98 |
|
S2 |
11 |
11,52 |
12,04 |
12,56 |
13,08 |
13,6 |
14,12 |
14,64 |
15,16 |
15,68 |
16,2 |
|
S3 |
2 |
4,451 |
6,902 |
9,353 |
11,804 |
14,255 |
16,706 |
19,157 |
21,608 |
24,059 |
26,51 |
|
S4 |
6 |
6,932 |
7,864 |
8,796 |
9,728 |
10,66 |
11,592 |
12,524 |
13,456 |
14,388 |
15,32 |
|
S5 |
9 |
9,834 |
10,668 |
11,502 |
12,336 |
13,17 |
14,004 |
14,838 |
15,672 |
16,506 |
17,34 |
|
S6 |
1 |
2,289 |
3,578 |
4,867 |
6,156 |
7,445 |
8,734 |
10,023 |
11,312 |
12,601 |
13,89 |
За цією таблицею бачимо, що найприбутковішими можуть бути стратегії №2 і №3, так як значення цього критерію для цих стратегійє найбільші.
Для матриці ризиків (втрат):

|
l = від0 до 1 |
|||||||||||
|
S |
0 |
0,1 |
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,7 |
0,8 |
0,9 |
1 |
|
S1 |
42 |
39,702 |
37,404 |
35,106 |
32,808 |
30,51 |
28,212 |
25,914 |
23,616 |
21,318 |
19,02 |
|
S2 |
24 |
23,28 |
22,56 |
21,84 |
21,12 |
20,4 |
19,68 |
18,96 |
18,24 |
17,52 |
16,8 |
|
S3 |
44 |
40,249 |
36,498 |
32,747 |
28,996 |
25,245 |
21,494 |
17,743 |
13,992 |
10,241 |
6,49 |
|
S4 |
40 |
37,768 |
35,536 |
33,304 |
31,072 |
28,84 |
26,608 |
24,376 |
22,144 |
19,912 |
17,68 |
|
S5 |
34 |
32,166 |
30,332 |
28,498 |
26,664 |
24,83 |
22,996 |
21,162 |
19,328 |
17,494 |
15,66 |
|
S6 |
45 |
42,411 |
39,822 |
37,233 |
34,644 |
32,055 |
29,466 |
26,877 |
24,288 |
21,699 |
19,11 |
Знаємо, чим менше значення даного критерію тим менше можливі очікувані збитки від стратегії. Цей показник вказує на перевагу 2 і 3 стратегій.
· Критерій Вальда (К13):
Цей критерій розраховується для матриці виграшів (прибутків), значить більше його значення позитивно характеризує стратегію.
|
S |
Прибуток за з/е умов |
|||||
|
1 |
2 |
3 |
4 |
5 |
K13 |
|
|
S1 |
17 |
5 |
24 |
10 |
4 |
12 |
|
S2 |
11 |
20 |
14 |
32 |
46 |
24,6 |
|
S3 |
35 |
5 |
3 |
37 |
2 |
16,4 |
|
S4 |
15 |
14 |
10 |
30 |
6 |
15 |
|
S5 |
17 |
23 |
20 |
9 |
12 |
16,2 |
|
S6 |
19 |
4 |
16 |
2 |
1 |
8,4 |
За цим критерієм стратегія №2 є вигіднішою, тому що очікувані при ній прибутки є найбільшими.
· Критерій Севіджа (К14):
Цей критерій розраховується для матриці ризиків (втрат), тому його менше значення вказує на перевагу певної стратегії.
|
S |
Ризик за з/е умов |
|||||
|
1 |
2 |
3 |
4 |
5 |
K14 |
|
|
S1 |
18 |
18 |
0 |
27 |
42 |
21 |
|
S2 |
24 |
3 |
10 |
5 |
0 |
8,4 |
|
S3 |
0 |
18 |
21 |
0 |
44 |
16,6 |
|
S4 |
20 |
9 |
14 |
7 |
40 |
18 |
|
S5 |
18 |
0 |
4 |
28 |
34 |
16,8 |
|
S6 |
16 |
19 |
8 |
35 |
45 |
24,6 |
За цим критерієм стратегія №2 переважає, тому що очікувані при ній збитки є найменшими.
· Висновок:
Для того щоб визначити яку із стратегій для фірми доцільно фінансувати
проаналізуємо всі кількісні характеристики рівня ефективності та ризикованості стратегій, тобто оцінимо стратегії за отриманими критеріями.
Для полегшення цієї задачі відобразимо отримані результати в таблиці.
|
K1 |
K2 |
K3 |
K4 |
K5 |
K6 |
K7 |
K8 |
K9 |
K10 |
K11 |
K12 |
K13 |
K14 |
|
S3 |
S3 |
S2 |
S2 |
S2 |
S2 |
S2 |
S2 |
S2 |
S1 |
S3 |
S2 |
S2 |
S2 |
|
S2 |
S2 |
S3 |
|||||||||||
|
S3 |
|||||||||||||
|
S5 |
· Тепер відобразимо частоту появи кожної стратегії:
|
S1 |
1 |
|
S2 |
12 |
|
S3 |
5 |
|
S4 |
0 |
|
S5 |
1 |
|
S6 |
0 |
Робимо висновок, що за критеріями від К1 до К14 кращою з стратегій є стратегія №2, тобто саме цю стратегію рекомендую обрати фірмі для інвестування.
 l = 0,5
l = 0,5