Высшая математика, интегралы (шпаргалка)
| Загрузить архив: | |
| Файл: ref-13714.zip (116kb [zip], Скачиваний: 380) скачать |
Равномерная непрерывность
Определение 28.7: Функция  равномерно
непрерывной на множестве
равномерно
непрерывной на множестве 


Пояснение:  Пусть:
Пусть: 
 Т.е. функция
Т.е. функция  не
является равномерно непрерывной на множестве
не
является равномерно непрерывной на множестве 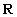
Теорема 28.3: Непрерывная на отрезке функция – равномерно непрерывна на нём.
Классы интегрируемых функций
Теорема 28.4: Непрерывная на отрезке функция – интегрируема на нём.
Теорема 28.5: Монотонная на отрезке функция – интегрируема на нём.
Теорема 28.5: Если функция 
 , и если
, и если 
 Причём общая длина этих
интервалов меньше
Причём общая длина этих
интервалов меньше 

 .
.
Замечание: Очевидно, что
если 




 и
и 
Существование первообразной
Определение 28.9: Пусть 





 переменным
верхним пределом, аналогично функция
переменным
верхним пределом, аналогично функция  переменным нижним
пределом.
переменным нижним
пределом.
Теорема 28.6: Если функция 




Замечание 1: Из дифференцируемости
функции 

Замечание 2: Поскольку 


Интегрирование подстановкой
Пусть для вычисления интеграла 

Теорема. Если 1. Функция 


2. множеством значений функции  при
при  a;b]
a;b]
3. 


Док-во: Пусть F(x) есть первообразная для f(x) на
отрезке [a;b]. Тогда по формуле
Ньютона-Лейбница 








Формула замены переменной в определенном интеграле.
1. при вычислении опред. интег-ла методом подстановки возвращаться к старой переменной не требуется;
2.
часто вместо подстановки  t=g(x)
t=g(x)
3. не следует забывать менять пределы интегрирования при замене переменных.
Интегрирование заменой переменной.
а). Метод подведения под знак дифференциала
Пусть
требуется вычислить интеграл 




Тогда:




Пример: Вычислить 

Подстановка:

б). Метод подстановки
Пусть
требуется вычислить интеграл 












Пример: Вычислить 


Интегрирование
по частям. Пусть 





Пример: Вычислить 
Положим








Замечание 26.5: Иногда
при вычислении интеграла 


Интегрирование рациональных функций
Постановка задачи:


|
1).
|
2).
|
|
3).
|
т.е. все задачи сводятся к задаче B.2).
Теорема 1:Пусть 




|
1.
|
2.
|
3.
|
4.
|
5.
|
|
6.
|
7.
|
8.
|
9.
|
10.
|
Интегрирования дробно-линейных и квадратичных иррациональностей

Сделав
подстановку: 

тогда


a). Подстановки Эйлера.
1).
Корни многочлена 


2).
Корни многочлена 



b). Подстановка: 
|
1).
|
2).
|
|
3).
|
c).
Если


Интегрирование функций, рационально зависящих от тригонометрических

Универсальная
подстановка: 





Интегрируется по частям
Неопределенный интеграл
Определение 26.1: Функция  первообразной
для функции
первообразной
для функции 


Пусть





Определение 26.2: Неопределённым интегралом от функции 



Замечание 26.1: Если 



Замечание 26.2:Подынтегральное выражение в
определении представляет из себя полный дифференциал первообразной 


Замечание 26.3:Два неопределённых интеграла равны “с точностью до постоянной”.
Св-ва неопределенного интеграла:
1.Дифференциал от неопределенного интеграла равен подынтегральному выражению, а производная неопред. интегр. равна подынтегр. функции. Благодаря этому св-ву правильность интегрирования проверяется дифференцированием.


2. Неопред. интегр. от дифференциала нек-рой функции равен сумме этой функции и производной постоянной:

3. Постоянный множитель м. выносить за знак интеграла:
 a
a 0-постоянная.
0-постоянная.
4. Неопред. интегр. от алгебраич. суммы конечного числа непрерывных функций равен алгебраич. сумме интегралов от слагаемых функций:

5.
(Инвариантность формулы интегрирования). Если
 u=
u=
Табличные интегралы
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определённый интеграл.
Интегрируемость
Определение 28.1: Множество точек отрезка 
 разбиением
отрезка
разбиением
отрезка  Длины частичных
отрезков разбиения обозначим:
Длины частичных
отрезков разбиения обозначим:  Мелкостью разбиения
Мелкостью разбиения


Определение 28.2: Пусть в определении 28.1 для всех 
 Интегральной суммой
функции
Интегральной суммой
функции 
 с разбиением
с разбиением 



Определение 28.3: Пределом интегральных сумм функции 
 назовём такое число
назовём такое число 



Определение 28.4: Функция  интегрируемой на
отрезке
интегрируемой на
отрезке  , если существует конечный
предел её интегнральных сумм на
, если существует конечный
предел её интегнральных сумм на  . Обозначается:
. Обозначается: 
Теорема 28.1: Если 
 , то она ограничена на нём.
, то она ограничена на нём.
Замечание 1: Эта теорема является необходимым, но недостаточным условием интегрируемости функции. Пример – функция Дирихле (ограничена, но неинтегрируема).
Критерий интегрируемости функций
Теорема 28.2: Для того, чтобы ограниченная на некотором отрезке
функция, была интегрируема на нём, необходимо и достаточно, чтобы выполнялось
условие: 
Следствие 1: Условие Т.2
эквивалентно условию: 
Следствие 2: Если функция интегрируема на , то: 
Определение 28.8: Определённым интегралом функции 
 называется число
называется число 

 . Условие интегрируемости эквивалентно
существованию определённого интеграла.
. Условие интегрируемости эквивалентно
существованию определённого интеграла.
Свойства определённого интеграла
1.
Если с – постоянное число и функция f(x) интегрируема на [a;b], то  с можно выносить за знак
определенного интег-ла.
с можно выносить за знак
определенного интег-ла.
2. Если функции f(x), g(x) интегрируемы на [a;b], тогда интегрируема на [a;b] их сумма и разность


3.
Если 

4.
Если функция f(x) интегрируема на [a;b] и a Сравнение определённых интегралов Если
Если
Неравенство
му непрерывными функциями на отрезке [a;b], можно интегрировать. Если
Модуль
определенного интег-ла не превосходит интег-ла от модуля подынтегральной
функции. Если Оценка
интеграла. Если m и M-соответственно наименьшее и
наибольшее значения функции y=f(x)на отрезке [a;b]. Если Если
функция f(x) непрерывна на отрезке [a;b], то
существует точка Док-во:
По формуле Ньютона-Лейбница имеем Эта
теорема при f(x) Число Если
Док-во:
Рассмотрим тождество Преобразуем
каждую разность в скобках по формуле Лагранжа Переходя
к пределу при = интеграл с переменным верхним пределом Если
изменять, например, верхний предел так, чтобы не выйти за пределы отрезка [a;b], то
величина интеграла будет изменяться. Другими словами, интеграл с переменным
верхним пределом представляет собой функцию своего верхнего предела.
Производная определенного интег-ла по переменному верхнему пределу равна
подынтегральной функции, в к-рой переменная интегрирования заменена этим
пределом, т.е. Док-во:
По формуле Ньютона-Лейбница имеем: Следовательно,
= Это
значит, что определенный интег-л с переменным верхним пределом есть одна из
первообразных подынтегральной функции.  аддивностью определенного
интеграла.
аддивностью определенного
интеграла.





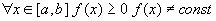















Теорема о среднем значении
 такая, что
такая, что 
 F’(x)=f(x). Применяя к разности F(b)-F(a)
теорему Лагранжа (теорему о конечном приращении функции), получим F(b)-F(a)=F’(c)*(b-a)=f(c)*(b-a).
F’(x)=f(x). Применяя к разности F(b)-F(a)
теорему Лагранжа (теорему о конечном приращении функции), получим F(b)-F(a)=F’(c)*(b-a)=f(c)*(b-a).
 f(с) и основанием b-a.
f(с) и основанием b-a. наз-ся средним
значением функции f(x) на отрезке [a;b].
наз-ся средним
значением функции f(x) на отрезке [a;b].Формула Ньютона-Лейбница









 y=f(x) непрерывна на [a;b].
Поэтому существует предел интегральной суммы, равный определенному интегралу от
f(x) на [a;b].
y=f(x) непрерывна на [a;b].
Поэтому существует предел интегральной суммы, равный определенному интегралу от
f(x) на [a;b]. F(b)-F(a)=
F(b)-F(a)= ,
т.е.
,
т.е. 

























































