Гамма функции
| Загрузить архив: | |
| Файл: ref-13921.zip (129kb [zip], Скачиваний: 158) скачать |
1.Бэта-функции 6
Бэта – функции определяются интегралом Эйлера первого рода:



 (1.1)
(1.1)
сходятся при 


 =
=
т.e. аргумент  и
и 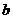 входят в
входят в  симетрично. Принимая
во внимание тождество
симетрично. Принимая
во внимание тождество

по формуле интегрирования почестям имеем
Откуда

 (1.2)
(1.2)
7
При целом b = n последовательно применяя(1.2)
Получим
 (1.3)
(1.3)
при целых  = m,
= m,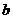 = n,имеем
= n,имеем

но B(1,1) = 1,следовательно:



Положим
в (1.1)  .Так как
график функции
.Так как
график функции 

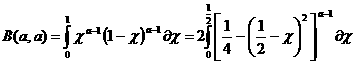
8
и в результате подстановки

полагая в(1.1) 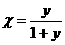 ,откуда
,откуда 
 (1.4)
(1.4)
разделяя интеграл на два в пределах
от 0 до 1 иот 1 до  и применение ко
второму интегралу подстановки
и применение ко
второму интегралу подстановки 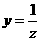


2.Гамма-функция 9
Гамма функцию определяет интеграл Эйлера второго рода
G(a) =

 (2.1)
(2.1)
сходящийся при  0.Положим
0.Положим  ty,t > 0 ,имеем
ty,t > 0 ,имеем
G(a) =
и после замены 
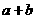 и tчерез 1+t ,получим
и tчерез 1+t ,получим

Умножая это
равенство и интегрируя по t и пределах
от 0 до , имеем:
, имеем:

или на основании (1.4) и после изменения в правой части порядка интегрирования ,получаем:

10
откуда
 (2.2)
(2.2)
заменяя в (2,1)  ,на
,на 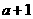 и интегрируем по
частям
и интегрируем по
частям

получаем рекурентною формулу

 (2.3)
(2.3)

так как

но при целом  имеем
имеем
 (2.4)
(2.4)
то есть при целых значениях аргумента гамма-функция превращается в факториал.Порядок которого на единицу меньше взятого значения аргумента.При n=1 в (2.4) имеем

3. Производная гамма функции 11
Интеграл


сходится
при каждом 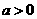


 при
при 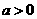
В области 

 и можна применить
признак Веерштраса. Сходящимся при всех значениях
и можна применить
признак Веерштраса. Сходящимся при всех значениях 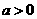 является и весь
интеграл
является и весь
интеграл  так как и второе
слогаемое правой части является интегралом, заведомо сходящимся при любом
так как и второе
слогаемое правой части является интегралом, заведомо сходящимся при любом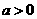

 где
где  произвольно.Действительно для всех указаных
значений
произвольно.Действительно для всех указаных
значений 




 ходится равномерно.
ходится равномерно.
Отсюда
вытекает непрерывность гамма функции при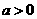
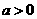 функция
функция непрерывна при
непрерывна при 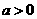 и
и

12
сходится равномерно на каждом
сегменте  ,
,  . Выберем число
. Выберем число так , чтобы
так , чтобы 
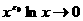 при
при 
 такое , что
такое , что 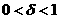 и
и  на
на
 справедливо
неравенство
справедливо
неравенство

и так как интеграл  сходится, то интеграл
сходится, то интеграл  сходится равномерно
относительно
сходится равномерно
относительно  на
на 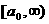
 существует такое число
существует такое число
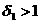
 выполняется
неравенство
выполняется
неравенство 
 и всех
и всех  получим
получим  в силу
признака сравнения следует , что интеграл
в силу
признака сравнения следует , что интеграл  сходится равномерно
относительно
сходится равномерно
относительно на
на 

в котором подынтегральная функция непрерывна в области



 интеграл
интеграл

13
сходится равномерно , а,
следовательно , гаммма функция бесконечно дифференцируема при любом 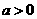 и справедливо
равенство
и справедливо
равенство


Относительно
интеграла 

По индукции
доказывается , что Г-функция бесконечно дифференцируема при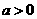

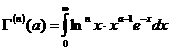
Изучим
теперь поведение 
Из
выражения для второй производной 
 для всех
для всех 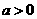
 возрастает. Поскольку
возрастает. Поскольку  [1,2]производная
[1,2]производная  при
при  и
и при
при  Монотонно
убывает на
Монотонно
убывает на 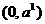




 из формулы
из формулы 
 при
при 
14
Равенство 
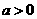


Положим для

 из (-1,0). Получаем, что так продолженная
функция
из (-1,0). Получаем, что так продолженная
функция  принимает на (-1,0)
отрицательные значения и при
принимает на (-1,0)
отрицательные значения и при 
 функция
функция 
Определив таким образом 
 той же
формуле продолжить ее на интервал (-2,-1). На этом интервале продолжением
той же
формуле продолжить ее на интервал (-2,-1). На этом интервале продолжением  окажется функция,
принимающая положительные значения и такая, что
окажется функция,
принимающая положительные значения и такая, что 
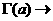

 и
и 


Отметим еще раз, что интеграл

определяет
Г-функцию только при положительных значениях 



15

(рис.1)
4. Вычисление некоторых интегралов. 16
Формула Стирлинга
Применим гамма функцию к вычислению интеграла:

где m > -1,n > -1.Полагая , что 


и на основании (2.2) имеем
 (3.1)
(3.1)
В интеграле

Где k > -1,n >
0,достаточно положить 


17
Интеграл

Где s > 0,разложить в ряд



=
где 
Рассмотрим неполные гамма функции (функции Прима)

связанные неравенством


Разлагая, в ряд имеем
в ряд имеем

18

Переходя к выводу формулы Стирлинга , дающей в частностиприближенное значениеn! при больших значениях n ,рассмотрим предварительно вспомогательную функцию
 (3.2)
(3.2)
Непрерывна на интервале (-1,
 до
до при изменении
при изменении от
от  до
до и обращаются в 0при u = 0.Так
как
и обращаются в 0при u = 0.Так
как

то
 u > 0
и при u < 0 , далее имеем
u > 0
и при u < 0 , далее имеем

И так производная непрерывна и положительна
во всем интервале 
19

Из предыдущего следует, что существует
обратная функция,  определенная на
интервале
определенная на
интервале  непрерывная и
монотонно возрастающая в этом интервале,
непрерывная и
монотонно возрастающая в этом интервале,
Обращающаяся в 0 при v=0 и удовлетворяющая условие

 (3.3)
(3.3)
Формулу Стирлинга выведем из равенства
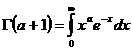
полагая 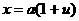

Положим далее  u = -1при
u = -1при 
 при
при  .Замечая что(см.3.2)
.Замечая что(см.3.2)

20
имеем
 ,
,
полагая на конец ,

или

в пределе при 


откуда вытекает формула Стирлинга

которую можно взять в виде
21
 (3.4)
(3.4)
где  ,при
,при 

для достаточно больших  полагают
полагают
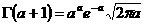 (3.5)
(3.5)
вычисление же производится при помощи логарифмов

если  целое положительное
число, то
целое положительное
число, то  и (3.5) превращается в
приближенную формулу вычисления факториалов при больших значениях n
и (3.5) превращается в
приближенную формулу вычисления факториалов при больших значениях n
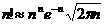
приведем без вывода более точную формулу
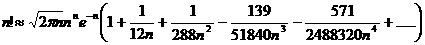
где в скобках стоит не сходящийся ряд.
5. Примеры вычисления интегралов 22
Для вычисления необходимы формулы:


Г(

Вычислить интегралы





23

Міністерство освіти і науки України
Запорізький державний університет
ДО ЗАХИСТУ ДОПУЩЕНИЙ
Зав. каф. Математичного аналізу
д. т. н. проф. ____ С.Ф. Шишканова
_________________________ 2002р.
ПОЯСНЮВАЛЬНА ЗАПИСКА ДО КУРСОВОГО ПРОЕКТУ
ГАМА ФУНКЦІЇ
Розробив
Ст..гр.. 8221-2
Садигов Р.А.
Керівник
Ст. викладач
Кудря В.І.
Запоріжжя 2002.
Содержание
Задание на курсовую работу........................... ...................................2
Реферат............................................................. ...................................4
введение............................................................ ...................................5
1. Бета функции……………………………………………..............6
2. Гамма функции....................................... ...................................9
3. Производная гаммафункции ............... ..................................11
4. Вычисление интегралов формула Стирлинга............................16
5. Примеры вычеслений............................. ..................................22
вывод................................................................ ..................................24
Список литературы……………………………………………..............25
Реферат
Курсовая работа: 24 ст., 5 источников, 1 рис.
Обьект иследований: гамма и ее приложения.
В работе идет речь о представлении бета и гамма функций с помощью интегралов Эйлера соответствено первого и второго рода. И о их применении для вычисления интегралов.
Ключевые слова:
ГАММАИ БЕТА ФУНКЦИЯ, ИНТЕГРАЛ ЭЙЛЕРА, ПРОИЗВОДНАЯ, ПРЕДЕЛ.
Введение
Выделяют особый класс функций, представимых в виде собственого либо несобственого интеграла, который зависит не только от формальной переменной, а и от параметра.
Такие функции называются интегралами зависящими от параметра. К их числу относятся гамма и бета функции Эйлера.
Бета функции представимы интеграломЭйлера первого рода:

гамма функция представляется интегралом Эйлера второго рода:

Вывод
Гамма функции являются удобным средством для вычисления некоторых интегралов в частности многих из тех интегралов, которые не представимы в элементарных функциях.
Благодаря этому они широко применяются в математике и ее приложениях, в механике, термодинамике и в других отраслях современной науки.
Список литературы
1.Специальные функции и их приложения:
Лебедев И.И.,М.,Гостехтериоиздат,1953
2. Математический анализ часть 2:
Ильин О.А., Садовничий В.А., Сендов Бл.Х.,М.,”Московский университет”,1987
3. Сборник задач по математическому анализу:
Демидович Б.П.,М.,Наука,1966
4. Интегралы и ряды специальные функции:
Прудников А.П., Брычков Ю.А.,М.,Наука,1983
5. Специальные функции:
Кузнецов , М.,”Высшая школа”,1965
