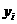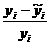Эконометрика (оценить тесноту связи между факторами при помощи коэффициентов корреляции рангов Спирмена и Кендела и другие задачи)
| Загрузить архив: | |
| Файл: ref-14981.zip (106kb [zip], Скачиваний: 98) скачать |
Московское Представительство
Ленинградского Государственного Областного Университета им. Пушкина
Индивидуальное задание
по курсу «Эконометрика»
Выполнил: Макаров А.В.
Студент 3-его курса
Группы П-31д
Дневного отделения
Преподаватель: Мезенцев Н.С.
.
Москва 2002г.
Задача 1.
При помощи коэффициентов корреляции рангов Спирмена и Кендела
оценить тесноту связи между факторами на основании следующих данных:
Табл.1
|
№ Предприятия |
Объем реализации, млн.руб. |
Затраты по маркетенгу, тыс. руб. |
Rx |
Ry |
di |
di2 |
|
1 |
12 |
462 |
2 |
1 |
1 |
1 |
|
2 |
18,8 |
939 |
5 |
5 |
0 |
0 |
|
3 |
11 |
506 |
1 |
2 |
-1 |
1 |
|
4 |
29 |
1108 |
7 |
7 |
0 |
0 |
|
5 |
17,5 |
872 |
4 |
4 |
0 |
0 |
|
6 |
23,9 |
765 |
6 |
3 |
3 |
9 |
|
7 |
35,6 |
1368 |
8 |
8 |
0 |
0 |
|
8 |
15,4 |
1002 |
3 |
6 |
-3 |
9 |
|
Итого |
20 |
1)находим коэффициент Спирмена:

 .
.
Вывод: Коэффициент Спирмена равен 0,77.
По шкале Чеддока связь между факторами сильная.
2)находим коэффициент Кендела:
|
x |
y |
Rx |
Ry |
+ |
- |
|
12,0 |
462 |
2 |
1 |
6 |
|
|
18,8 |
939 |
5 |
5 |
3 |
3 |
|
11,0 |
506 |
1 |
2 |
||
|
29,0 |
1108 |
7 |
7 |
1 |
3 |
|
17,5 |
872 |
4 |
4 |
2 |
1 |
|
23,9 |
756 |
6 |
3 |
1 |
|
|
35,6 |
1368 |
8 |
8 |
1 |
|
|
15,4 |
1002 |
3 |
6 |
||
|
P=13 |
Q= -8 |
||||
|
S=P+Q=13-8=5 |


Вывод: Коэффициент Кендела равен 0,19.
По шкале Чеддока связь между факторами слабая.
Задача 2.
Имеются исходные данные о предприятиях отрасли. Используя коэффициент конкордации, оценить тесноту связи между приведёнными в таблице факторами.
Табл.1

 =302
=302


Вывод: Коэф. Конкордации равен 0,674. По шкале Чеддока связь заметная.
Задача 4.
Построить модель связи между указанными факторами, проверить её адекватность, осуществить точечный и интервальный прогноз методом экстраполяции.
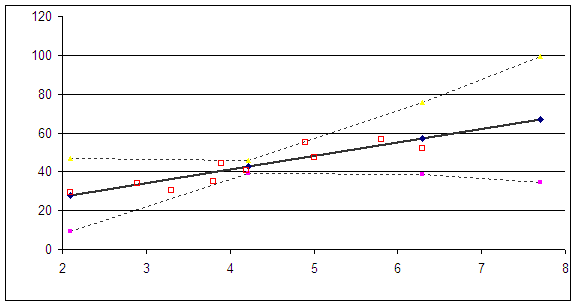
4.1. Исходные данные отложить на координатной плоскости и сделать предварительное заключение о наличии связи.
таб.1 диагр.1
|
x |
y |
|
2,1 |
29,5 |
|
2,9 |
34,2 |
|
3,3 |
30,6 |
|
3,8 |
35,2 |
|
4,2 |
40,7 |
|
3,9 |
44,5 |
|
5,0 |
47,2 |
|
4,9 |
55,2 |
|
6,3 |
51,8 |
|
5,8 |
56,7 |

Вывод: Из диаграммы 1 видно, что связь между факторами x и y
прямая сильная линейная связь.
4.2.Рассчитайте линейный коэффициент корреляции. Используя t-критерий Стьюдента, проверьте значимость коэффициента корреляции. Сделайте вывод о тесноте связи между факторами х и у, используя шкалу Чеддока.
таб.2
|
№ |
|
|
|
|
xy |
|
|
|
|
1 |
2,1 |
29,5 |
4,41 |
870,25 |
61,95 |
27,91 |
1,59 |
0,054 |
|
2 |
2,9 |
34,2 |
8,41 |
1169,64 |
99,18 |
33,46 |
0,74 |
0,022 |
|
3 |
3,3 |
30,6 |
10,89 |
936,36 |
100,98 |
36,23 |
-5,63 |
0,184 |
|
4 |
3,8 |
35,2 |
14,44 |
1239,04 |
133,76 |
39,69 |
-4,49 |
0,128 |
|
5 |
4,2 |
40,7 |
17,64 |
1656,49 |
170,94 |
42,47 |
-1,77 |
0,043 |
|
6 |
3,9 |
44,5 |
15,21 |
1980,25 |
173,55 |
40,39 |
4,11 |
0,092 |
|
7 |
5,0 |
47,2 |
25 |
2227,84 |
236 |
48,01 |
-0,81 |
0,017 |
|
8 |
4,9 |
55,2 |
24,01 |
3047,04 |
270,48 |
47,32 |
7,88 |
0,143 |
|
9 |
6,3 |
51,8 |
39,69 |
2683,24 |
326,34 |
57,02 |
-5,22 |
0,101 |
|
10 |
5,8 |
56,7 |
33,64 |
3214,89 |
328,86 |
53,55 |
3,15 |
0,056 |
|
ИТОГО: |
42,2 |
426 |
193,34 |
19025,04 |
1902,04 |
426 |
0,840 |
|
|
Среднее зн. |
4,22 |
42,56 |
19,334 |
1902,504 |
190,204 |
4.2.1.Проверим тесноту связи между факторами, рассчитаем ЛКК:


Вывод: по шкале Чеддока связь сильная.
4.2.2.Проверим статистическую значимость ЛКК по критерию Стьюдента:
1)Критерий Стьюдента: tвыб<=tкр
2)Но: r=0 tкр=2,31
tвыб=rвыб*
Вывод: таким образом поскольку tвыб=5,84 90% нулевая гипотеза отвергается, это указывает на наличие сильной линейной связи. 4.3.Полагая, что связь между факторами х и у может быть описана
линейной функцией, используя процедуру метода наименьших квадратов, запишите
систему нормальных уравнений относительно коэффициентов линейного уравнения
регрессии. Любым способом рассчитайте эти коэффициенты. Последовательно подставляя в уравнение регрессии 4.4.Для полученной модели связи между факторами Х и У
рассчитайте среднюю ошибку аппроксимации. Сделайте предварительное заключение
приемлемости полученной модели. Для расчета заполним 8-ую и 9-ую графу табл.2 Вывод: модель следует признать удовлетворительной. 4.5.
Проверьте значимость коэффициента уравнения регрессии a1 на основе t-критерия Стьюдента. № 1 2,1 29,5 27,91 2,5281 214,623 170,5636 2 2,9 34,2 33,46 0,5476 82,81 69,8896 3 3,3 30,6 36,23 31,6969 40,069 143,0416 4 3,8 35,2 39,69 20,1601 8,237 54,1696 5 4,2 40,7 42,47 3,1329 0,008 3,4596 6 3,9 44,5 40,39 16,8921 4,709 3,7636 7 5 47,2 48,01 0,6561 29,703 21,5296 8 4,9 55,2 47,32 62,0944 22,658 159,7696 9 6,3 51,8 57,02 27,2484 209,092 85,3776 10 5,8 56,7 53,55 9,9225 120,78 199,9396 ИТОГО: 42,2 425,6 426,1 174,8791 732,687 911,504 Среднее
4,22 42,56 Статистическая
проверка: 4.6.
Проверьте адекватность модели (уравнения регрессии) в целом на основе F-критерия Фишера-Снедекора. Решение: Процедура статистической проверки: Вывод: т.к. Fвыб.>Fкр.,
то с доверительной вероятностью 95% нулевая гипотеза отвергается (т.е.
принимается альтернативная). Изучаемая модель адекватна и может быть
использована для прогнозирования и принятия управленческих решений. 4.7.
Рассчитайте эмпирический коэффициент детерминации. Решение: Вывод: т.е. 80% вариации объясняется фактором включенным в
модель, а 20% не включенными в модель факторами. 4.8.
Рассчитайте корреляционное отношение. Сравните полученное значение с величиной
линейного коэффициента корреляции. Решение: Эмпирическое корреляционное отношение указывает на тесноту
связи между двумя факторами для любой связи, если связь линейная, то 4.9.
Выполните точечный прогноз для Решение: 4.10-4.12
Рассчитайте доверительные интервалы для уравнения регрессии
и для результирующего признака а) исходные данные, б) линию регрессии, в) точечный прогноз, г) 90% доверительные интервалы. Сформулируйте общий вывод относительно
полученной модели. Решение: Для выполнения интервального прогноза
рассматриваем две области. 1)для
yиз области изменения фактора xдоверительные
границы для линейного уравнения регрессии рассчитывается по формуле: 2)для
прогнозного значения Исходные данные: 1)n=10 2)t=2,31(таб.) 3) 4) 5) 6)
Таб.4 № 1 2,1 -2,12 4,49 3,03 1,74 2,31 4,68 18,81 27,91 9,10 46,72 2 4,22 0,00 0,00 0,1 0,32 2,31 4,68 3,46 42,56 39,10 46,02 3 6,3 2,08 4,33 2,93 1,71 2,31 4,68 18,49 57,02 38,53 75,51 4 7,7 3,48 12,11 9,02 3 2,31 4,68 32,43 66,72 34,29 99,15 Вывод: поскольку90% точек наблюдения попало в 90%
доверительный интервал данная модель и ее доверительные границымогут использоваться для прогнозирования с
90% доверительной вероятностью. 
 из графы (2) табл.2,
рассчитаем значенияи заполним графу (7)
табл.2
из графы (2) табл.2,
рассчитаем значенияи заполним графу (7)
табл.2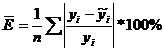




 Решение:
Таб.3
Решение:
Таб.3



 Вывод:
С доверительной вероятностью 90% коэффициент a1- статистически значим, т.е. нулевая гипотеза
отвергается.
Вывод:
С доверительной вероятностью 90% коэффициент a1- статистически значим, т.е. нулевая гипотеза
отвергается. :модель не адекватна
:модель не адекватна
 (таб. 3)
(таб. 3) -показывает
долю вариации.
-показывает
долю вариации.

 , т.е.
коэффициент ЛКК совпадает с коэффициентом детерминации.
, т.е.
коэффициент ЛКК совпадает с коэффициентом детерминации. .
.
 при доверительной вероятности
при доверительной вероятности  =90%. Изобразите
в одной системе координат:
=90%. Изобразите
в одной системе координат: -математическое ожидание среднего.
-математическое ожидание среднего.
 доверительный
интервал для
доверительный
интервал для  рассчитывается
по формуле:
рассчитывается
по формуле: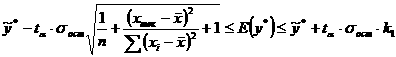


 :
27,91 42,56 57,02 66,72
:
27,91 42,56 57,02 66,72  19,334-4,222)=1,53.
19,334-4,222)=1,53.