Транспортная задача
| Загрузить архив: | |
| Файл: ref-15410.zip (46kb [zip], Скачиваний: 51) скачать |
Кавминводский Институт сервиса (КМВИС)
Филиал
Южно-Российского Государственного Университета Экономики и Сервиса (ЮРГУЭС)
Курсовая работа
по информатике
тема работы: «Транспортная задача»
Выполнил студент 2-го курса
Очного отделения группы ИС-01
Ханин Константин Александрович
проверил старший преподаватель
Макаров Борис Сергеевич.
Пятигорск 2003 г.
1.Постановка задачи.
В качестве объекта исследования рассматривается сеть с потоками однородного продукта – экономико-математическая модель задачи оптимизации транспорта энергии, газа, трубопроводных систем различного назначения, а также транспортировки продукции от поставщиков к потребителям. Требуется написать программу оптимизации транспорта энергии, газа, трубопроводных систем различного назначения по заданной схеме, решить систему уравнений заданным методом.
2. Спецификация.
2.1. Название задачи.
По заданной схеме (3):

следует найти в ходе выполнения работы направления потоков по ветвям и их величину P (в условных единицах).
2.2 Описание задачи.
Выберем произвольное направление на схеме по ветвям для формирования матрицы A:

Таким образом, получим матрицу A вида:
Таб.№1.
Ветви SHAPE* MERGEFORMAT 
|
-1 |
0 |
0 |
0 |
1 |
0 |
0 |
|
0 |
-1 |
0 |
0 |
-1 |
-1 |
0 |
|
0 |
0 |
1 |
0 |
0 |
1 |
1 |
|
0 |
0 |
0 |
1 |
0 |
0 |
-1 |
|
1 |
1 |
-1 |
-1 |
0 |
0 |
0 |
|
Узлы |
|
1 2 3 4 0 |
0-10-2 0-3 0-41-2 2-3 3-4
Затем введём диагональную матрицу R, элементами которой являются заданные стоимости перевозок по отдельным ветвям.
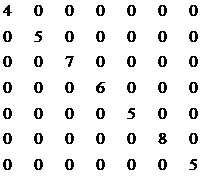
R =
Можно показать, опуская преобразования, связанные с поиском минимума целевой функции F, что искомый вектор потоков Р можно вычислить (в матричной форме) как
 = -R-1
= -R-1 t
t
 .
.
Где
R-1
– матрица, обратная матрице R,
At
– транспонированная
матрица А,  - вектор Лагранжа
(потенциалов), который предварительно должен быть найден из решения системы
уравнений в матричной форме:
- вектор Лагранжа
(потенциалов), который предварительно должен быть найден из решения системы
уравнений в матричной форме:
A -1
-1 t
t
 =
=
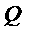 .
.
Вектор Q- объём производства в узлах схемы, которые задаются в качестве входных данных по вариантам работы, и входит в уравнение:
A +
+  = 0,
= 0,
Таблица соответствия:
|
Ветви |
Начало |
Конец |
Стоимость |
|
1 |
0 |
1 |
4 |
|
2 |
0 |
2 |
5 |
|
3 |
0 |
3 |
7 |
|
4 |
0 |
4 |
6 |
|
5 |
1 |
2 |
5 |
|
6 |
2 |
3 |
8 |
|
7 |
3 |
4 |
5 |
2.3. Управление программой.
В среде Turbo Pascal программа после подготовки текста программы можно попытаться исполнить её, т.е. откомпилировать программу, связать её (если это необходимо) с библиотекой стандартных процедур и функций, загрузить в оперативную память и передать её управление. Вся эта последовательность действий называется прогоном программы и реализуется командой Ctrl+F9 или нажатием мышкой на панели меню раздел Run и далее Run.
Если в программе нет синтаксических ошибок, то все действия выполняются последовательно одно за другим, при этом в небольшом окне сообщается о количестве откомпилированных строк и объёме доступной оперативной памяти. Перед передачей управления загруженной программе среда очищает экран (точнее, выводит на экран окно прогона программы), а после завершения работы программы вновь берёт управление компьютером на себя и восстанавливает на экран окно редактора.
Итак, нажимаем Ctrl+F9 или выбираем из меню Run+Run, появляется голубой экран, которым является оформление курсовой работы, через некоторое время на экране появляется меню с 10-ю пунктами, выбрав любой пункт из меню, можно просмотреть интересующие результаты вычислений.
2.4. Входные данные
Ввод данных – это передача информации от внешних устройств в оперативную память. Вводятся, как правило, исходные данные решаемой задачи.
В моём курсовом проекте входными данными являются числа от 0 до 9, которые вводятся при выборе пункта меню с цифровой клавиатуры. В разделе переменных они у меня записаны типом Byte. Byte– это целочисленный тип данных я его взял потому, что числа от 0 до 9 являются целыми числами. Длина Byte – 1 байт, а диапазон значений от 0 до 255.
2.5. Выходные данные.
Вывод данных – это обратный процесс вводу данных, когда данные передаются из оперативной памяти на внешние носители (принтер, дисплей, магнитные устройства и т.д.). Результаты решения всякой задачи должны быть выведены на один из этих носителей. Как и в моем курсовом проекте все результаты вычислений выводятся на дисплей монитора.
Основным устройством вывода у персонального компьютера является дисплей (экран монитора).
Все результаты вычислений я выводил на дисплей с помощью оператора Write(<Список вывода>). Здесь элементами списка вывода могут быть выражения различных типов (в частности, константы и переменные). У меня элементами списка вывода являются переменные.
Второй вариант процедуры вывода на экран: Writeln(<список вывода>), слово – Write line – означает писать строку. Его действие отличается от оператора Write тем, что после вывода последнего в списке значения происходит перевод курсора к началу следующей строки. Оператор Writeln, записанный без параметров, вызывает перевод строки.
Форматы вывода. В списке вывода могут присутствовать указатели форматов вывода (форматы). Формат определяет представление выводимого значения на экране. Он отделяется от соответствующего ему элемента двоеточием. Если указатель формата отсутствует, то машина выводит значение по определенному правилу, предусмотренному по умолчанию.
2.6. Пример
Для тестирования программы нужно запустить программу нажатием Ctrl+F9 и дождаться появления меню, затем нужно ввести с клавиатуры цифру 1 и сравнить результат выведенной матрицы с матрицей приведённой в таблице №1(выделенное заливкой), они должны совпасть.
3. Проектирование и алгоритмизация.
Метод решения задачи – метод Крамера(по предложенному преподавателем). Метод Крамера имеет весьма простую схему. Пусть detA – определитель матрицы А, а detAi– определитель матрицы Ai, полученной в матрице А столбца с номером i столбцов свободных членов. Тогда метод Крамера сводится к вычислению detA, detAi, i=1,2,…,n, после чего значения неизвестных определяются элементарными соотношениями
Xi=detAi/detA, i=1,2,…n
Определители в этой формуле вычисляются с помощью усеченного метода Гаусса. Действительно, прямой ход метода Гаусса приводитк верхней треугольной матрице, определитель которой равен произведению диагональных элементов матрицы. В прямом ходе метода Гаусса на каждом очередном шаге соответствующая строка делится на диагональный элемент. В результате матрица, полученная после прямого хода, имеет на главной диагонали единицы. Поэтому при вычислении определителя методом Гаусса на каждом шаге прямого хода следует вначале запомнить очередной диагональный элемент, а затем производить деление на него элементов строки.
Методом Крамера – это наиболее легкий метод решения систем линейных алгебраических уравнений, является наиболее точным по сравнению с другими методами решения. Достаточно прост и нагляден, обеспечивает приемлемое быстродействие для систем невысокого порядка. Сохраняет преимущества и недостатки методов вычисления определителей. Как вычислительный метод в научных и технических задачах применяется редко.
Блок-схема работы программы :
SHAPE * MERGEFORMAT
|
Начало |
|
Формирование матрицы А |
|
Формирование матрицы R |
|
Нахождение обратной матрицы R1 |
|
Транспонирование матрицы А |
|
Вычисление матрицы AR1At |
|
Решение системы уравнений методом Крамера |
|
Нахождение вектора |
|
Конец |

3.1 Формирование матрицы А:
SHAPE * MERGEFORMAT
|
Начало |
|
A[1,1] := -1; A[1,2] := 0; И т.д. |
|
Конец |

3.2 Формирование матрицы R:
SHAPE * MERGEFORMAT
|
Начало |
|
for i := 1 to 7 do forj := 1 to 7 do |
|
If i = j then |
|
R[i,j] := c[i] |
|
R[i,j] := 0 |
|
да |
|
нет |
|
Конец |

3.3 Формирование обратной матрицы R1:
SHAPE * MERGEFORMAT
|
Начало |
|
For I := 1 to 7 do For j := 1 to 7 do |
|
If I = j then |
|
R1[i , j]:= 1/r[I,j]; |
|
R1[I,j] := 0 |
|
Конец |

3.4 Транспонирование матрицы А:
SHAPE * MERGEFORMAT
|
Начало |
|
For I := 1 to 4 do For j := 1 to 7 do |
|
At [j, i] := A [i, j] |
|
Конец |

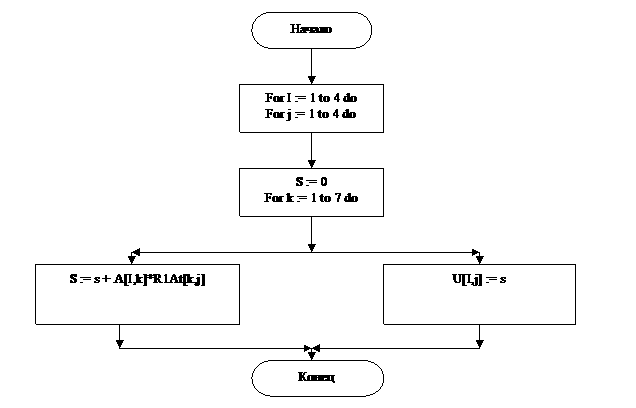
3.5 Вычисление матрицы AR1At :
SHAPE * MERGEFORMAT
|
Начало |
|
For I := 1 to 4 do For j := 1 to 4 do |
|
S := 0 For k := 1 to 7 do |
|
S := s + A[I,k]*R1At[k,j] |
|
U[I,j] := s |
|
Конец |
3.6 Решение системы уравнений методом Крамера :
3.6.1 Описание процедуры замены:
SHAPE * MERGEFORMAT
|
Начало |
|
For I := 1 to 4 do U[I,n] := Q[i] |
|
Конец |

3.6.2 Описание процедуры Opr:
SHAPE * MERGEFORMAT
|
Начало |
|
Dv := u[1,1]*u[2,2]*u[3,3]*u[4,4] + u[1,2]*u[2,3]*u[3,4]*u[4,1] + u[1,3]*u[2,4]*u[3,1]*u[4,2] - u[1,4]*u[2,3]*u[3,2]*u[4,1] - u[1,1]*u[2,4]*u[3,3]*u[4,1] - u[1,2]*u[2,1]*u[3,4]*u[4,3]; |
|
Конец |

3.6.3 Вычисление Х-ов:
SHAPE * MERGEFORMAT
|
Начало |
|
u1 := u; opr; d := dv; n := 1; zamena; |
|
opr; d1 := dv; u := u1; n := 2; zamena; |
|
opr; d3 := dv; u := u1; n := 4; zamena; |
|
opr; d4 := dv; x1 := d1/d; x2 := d2/d; x3 := d3/d; x4 := d4/d; x[1] := x1;x[2] := x2; x[3] := x3;x[4] := x4; |
|
opr; d2 := dv; u:= u1; n := 3; zamena; |
|
Конец |

3.7 Нахождение вектора Р:
SHAPE * MERGEFORMAT
|
Начало |
|
For I := 1 to 7 do S := 0 |
|
For k := 1 to 4 do s := s + r1at[i,k] * x[k]; p[i] := -s |
|
Конец |

4. Кодирование алгоритма.
В моём курсовом проекте я использовал 3 одномерных массива:
X : array [1..4] ofreal;
P: array [1..7] of real;
pr : array [1..4] of real;
Одномерный массив Х вещественного типа мне потребовался для формирования столбца из полученных корней уравнения, решенного методом Крамера.
Массив Р, вещественного типа, я использовал для формирования столбца значений вектора потоков Р.
Массив Pr , вещественного типа, я применил для формирования столбца проверочных данных.
Так же было использовано 6 двумерных массивов:
At : array [1..7,1..4] of shortint;
R : array [1..7,1..7] of shortint;
R1 : array [1..7,1..7] of real;
R1At : array [1..7,1..4] of real;
A : array [1..4,1..7] of shortint;
U,U1 : array [1..4,1..4] of real;
Массив Atиспользуется для формирования транспонированной матрицы А размерностью 7 строк и 4 столбца, элементы которой типа Shortint(т.к. все элементы матрицы являются целыми числами, а в Shortint входят все числа от -128 до +128 ).
Массив R используется для формирования диагональной матрицы размером 7 строк на 7 столбцов все элементы этой матрицы, как и элементы матрицы At Shortintтипа.
Массив R1 – матрица размером 7 строк на 7 столбцов обратная матрице R типа real (вещественный тип данных) т.к. при формировании обратной матрицы нужно применить деление, а при делении частное получается почти всегда вещественного типа.
Массив R1At – матрица размером 7 строк на 4 столбца, полученная в результате умножения матрицы R1 на матрицу At, элементы этой матрицы, как и элементы массива R1 типа real.
Массив A – матрица элементов таб.№1(выделено заливкой) размером 4 строки на 7 столбцов тип Shortint.
Массивы U и U1– это матрица размером 4 строки на 4 столбца полученная в результате умножения:
A

тип элементов матрицы real.
Переменную S я использовал в процедурах умножения матриц, в качестве счётчика тип этой переменной вещественного типа real.
Переменные х1,х2,х3,х4 использованы в решении уравнения методом Крамера в качестве корней уравнения. Тип этих переменных так же вещественный.
d,dv,d1,d2,d3,d4 – переменные вещественного типа d – требуется для создания копии главного определителя dv. d1 - d4 – определители требующиеся для нахождения корней уравнения.
Переменные i,jнужны для счётчиков в операциях с матрицами i – это строки, j – это столбцы тип этих переменных integer (целый тип данных).
Переменная kиспользована при умножении матриц в качестве дополнительного счётчика тип integer.
n – переменная, использованная в процедуре замены для определения номера вырезаемого столбца тип переменной – integer.
nr – переменная типа byte (длина 1 байт, диапазон значений от 0 до 255) потребовалась в процедуре номеров пунктов меню.
5. Руководство ползователя.
5.1 Пуск
Запуск из среды Turbo Pascal производится нажатием клавиш Ctrl+F9, а из NortonCommander нажатием клавиши Enter на файле Inform.exe.
5.2 Ввод данных
Ввод данных производится только с цифровой клавиатуры. Цифры от 0 до 9.
5.3 Просмотр результатов.
После ввода цифры(нужного пункта в меню) выводится требуемый результат и после просмотра результата нужно нажать Enter. Затем вновь появится меню на экране.
5.4 Выход из программы
Выход из программы в среде Turbo Pascal и после запуска Inform.exeфайла производится 0-ым пунктом меню.
Листинг программы.
uses crt;
var
X : array [1..4] of real;
P : array [1..7] of real;
At : array [1..7,1..4] of shortint;
R : array [1..7,1..7] of shortint;
R1 : array [1..7,1..7] of real;
R1At : array [1..7,1..4] of real;
A : array [1..4,1..7] of shortint;
U,U1 : array [1..4,1..4] of real;
pr,pro : array [1..4] of real;
s,x1,x2,x3,x4,d,d1,d2,d3,d4,dv : real;
i,j,k,n : integer;nr : byte;
const
Q : array [1..4] of integer = (70,100,-160,-80);
C : array [1..7] of byte = (4,5,7,6,5,8,5);
Procedure Titul; begin ClrScr; Window(1,1,80,25);
TextBackGround(blue);
TextColor(10);
ClrScr;
GoToXY(20,2); writeln('Кавминводскийинститутсервиса');
GoToXY(20,5); writeln('Курсовая работа по информатике');
GoToXY(10,8); writeln('студента 2-го курса очного отделения группы ИС-01');
GoToXY(18,11); writeln('Ханина Константина Александровича');
GoToXY(19,14); writeln('Тема работы " Транспортная задача "');
GoToXY(19,17); writeln('Руководитель ст. преп. МакаровБ.С.'); for i:=1 to 20 do Delay(30000)
end;
Procedure Vivod_a; begin
GoToXY(2,2);write('Матрица A');writeln;writeln; for i := 1 to 4 do begin
for j := 1 to 7 do begin
write(a[i,j]:5,' ');
end;writeln;
end
end;
Procedure Vivod_R; begin
GoToXY(2,2);write('Матрица R');writeln;writeln; for i := 1 to 7 do begin
for j := 1 to 7 do begin
write(R[i,j]:3,' ');
end;writeln;
end
end;
Procedure Vivod_R1; begin
GoToXY(2,2);write('Матрица R1');writeln;writeln; for i := 1 to 7 do begin
for j := 1 to 7 do begin
write(R1[i,j]:3:1,' ');
end;writeln;
end
end;
Procedure Vivod_At; begin
GoToXY(2,2);write('Матрица At');writeln;writeln; for i := 1 to 7 do begin
for j := 1 to 4 do begin
write(At[i,j]:5,' ');
end;writeln;
end
end;
Procedure Vivod_AR1At; begin u := u1;
GoToXY(2,2);write('Матрица U');writeln;writeln; for i := 1 to 4 do begin
for j := 1 to 4 do begin
write(U[i,j]:5:1,' ');
end;writeln;
end
end;
Procedure Vivod_Q; begin
GoToXY(2,2);write('Столбецсвободныхчленов Q');writeln;writeln; for i := 1 to 4 do
writeln(Q[i]:7);
end;
Procedure Vivod_U; begin
GoToXY(2,2);write('Столбецвектора U');writeln;writeln; for i := 1 to 4 do
writeln(x[i]:7:1);
end;
Procedure Vivod_P; begin
GoToXY(2,2);write('Столбецвектора P');writeln;writeln; for i := 1 to 7 do
writeln(P[i]:7:1);
end;
Procedure Proverka; begin
for i := 1 to 4 do begin s := 0;
for j := 1 to 7 do
s := s + a[i,j] * p[j];
pr[i] := s;
end;
for i := 1 to 4 do
writeln('pr = ',pr[i]:4:0)
end;
Procedure Screen; begin
clrscr;
GotoXY(5,7);write('1. Сформироватьматрицу A'); GoToXY(5,9);write('2. Сформироватьматрицу R'); GoToXY(5,11);write('3. Найтиобратнуюматрицу R1'); GoToXY(5,13);write('4. Транспонироватьматрицу A'); GoToXY(5,15);write('5. Вычислитьматрицу A*R1*At'); GoToXY(5,17);write('6. Сформировать стлбец свободных членов Q'); GoToXY(5,19);write('7. Pешить систему уравнений т.е. найти вектор U'); GoToXY(5,21);write('8. Найти вектор P'); GoToXY(5,23);write('9. Проверка !!!'); GoToXY(5,25);write('0. Выход ???');
GoToXY(20,30);write('В В Е Д И Т Е Н О М Е P П У Н К Т А - '); readln(nr);clrscr;
case nr of
1: vivod_a;
2: vivod_R;
3: vivod_R1;
4: vivod_At;
5: vivod_AR1At;
6: vivod_Q;
7: vivod_U;
8: vivod_P;
9: Proverka;
0: halt;
else
writeln('Выввелинеправильнопункт');
end;
end;
Procedure opr; begin
dv :=u[1,1]*u[2,2]*u[3,3]*u[4,4] + u[1,2]*u[2,3]*u[3,4]*u[4,1] +
u[1,3]*u[2,4]*u[3,1]*u[4,2] - u[1,4]*u[2,3]*u[3,2]*u[4,1] -
u[1,1]*u[2,4]*u[3,3]*u[4,2] - u[1,2]*u[2,1]*u[3,4]*u[4,3];
end;
Procedure Zamena; begin
fori := 1 to 4 do
u[i,n] := Q[i]
end;
Procedure formA; begin
(*------------------Формирование матрицы А------------------------*)
a[1,1]:=-1;a[1,2]:=0;a[1,3]:=0;a[1,4]:=0;a[1,5]:=1;a[1,6]:=0;a[1,7]:=0;
a[2,1]:=0;a[2,2]:=-1;a[2,3]:=0;a[2,4]:=0;a[2,5]:=-1;a[2,6]:=-1;a[2,7]:=0;
a[3,1]:=0;a[3,2]:=0;a[3,3]:=1;a[3,4]:=0;a[3,5]:=0;a[3,6]:=1;a[3,7]:=1;
a[4,1]:=0;a[4,2]:=0;a[4,3]:=0;a[4,4]:=1;a[4,5]:=0;a[4,6]:=0;a[4,7]:=-1; end;
Procedure formR; begin
(*--------------------Формиррованиематрицы R-----------------------*)
for i := 1 to 7 do
for j := 1 to 7 do
if i=j then r[i,j] := c[i] else r[i,j]:=0;
end;
Procedure formR1; begin
(*---------------------Формированиематрицы R1-----------------------*)
for i := 1 to 7 do
for j := 1 to 7 do
if i=j then
r1[i,j] := 1/r[i,j] else
r1[i,j] := 0;
end;
Procedure transA; begin
(*--------------------Транспонирование матрицы А---------------------*)
for i := 1 to 4 do begin
for j := 1 to 7 do begin
At[j,i] := A[i,j]; end;end;
end;
Procedure umnosh; begin
(*------------------------Умножение R1*At----------------------------*)
for i := 1 to 7 do
for j := 1 to 4 do begin
s := 0;
for k := 1 to 7 do
s := s + R1[i,k] * At[k,j];
R1At[i,j] := S end;
end;
Procedure vychisl; begin
(*---------------------Вычислениематрицы A*R1At--------------------*)
for i := 1 to 4 do
for j := 1 to 4 do
begin
s := 0;
for k := 1 to 7 do
s := s + A[i,k] * R1At[k,j];
U[i,j] := s end;
end;
(*---------------------Управляющая программа------------------------*)
Begin
TiTul;
FormA;
FormR;
FormR1;
TransA;
Umnosh;
Vychisl;
u1 := u;
opr;
d := dv;
n := 1;
zamena;
opr;
d1 := dv;
u:= u1;
n := 2;
zamena;
opr;
d2 := dv;
u:= u1;
n:= 3;
zamena;
opr;
d3 := dv;
u:= u1;
n:= 4;
zamena;
opr;
d4 := dv;
x1 := d1/d; x2 := d2/d; x3 := d3/d; x4 := d4/d;
x[1] := x1;x[2] := x2;x[3] := x3;x[4] := x4;
for i := 1 to 7 do
begin s := 0;
for k := 1 to 4 do
s := s - r1at[i,k] * x[k];
p[i] := s
end;writeln;
for i := 1 to 10 do begin
Screen;readln; end;
End.