Проектирование и исследование механизмов двигателя внутреннего сгорания
| Загрузить архив: | |
| Файл: ref-16009.zip (375kb [zip], Скачиваний: 60) скачать |
Министерство образования РФ
Вологодский государственный
технический университет
Факультет: ФПМ
Кафедра: ТПММ
Дисциплина: ТММ
Расчётно-пояснительная записка
к курсовому проекту
Тема проекта: проектирование и исследование
механизмов двигателя внутреннего сгорания
КП1502.19.01.00.
Руководитель: доц. Рябинина Л.Н.
Разработал: студент гр. МАХ – 31
Кузнецов С.А.
г. Вологда,
2000 г.
Содержание
TOC o "1-2" h z Введение- PAGEREF _Toc503300925 h 3
1. Исходные данные- PAGEREF _Toc503300926 h 4
2. Проектирование рычажного механизма. PAGEREF _Toc503300927 h 5
2.1 Структурный анализ механизма. PAGEREF _Toc503300928 h 5
2.2 Синтез рычажного механизма- PAGEREF _Toc503300929 h 6
2.4 Исследование механизма методом кинематических диаграмм- PAGEREF _Toc503300931 h 8
2.5 Определение приведённых моментов сил. PAGEREF _Toc503300932 h 9
2.7 Силовой анализ рычажного механизма. PAGEREF _Toc503300933 h 13
2.8 Кинетостатический расчёт механизма. PAGEREF _Toc503300934 h 14
2.9 Проверка уравновешивающего момента методом рычага Жуковского. PAGEREF _Toc503300935 h 16
3. Проектирование зубчатой передачи. PAGEREF _Toc503300936 h 17
3.1 Синтез зубчатой передачи. PAGEREF _Toc503300937 h 17
3.2Построение геометрической картины эвольвентного зубчатого зацепления. PAGEREF _Toc503300938 h 18
3.3 Синтез планетарного редуктора. PAGEREF _Toc503300939 h 19
4 Синтез кулачкового механизма. PAGEREF _Toc503300940 h 20
4.1 Задача синтеза кулачкового механизма. PAGEREF _Toc503300941 h 21
4.2 Построение диаграммы аналогов ускорений. PAGEREF _Toc503300942 h 21
4.4 Определение минимального радиуса кулачка. PAGEREF _Toc503300944 h 21
4.5 Профилирование кулачка. PAGEREF _Toc503300945 h 21
Списокиспользованной литературы: PAGEREF _Toc503300946 h 22
Введение
Курсовое проектирование несёт собой задачу по развитию навыков анализа и основам конструирования механизмов.
Из множества решений конструктор выбирает наиболее целесообразное и выгодное.
Курсовое проектирование обеспечивает конструкторскую подготовку инженера, которая должна отличаться рациональностью и эффективностью.
1. Исходные данные:
1) 1=2000 об/мин.
2) ср=9,0 м/с.
3) l=3,6
4)
5) ш=2,8 кг.
6) п=3,0 кг.
7) max=5´106 Н/м2.
8) d=1/30.
9) j1=330°.
10)
11)jp=120°.
12)
13)
14)1=14; z2=24.
15)6=3,8.
16)
Примечание:
1. AB=lCD=l.
2.lAS2=lAS4=0,35´l.
3.
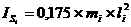
2. Проектирование рычажного механизма.
2.1 Структурный анализ механизма.
Данный механизм состоит из пяти подвижных звеньев:
1 – кривошип;
2,4 – шатуны;
3,5 – ползуны.
В механизме семь кинематических пар:
I: стойка 6 – кривошип 1 – вращательное движение
II: кривошип 1 – шатун 2 – вращательное движение
III: шатун 2 – ползун 3 – вращательное движение
IV: ползун 3 – стойка 6 – вращательное движение
V: кривошип 1 – шатун 4 – вращательное движение
VI: шатун 4 – ползун 5 – вращательное движение
VII: ползун 5 – стойка 6 – вращательное движение
Все кинематические пары пятого класса (p5).
По формуле Чебышева определим степень подвижности механизма (W):

где n – число подвижных звеньев;
p5 – число кинематических пар пятого класса;
p4 – число кинематических пар четвёртого класса;

что говорит о том, что в данном механизме одно ведущее звено. Согласно классификации Артоболевского данный механизм:
1.
|
Условное обозначение |
n |
p5 |
p4 |
Характеристики |
||
|
класс |
порядок |
вид |
||||
|
2 |
3 |
0 |
2 |
2 |
2 |
|
|
2 |
3 |
0 |
2 |
2 |
2 |
2. -го класса.
— -го класса
Формула строения механизма

 1 (1)
1 (1)
2 (4,5)
2.2 Синтез рычажного механизма
В задачу синтеза входит определение геометрических размеров звеньев.
Дано: число
оборотов кривошипа n1=2000 об/мин, тогда период вращения коленвала 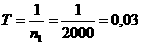 с. Средняя скорость
движения ползуна vср=9,0 м/с если
с. Средняя скорость
движения ползуна vср=9,0 м/с если 


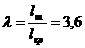


Найдём положения центров масс на шатунах по заданному соотношению:
lAS2=lAS4=0,35´l,
где l – длина шатуна. Тогда lAS2=lAS4=0,35´0,243»0,085 м.
2.3 Определение скоростей точек и угловых скоростей звеньев методом планов.
Скорость точек можно определить методом планов скоростей. Кинематическое исследование этим методом производится в следующей последовательности:
1.
2.
Механизм вычерчивается в определённом масштабе, который выражается масштабным коэффициентом:


где lО1А – действительное значение длины звена; ОА – отрезок, изображающий длину на чертеже.
Для построения положений звеньев механизма и траекторий, по которым перемещаются точки, применяется метод геометрических мест (засечек). Планы механизмов строятся для последовательно располагающихся равноотстоящих положений ведущего звена. Кинематическое исследование проводится для одного цикла движения. Соединяя последовательно положения одной и той же точки звена, получим траекторию движения точки.
Результат графического решения уравнения, связывающего две скорости двух точек звена, называется планом скоростей звена. Векторы относительных скоростей не проходят через полюс плана скоростей, если звено не совершает вращательного движения вокруг точки, принадлежащей этому звену. Векторы абсолютных скоростей начинаются в полюсе плана скоростей.
Рассмотрим построение плана скоростей для одного положения механизма. Определим скорость точки А ведущего звена.

где 
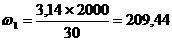 -1,
-1,  ^ О1А.
^ О1А.
Зададимся
масштабным коэффициентом: 
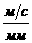
Составимвекторные уравнения для присоединённых групп Ассура с целью определения скоростей точек В и С.
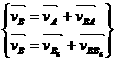 ВА ^ АВ; vВВ6 II х-х; vВ6=0.
ВА ^ АВ; vВВ6 II х-х; vВ6=0.
 DА ^ АD; vDD6 II х-х; vD6=0.
DА ^ АD; vDD6 II х-х; vD6=0.
Выбрав полюс pv и, задавшись масштабным коэффициентом, строим планы скоростей для всех положений механизма. По правилу подобия: фигура, образованная на плане скоростей векторами относительных скоростей, подобна соответствующей фигуре на кинематической схеме механизма и повернута относительно её на 90° по направлению угловой скорости. Отсюда следует, что точки S2 и S4 на плане скоростей определятся из пропорций:
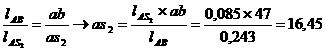
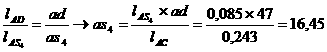
Скорости точек S2 и S4 определяются векторами, соединяющими эти точки с полюсом.
Угловые скорости звеньев находим:
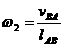

Числовые значения скоростей для положения I определяются следующим образом:


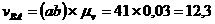
 м/с
м/с
 м/с
м/с
 м/с, тогда
м/с, тогда
 -1,
-1,
Результаты измерений и вычислений занесём в таблицу 1.
Таблица SEQ Таблица * ARABIC 1
|
№ п/п |
vа, м/с |
vс, м/с |
vb, м/с |
vd, м/с |
vаb, м/с |
vcd, м/с |
vS2, м/с |
vS4, м/с |
w2, с-1 |
w4, с-1 |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
0 |
14,137 |
14,137 |
0,00 |
0,00 |
14,10 |
14,10 |
9,30 |
9,30 |
58,02 |
58,02 |
|
1 |
8,70 |
5,40 |
12,30 |
12,30 |
11,10 |
10,20 |
50,62 |
50,62 |
||
|
2 |
14,10 |
10,50 |
7,20 |
7,20 |
13,80 |
12,60 |
29,63 |
29,63 |
продолжение таблицы 1
|
1 |
2 |
3 |
4 |
5 |
6 |
8 |
9 |
10 |
11 |
|
|
3 |
14,137 |
14,137 |
14,10 |
14,10 |
0,00 |
0,00 |
14,10 |
14,10 |
0,00 |
0,00 |
|
4 |
10,50 |
13,95 |
7,50 |
7,50 |
12,60 |
13,50 |
30,86 |
30,86 |
||
|
5 |
5,10 |
8,40 |
12,60 |
12,60 |
10,20 |
11,10 |
51,85 |
51,85 |
||
|
6 |
0,00 |
0,00 |
14,10 |
14,10 |
9,30 |
9,30 |
58,02 |
58,02 |
||
|
7 |
5,10 |
8,70 |
12,30 |
12,30 |
10,50 |
11,10 |
50,62 |
50,62 |
||
|
8 |
10,20 |
14,10 |
7,20 |
7,20 |
12,60 |
13,80 |
29,63 |
29,63 |
||
|
9 |
14,10 |
14,10 |
0,00 |
0,00 |
14,10 |
14,10 |
0,00 |
0,00 |
||
|
10 |
13,95 |
10,50 |
7,20 |
7,20 |
13,50 |
12,60 |
29,63 |
29,63 |
||
|
11 |
8,70 |
5,40 |
12,60 |
12,60 |
11,10 |
10,20 |
51,85 |
51,85 |
||
|
12 |
0,00 |
0,00 |
14,10 |
14,10 |
9,30 |
9,30 |
58,02 |
58,02 |
||
|
13 |
8,70 |
5,40 |
12,30 |
12,30 |
11,10 |
10,20 |
50,62 |
50,62 |
||
|
14 |
14,10 |
10,50 |
7,20 |
7,20 |
13,80 |
12,60 |
29,63 |
29,63 |
||
|
15 |
14,10 |
14,10 |
0,00 |
0,00 |
14,10 |
14,10 |
0,00 |
0,00 |
||
|
16 |
10,50 |
13,95 |
7,50 |
7,50 |
12,60 |
13,50 |
30,86 |
30,86 |
||
|
17 |
5,10 |
8,40 |
12,60 |
12,60 |
10,20 |
11,10 |
51,85 |
51,85 |
||
|
18 |
0,00 |
0,00 |
14,10 |
14,10 |
9,30 |
9,30 |
58,02 |
58,02 |
||
|
19 |
5,10 |
8,70 |
12,30 |
12,30 |
10,50 |
11,10 |
50,62 |
50,62 |
||
|
20 |
10,20 |
14,10 |
7,20 |
7,20 |
12,60 |
13,80 |
29,63 |
29,63 |
||
|
21 |
14,10 |
14,10 |
0,00 |
0,00 |
14,10 |
14,10 |
0,00 |
0,00 |
||
|
22 |
13,95 |
10,50 |
7,20 |
7,20 |
13,50 |
12,60 |
29,63 |
29,63 |
||
|
23 |
8,70 |
5,40 |
12,60 |
12,60 |
11,10 |
10,20 |
51,85 |
51,85 |
||
|
24 |
0,00 |
0,00 |
14,10 |
14,10 |
9,30 |
9,30 |
58,02 |
58,02 |
2.4 Исследование механизма методом кинематических диаграмм
Исследование механизмов методом диаграмм производится с целями:
1.
2.
В курсовом проекте выполним кинематическое исследование методом диаграмм для точек D и С.
Для построения диаграммы перемещений отложим для каждого положения соответствующее перемещения ползунов D и С в масштабе mS.
Кинематические диаграммы скоростей и ускорений строим методом хорд.




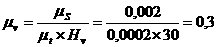
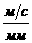


Скорости и ускорения т. В, найденные методом диаграмм, занесём в таблицу 2.
Таблица SEQ Таблица * ARABIC 2
|
Параметр |
Значения в положениях |
|||||||||||
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
|
Скорость т. В, м/с |
0 |
6,9 |
10,2 |
10,2 |
6,3 |
4,8 |
0 |
4,5 |
7,5 |
9,6 |
10,2 |
6,3 |
|
Ускорение т. В, м/с2 |
2600 |
1650 |
600 |
450 |
1000 |
1350 |
1400 |
1325 |
1000 |
450 |
600 |
1650 |
2.5 Определение приведённых моментов сил.
Мпр – расчётный момент пары сил, определяемый из равенства его элементарной работы, равен сумме элементарных работ сил и моментов пар сил, действующих на звенья механизма.
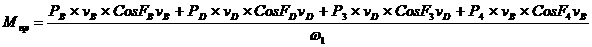
где PB и PD определяются по индикаторной диаграмме.
Пример вычисления Мпр для положения 1:
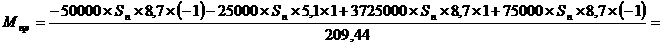 =1698,14 Н´м.
=1698,14 Н´м.
Так как сила действует по направляющей и скорость направлена параллельно направляющей, то косинус угла равен ±1, а угол равен 0° или 180° в зависимости от положения механизма.
Или иначе:


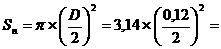 = 3,14´0,0036»0,011
м2– площадь поверхности
поршня.
= 3,14´0,0036»0,011
м2– площадь поверхности
поршня.
Результаты измерений и вычислений занесём в таблицу 3.
Таблица SEQ Таблица * ARABIC 3
|
угол, ° |
PВ, Па |
МВ, Н´м |
Мпр, Н´м |
vB, м/с |
|
1 |
2 |
3 |
4 |
5 |
|
0 |
50000 |
0,00 |
0,00 |
0,00 |
|
30 |
-50000 |
22,85 |
1 698,14 |
8,70 |
|
60 |
-50000 |
37,03 |
1 336,53 |
14,10 |
|
90 |
-50000 |
37,03 |
703,52 |
14,10 |
|
120 |
-50000 |
27,57 |
170,96 |
10,50 |
|
150 |
-50000 |
13,39 |
-249,54 |
5,10 |
|
180 |
-50000 |
0,00 |
0,00 |
0,00 |
|
210 |
-25000 |
-6,70 |
1 698,14 |
5,10 |
|
240 |
12500 |
-6,70 |
1 336,53 |
10,20 |
|
270 |
100000 |
-74,05 |
703,52 |
14,10 |
|
300 |
300000 |
-219,80 |
170,96 |
13,95 |
|
330 |
862500 |
-394,10 |
-249,54 |
8,70 |
|
360 |
1450000 |
0,00 |
0,00 |
0,00 |
|
390 |
3725000 |
1702,07 |
1 698,14 |
8,70 |
|
420 |
1800000 |
1332,98 |
1 336,53 |
14,10 |
|
450 |
1050000 |
777,57 |
703,52 |
14,10 |
|
480 |
725000 |
399,82 |
170,96 |
10,50 |
|
510 |
575000 |
154,02 |
-249,54 |
5,10 |
|
540 |
250000 |
0,00 |
0,00 |
0,00 |
|
570 |
75000 |
-20,09 |
1 698,14 |
5,10 |
продолжение таблицы 3
|
1 |
2 |
3 |
4 |
5 |
|
600 |
50000 |
-26,79 |
1 336,53 |
10,20 |
|
660 |
50000 |
-36,63 |
170,96 |
13,95 |
|
690 |
50000 |
-22,85 |
-249,54 |
8,70 |
|
720 |
50000 |
0,00 |
0,00 |
0,00 |
Строим
диаграмму Мпр=Мпр(j) с масштабным
коэффициентом 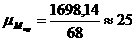


2.5.1 Определение работ сил сопротивления и движущих сил
Интегрируя
диаграмму приведённых моментов сил сопротивления, получим диаграмму работы сил
сопротивления с масштабным коэффициентом: 

Полагая, что приведённый момент сил сопротивления имеет постоянную величину во всех положениях кривошипа, то величину Мдв. определяем на основе законапередачи работы при установившемся режиме действия механизма.
За период установившегося движения работа движущих сил равна работе сил сопротивления. При этом условии диаграмма Ас=Ас(j) работ сил сопротивления будет представлять собой наклонную прямую, соединяющую начало координат с последней точкой графика.
Продифференцировав диаграмму Ас=Ас(j), получим на диаграмме Мпр прямую, которая и является диаграммой моментов сил сопротивления.
2.5.2 Определение суммарной работы.
Вычитая из ординат график Ад=Ад(j) ординаты графика Ас=Ас(j), получим диаграмму приращения кинетической энергии машины с маховиком или диаграмму суммарной работы.

2.5.3 Определение приведённых моментов инерции.
Приведённый моментов инерции – это такой условный момент, обладая которым звено приведения развивает кинетическую энергию, равную сумме кинетических энергий всех звеньев.
 ,
,
где кг´М2, т.о. IS2=
IS4.
кг´М2, т.о. IS2=
IS4.
Пример расчёта:
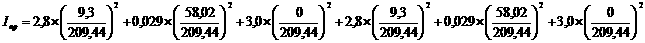 ´м2.
´м2.
Результаты и вычислений занесём в таблицу 4.
Таблица SEQ Таблица * ARABIC 4
|
угол, ° |
Iпр, кг´м2 |
|
1 |
2 |
|
0 |
0,0155 |
|
30 |
0,0251 |
|
60 |
0,0446 |
|
90 |
0,0526 |
|
120 |
0,0439 |
продолжение таблицы 4
|
1 |
2 |
|
150 |
0,0247 |
|
180 |
0,0155 |
|
210 |
0,0252 |
|
240 |
0,0442 |
|
270 |
0,0526 |
|
300 |
0,0438 |
|
330 |
0,0252 |
|
360 |
0,0155 |
|
390 |
0,0251 |
|
420 |
0,0446 |
|
450 |
0,0526 |
|
480 |
0,0439 |
|
510 |
0,0247 |
|
540 |
0,0155 |
|
570 |
0,0252 |
|
600 |
0,0442 |
|
630 |
0,0526 |
|
660 |
0,0438 |
|
690 |
0,0252 |
|
720 |
0,0155 |
2.5.4 Построение диаграммы Т2=Т2(j)
Определим кинетическую энергию по формуле:


Найденные значения записываем в таблицу 5.
Таблица SEQ Таблица * ARABIC 5
|
положение |
Т2 |
|
1 |
2 |
|
0 |
339,81 |
|
1 |
549,73 |
|
2 |
977,93 |
|
3 |
1153,10 |
|
4 |
962,32 |
|
5 |
540,97 |
|
6 |
339,81 |
|
7 |
553,70 |
|
8 |
968,61 |
|
9 |
1153,10 |
|
10 |
960,15 |
|
11 |
553,39 |
|
12 |
339,81 |
|
13 |
549,73 |
|
14 |
977,93 |
|
15 |
1153,10 |
|
16 |
962,32 |
|
17 |
540,97 |
|
18 |
339,81 |
|
19 |
553,70 |
продолжение таблицы 5
|
1 |
2 |
|
20 |
968,61 |
|
21 |
1153,10 |
|
22 |
960,15 |
|
23 |
553,39 |
|
24 |
339,81 |
2.5.5 Построение диаграммы изменения кинетической энергии DТ1=DТ1(j).
Строим диаграмму изменения кинетической энергии путём вычитания из кривой суммарной работы значений Т2, при этом диаграмма суммарной работы и Т2 выполнены в одном масштабе.
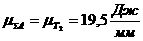
Определяем DТ1наиб. и вычисляем значение Iпр1:
 кг´м2,
кг´м2,
при этом момент инерции маховика 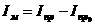 пр0 – момент инерции звена, приведения и
звеньев, связанных со звеном приведения постоянством передаточного отношения.
пр0 – момент инерции звена, приведения и
звеньев, связанных со звеном приведения постоянством передаточного отношения.
2.5.6 Определение размеров маховика.
Момент инерции маховика коленвала должен быть таким, чтобы колебания угловой скорости машины, заданные коэффициентом неравномерности вращения s не выходил за предел колебания угловой скорости wmax и wmin.
Если  пр0=0, то
пр0=0, то  кг´м2.
Масса маховика определяется по формуле:
кг´м2.
Масса маховика определяется по формуле:

где Dср –
средний диаметр маховика принимаем равным 0,4 м, т.о.  кг. Зная массу и
плотность (g=7800
кг/м3), вычислим значения S и b:
кг. Зная массу и
плотность (g=7800
кг/м3), вычислим значения S и b:
1). Находим
объём маховика:  м3.
м3.
2). Определим
толщину S и ширину обода b: 

 Þ S=0,4´0,055=0,022 м.
Þ S=0,4´0,055=0,022 м.
2.5.7 Определение закона движения ведущего звена
При принятых допущениях изменение угловой скорости Dw1 ведущего звена пропорционально изменению кинетической энергии DТ1 звеньев первой группы. В Связи с этим, диаграмма DТ1=f(j1) может являться и диаграммой угловой скорости кривошипа w1, если принять равенство соответствующих ординат.

Т.к. mDТ1уже выбран, то
масштабный коэффициент mw определяется следующим образом: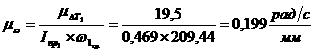
Начало
координат осей на диаграмме w1=f(j1)
определяется ординатой 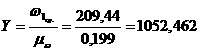
Дифференцируем диаграммуw1=f(j1) и получаем диаграмму аналога углового ускорения кривошипа ej=f(j1). При этом масштабный коэффициент вычисляется по формуле:
 e - полюсное расстояние, Нe=30
мм.
e - полюсное расстояние, Нe=30
мм. 
Для определения углового ускорения кривошипа e1 воспользуемся следующей формулой:
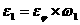
Пример расчёта: ej=[ej]´me=22 мм´0,255 с-1/мм=5,61 с-1, тогда
e1=5,61´209,03=1172,648 рад/с2.
Результаты измерений и вычислений занесём в таблицу 6.
Таблица SEQ Таблица * ARABIC 6
|
положение |
Dw1 |
w1 |
e1 |
ej |
|
0 |
1,8 |
211,20 |
0 |
0,00 |
|
1 |
0,9 |
210,35 |
1180,081 |
5,61 |
|
2 |
-1,1 |
208,37 |
1328,367 |
6,38 |
|
3 |
-1,8 |
207,68 |
0 |
0,00 |
|
4 |
-0,4 |
209,03 |
1172,648 |
5,61 |
|
5 |
1,7 |
211,14 |
1346,011 |
6,38 |
|
6 |
1,8 |
211,20 |
0 |
0,00 |
|
7 |
0,9 |
210,31 |
1179,854 |
5,61 |
|
8 |
-1,0 |
208,47 |
1328,973 |
6,38 |
|
9 |
-1,8 |
207,68 |
0 |
0,00 |
|
10 |
-0,4 |
209,05 |
1172,772 |
5,61 |
|
11 |
1,6 |
211,01 |
1345,203 |
6,38 |
|
12 |
1,8 |
211,20 |
0 |
0,00 |
|
13 |
0,9 |
210,35 |
1180,081 |
5,61 |
|
14 |
-1,1 |
208,37 |
1328,367 |
6,38 |
|
15 |
-1,8 |
207,68 |
0 |
0,00 |
|
16 |
-0,4 |
209,03 |
1172,648 |
5,61 |
|
17 |
1,7 |
211,14 |
1346,011 |
6,38 |
|
18 |
1,8 |
211,20 |
0 |
0,00 |
|
19 |
0,9 |
210,31 |
1179,854 |
5,61 |
|
20 |
-1,0 |
208,47 |
1328,973 |
6,38 |
|
21 |
-1,8 |
207,68 |
0 |
0,00 |
|
22 |
-0,4 |
209,05 |
1172,772 |
5,61 |
|
23 |
1,6 |
211,01 |
1345,203 |
6,38 |
|
24 |
1,8 |
211,20 |
0 |
0,00 |
2.7 Силовой анализ рычажного механизма.
2.7.1 Определение ускорений точек методом планов.
Ускорения точек звеньев и угловые ускорения находим для заданного 4-го положения механизма (j1=330°), для которого нужно провести силовой анализ.
Определяем ускорения точек А и С:


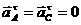 w1=const, то
w1=const, то  2.
2.
Для определения ускорений точек В и D составляем следующие векторные уравнения:
 ^ АВ
^ АВ
 úï
ОY
úï
ОY
 ^ СD
^ СD
 úï
OY, строим план ускорений с масштабным коэффициентом mа= 36 м/с2.
úï
OY, строим план ускорений с масштабным коэффициентом mа= 36 м/с2.
Из произвольно выбранного полюса p, зная направление и величину, откладываем ускорения т. А и С в выбранном масштабе. Из конца этого вектора откладываем нормальные составляющие аВАn и аСDn, параллельные соответственно АВ и CD. Из концов этих векторов проводим линии действия тангенциальных составляющих, перпендикулярных АВ и CD. Из полюса проводим линии действия ускорений т. В и D параллельно линии перемещения ползунов. Получим ускорения точек В и D. Ускорения центров масс шатунов находим по теореме подобия:
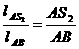

откуда получаем, что 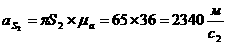



Определение числовых значений:
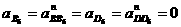
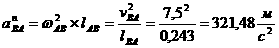







2.7.2 Определение угловых ускорений шатунов.
Угловые ускорения шатунов определяются по формулам:
 D -
D -  .
.
2.8 Кинетостатический расчёт механизма.
Основной задачей силового анализа является определение реакций в кинематических парах механизма, с учётом всех сил, действующих на его звенья и определение уравновешивающей силы или момента, приведённого к ведущему звену.
2.8.1 Определение сил и моментов, действующих на звенья механизма:
Силы, действующие на поршень, определяются с помощью индикаторной диаграммы:
РВ4=-50000 Па, Sп=p´r2=3,14´(0,120 м/2)2=3,14´0,004 м2=0,011 м2, тогда FВ=РВ4´Sп=
=-50000 Па´0,011 м2=-550 Н;
РD4=300000 Па, Sп=p´r2=3,14´(0,120 м/2)2=3,14´0,004 м2=0,011 м2, тогда FD=РВ4´Sп=
=300000 Па´0,011 м2=3300 Н;
Силы инерции:

FИ2=-2,8 кг´2340 м/с2=-6552 Н;
FИ3=-3,0 кг´1800 м/с2=-5400 Н;
FИ4=-2,8 кг´2160 м/с2=-6048 Н;
FИ5=-3,0 кг´1044 м/с2=-3132 Н;
Моменты вычисляются по формуле:

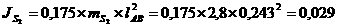
 Н´м,
аналогично
Н´м,
аналогично 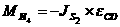

 Н´м.
Н´м.
Силовой расчёт ведут с группы, наиболее удалённой от ведущего звена, механизм рассматриваем в четвёртом положении.
2.8.2 Анализ присоединённых групп Ассура.
Выделяем группы Ассура, состоящие из второго и третьего, четвёртого и пятого звеньев, прикладываем все силы, действующие на звенья, а также все моменты инерции и моменты этих сил. Взамен отброшенных связей прикладываем реакции. Реакцию во вращательной паре раскладываем на нормальную (вдоль звена) и тангенциальную (перпендикулярно звену) составляющие. Выбираем масштабный коэффициент mс.г.=0,0035 м/мм.
2.8.2.1 Группа 3-2.
Условие равновесия системы:
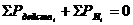


Определение реакций:

 h1
определяем из чертежа, mс.г.=0,0035 м/мм
h1
определяем из чертежа, mс.г.=0,0035 м/мм
[h1]=26 мм, тогда h1=[h1]´ mс.г.=26´0,0035=0,091 м

2.8.2.2 Группа 5-4.
Условие равновесия системы:
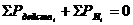


Определение реакций:

 h2]=41
мм, тогда h2=[h2]´
mс.г.=41´0,0035=0,1435
м
h2]=41
мм, тогда h2=[h2]´
mс.г.=41´0,0035=0,1435
м

Строим планы сил с масштабным коэффициентом mс.а.1=100 Н/мм и mс.а.2=70 Н/мм и из него находим:
[R12n]=113 мм - R12n=[R12n]´ mс.а.1=113´100=11300 Н; [R12t]=3726,5/100=37,265 мм
[R63]=11 мм – R63=[R63]´ mс.а.1=11´100=1100 Н; [R14t]=4844,395/70=69,266 мм
[R14n]=38,5 мм - R14n=[R14n]´ mс.а.2=38,5´70=2695 Н;
[R65]=8 мм – R65=[R65]´ mс.а.2=8´70=560 Н;
[R12]=109 мм – R12=[R12]´ mс.а.1=109´100=10900 Н;
[R14]=87 мм – R14=[R14]´ mс.а.2=87´70=6090 Н.
2.8.3 Силовой анализ механизма 1-го класса.
Строим
положение кривошипа с масштабным коэффициентом m1=0,001 м/мм и
к точкам А и С прикладываем реакции 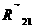 и
и 
 и
и 


На звено 1 также действует момент сил инерции:

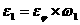 ej=[ej]´me=22 мм´0,255 с-1/мм=5,61 с-1, тогда
ej=[ej]´me=22 мм´0,255 с-1/мм=5,61 с-1, тогда
e1=5,61´209,03=1172,648
рад/с2. кг´м2,
тогда
кг´м2,
тогда
 Н´м.
Н´м.
Также к звену приложен уравновешивающий момент Му. Для определения, которого составим уравнение моментов относительно точки О.

[h41]=6 мм – h41=[h41]´ m1=6´0,001=0,006 м.
[h21]=14 мм – h21=[h21]´ m1=14´0,001=0,014 м.

 ´м.
´м.
2.9 Проверка уравновешивающего момента методом рычага Жуковского.
Суть метода заключается в том, что сумма моментов всех сил, действующихна механизм, включая и силы инерции, перенесённые параллельно себе в одноимённые точки повёрнутого на 90° плана скоростей, относительно полюса Рv равна нулю. План скоростей рассматривается как жёсткий рычаг.
План скоростей для четвёртого положения поворачиваем на 90° по направлению угловой скорости w1, и прикладываем все силы. Моменты инерции приводим к паре сил.
[h1]=12 мм;[h2]=13 мм;[h3]=8 мм;[h4]=33 мм;[hFИ2]=14 мм;[hFИ4]=16 мм;
[ob]=34 мм;[od]=47 мм;[ao]=47 мм;
Составим уравнение моментов относительно полюса:



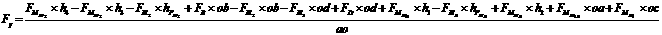
3. Проектирование зубчатой передачи.
3.1 Синтез зубчатой передачи.
3.1.1 Алгоритм расчёта
Параметры инструмента, зависящие от угла наклона зубьев b.




1). Радиусы делительных окружностей:

2). Радиусы основных окружностей:

Расчётные
коэффициенты смещения х1 и х2 для рассчитываемой передачи
должны прежде всего обеспечивать отсутствие подреза (хmin) и
заострения зубьев (хmax), а также гарантировать минимально
допустимую величину коэффициента перекрытия. Следовательно, должно соблюдаться
условие хtmin
3). Минимальное число зубьев на нулевом колесе, которое можно нарезать без подреза:
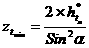
4). Минимальные коэффициенты смещения:

Максимальный
коэффициенты смещения не может быть определён непосредственно, отсутствие заострения
может быть выявлено после подсчёта толщины зуба по окружности вершин и
удовлетворено при условии: 
5). Выбор коэффициента смещения:
Коэффициент смещения х2 выбирается по ГОСТ-18532-83.
6). Угол зацепления передачи:
Решается с помощью подпрограммы RIMT
7). Коэффициент воспринимаемого смещения:

8). Коэффициент уравнительного смещения:
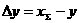
9). Радиусы делительных окружностей:

10). Межосевое расстояние передачи:

11). Радиусы окружностей вершин:

12). Радиусы окружностей вершин:

13). Высота зубьев колёс:

14). Толщина зубьев по дугам делительных окружностей:

15). Углы профиля на окружностях вершин зубьев колёс:
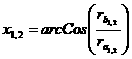
16). Толщина зубьев на окружностях вершин зубьев колёс:
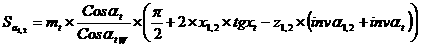
Качественные показатели передачи.
1). Коэффициент перекрытия зубчатой передачи:
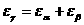


2). Коэффициент скольжения:


3.1.4 Анализ результатов расчёта на ЭВМ.
Для построения картины зубчатого зацепления необходимо выбрать значения параметров зубчатого зацепления, приведенные на стр. 19 в распечатке расчётов на ЭВМ. Для этого нужно определить величину х1 – расчётного коэффициента смещения.
3.2 Построение геометрической картины эвольвентного зубчатого зацепления.
3.2.1 Откладываем межосевое расстояние аW=O1O2 – сумму радиусов начальных окружностей.
3.2.2 Проводим радиусы выступов (ra1, ra2), ножек (rf1, rf2), основных (rb1, rb2) и делительных (r1, r2) окружностей.
3.2.3 Проверяем радиальный зазор с=с*´m, где с*=0,25.
3.2.4 Проводим радиусы основных окружностей и отмечаем на них точки N1 и N2, O1N1 расположится под углом к O1O2 - aWt=25° 04'01", O2N2 - aWt=25° 04'01".
3.2.5 Через точки N1 и N2 проводим общую касательную к окружностям rb1 и rb2. N1N2 – есть теоретическая линия зацепления.
3.2.6 Расстояние N1Р по теоретической линии зацепления N1N2 делим на 4 равные части. Такие же отрезки откладываем за точку N1 и получаем точки 1-6.
3.2.7 Из точки 3 раствором циркуля "3-Р" делаем на rb1 засечку – точка q. Дугу основной окружности rb1 – qN1 делим на 4 равные части и продолжаем деления за точку N1, получаем точки 1,2,3,4,5.
3.2.8 Точки на основной окружности соединяем с центром вращения шестерни.
3.2.9 Перпендикулярно радиусам проводим касательные к основной окружности в каждой точке.
3.2.10 Замеряем расстояние по теоретической линии зацепления: 1Р, 2Р, …, 6Р и из точек 1', 2', …, 6' делаем засечки на соответствующих касательных.
3.2.11 Соединяем полученные точки на касательных, получаем эвольвенту 1-го колеса.
3.2.12 Строим ножку зуба. Дляэтого точку q соединяем с центром вращения 1-го колеса и радиусом rf=0,38´m делаем скругления.
3.2.13 Отложив толщину зуба по дуге делительной окружности S1, строим левый профиль зуба. Разделив толщину зуба пополам, получаем ось симметрии зуба.
3.2.14 Отложив шаги Рt на хорде делительной окружности влево и вправо, получаем оси 2-го и 3-го зубьев и строим три зуба второго колеса.
3.2.15 Определяем длины активной линии зацепления АВ. Расстояния по теоретической линии зацепления N1N2 между точками пересечения окружностей выступов каждого колеса с теоретической линией зацепления – есть практическая линия зацепления.
3.2.16 Определяем дуги зацепления. Через точки теоретической линией зацепления Н1 и Н2 проводимправый профиль зуба первого колеса и левый профиль второго колеса.
3.2.17 Определяем рабочие части боковых профилей зубьев. Радиусами О1Н2 иО2Н1 проводим дуги до пересечения с боковыми профилями зубьев.
3.3 Синтез планетарного редуктора.
3.3.1 Выбор числа зубьев методом обращения движения.
 Þ
Þ
принимаем z4=40,
тогда z6=2,8´40=112>85 – целое число. Число z5
определяем из условия соседства: 
3.3.2 Проверка условия сборки.
Приняв z4=40, z5=36, z6=112, проверяем передачу на условие сборки без натягов (при k=4; p=0):
 – целое число, условие
соблюдается.
– целое число, условие
соблюдается.
3.3.3. Определение размеров планетарного редуктора.

d4=m´z4=8´40=320 мм
d5=m´z5=8´36=288 мм
d6=m´z6=8´112=896 мм
3.3.4 Графическое построение редуктора, планов линейных и угловых скоростей.
Вычерчиваем полученный механизм в масштабе ml=0,0064 м/мм и на вертикальную прямую сносим все характерные точки.
w4=w1=209,44 рад/с., тогда vА=w1´r4=209,44´0,16=33,51 м/с. Строим картину линейных скоростей с масштабным коэффициентом mv=vА/lvА=33,51 (м/с)/44 (мм)=0,7616 м/с/мм. Определяем скорости точек по картине линейных скоростей:
vC=0
vO=0
vB=lvВ´mv=32 (мм)´ 0,7616 (м/с/мм)= 24,37 м/с.
Для построения
плана угловых скоростей откладываем отрезок ОО и из нижнего его конца проводим
лучи, параллельные картинам скоростей звеньев. Угловые скорости изображены с
масштабным коэффициентом 

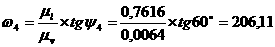 w4= lw4´mw=75´2,7294=204,71
рад/с;
w4= lw4´mw=75´2,7294=204,71
рад/с;
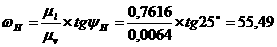 рад/с, по построению -
w4=
lw4´mw=20´2,7294=54,59
рад/с;
рад/с, по построению -
w4=
lw4´mw=20´2,7294=54,59
рад/с;
 рад/с, по построению -
w4=
lw4´mw=75´2,7294=119
рад/с;
рад/с, по построению -
w4=
lw4´mw=75´2,7294=119
рад/с;
4 Синтез кулачкового механизма.
4.1 Задача синтеза кулачкового механизма.
Задача синтеза кулачкового механизма состоит в том, чтобы построить профиль кулачковой шайбы, удовлетворяющей заданным требованиям.
1). Закон движения толкателя.
2). Угловая скорость кулачка.
3). Рабочий угол профиля jр=120°.
4). Перемещение толкателя h=12 мм.
5). Отношение
максимального ускорения толкателя к минимальному
4.2 Построение диаграммы аналогов ускорений.
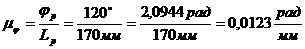
4.3 Построение диаграммы аналогов скоростей и перемещения толкателя методом графического интегрирования.
Масштабные коэффициенты:
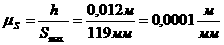

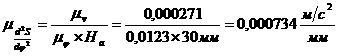
4.4 Определение минимального радиуса кулачка.
При
определении минимального радиуса кулачка с поступательно движущимся толкателем
строится диаграмма зависимости перемещения от аналога скоростей S=f(

 aдоп.=45° к
горизонтальной оси. На пересечении с осью S получаем точку О – расстояние от
неё до горизонтальной оси и есть минимальный радиус кулачка, он равен rmin=ОА´m=105´0,0004=
=0,042 м, принимаем rк=0,045 м.
aдоп.=45° к
горизонтальной оси. На пересечении с осью S получаем точку О – расстояние от
неё до горизонтальной оси и есть минимальный радиус кулачка, он равен rmin=ОА´m=105´0,0004=
=0,042 м, принимаем rк=0,045 м.
4.5 Профилирование кулачка.
При графическом методе построения кривой профиля кулачка используют метод обращения движения: кулачок на чертеже считают неподвижным, а стойку – вращающейся с угловой скоростью (-w11).
Строим положение механизма с масштабным коэффициентом ml=0,0005 м/мм.
Проводим окружность радиусом rк, угол рабочего профиля, который делим на 17 частей – углы, величина которых определяется по диаграмме аналогов ускорений. Продолжаем прямые, делящие угол рабочего профиля, и откладываем на них от радиуса величину хода толкателя. Соединяя точки линией, получаем профиль кулачка.
Список использованной литературы:
1). Артоболевский И.И. "Теория механизмов и машин" М., "Наука", 1975 г.
2). Дерягин Р.В. "Задания на курсовой проект": Ч.2. – Вологда: ВоПИ, 1983. – 42 с.
3). Дерягин Р.В., Рябинина Л.Н. "Кинематический и силовой анализ плоского рычажного механизма": методические указания к курсовой работе. – Вологда: ВоГТУ, 1999. – 36 с.
4). Попов С.А. "Курсовое проектирование по теория механизмов и механике машин": Учебное пособие для машиностроит. спец. вузов/ Под ред. К.В. Фролова. – М.: Высш. шк., 1986. – 295 с.: ил.
5). "Теория механизмов и машин": Учеб. для втузов/ К.В. Фролов, С.А. Попов, А.К. Мусатов и др.; Под ред. К.В. Фролова. – М.: Высш. шк., 1987. – 496 с.: ил.