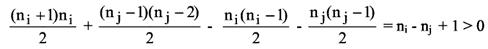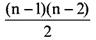Теория графов. Задача коммивояжера

Сдавался/использовалсяИюнь/2004г.
Примечаниеот автора: Нужен титульный лист
Загрузить архив:
Файл: ref-18933.zip (188kb [zip], Скачиваний: 242) скачать

    Содержание

Введение                                                                 

        

I. Основные понятия                                               

1.Эйлеровы графы.                                                             

2. Кротчайшие пути.                                                         

3. Деревья.                                                                                        

II.Задача коммивояжера.                                               

1.Общие описание.                                                                  

2.Методы решения ЗК.                                                      

   а. Жадный алгоритм.                                                       

   б. Деревянный алгоритм.                                                 

   в. Метод ветвей и границ.                                               

III. Выводы.                                                                          

Литература.

                                             Введение.

ТЕОРИЯ ГРАФОВ- это область дискретной матема­тики, особенностью которой является геометрический подход к изучению объектов. Теория графов находится сейчас в самом расцвете. Обычно её относят к топологии (потому что во многих случаях рассматриваются лишь топологические свойства графов), однако она пересекается со многими разделами теории множеств, комбинаторной математики, алгебры, геометрии, теории матриц, теории игр, математической логики и многих других математических дисциплин. Основной объект теории графов-граф и его обобщения.

Первые задачи теории графов были связаны с решением математических развлекательных задач и головоломок (задача о Кенигсбергских мостах, задача о расстановке ферзей на шахматной доске, задачи о перевозках, задача о кругосветном путешествии и другие). Одним из первых результатов в теории графов явился критерий существования обхода всех ребер графа без повторе­ний, полученный Л. Эйлером при реше­нии задачи о Кенигсбергских мостах. Вот пересказ отрывка из письма Эйлера от 13 марта 1736 году: ” Мне была предложена задача об острове, расположенном в городе Кенигсберге и окруженном рекой, через которую перекинуто 7 мостов. Спрашивается, может ли кто-нибудь непрерывно обойти их, проходя только однажды через каждый  мост. И тут же мне было сообщено, что никто еще до сих пор не смог это проделать, но никто и не доказал, что это невозможно. Вопрос этот, хотя и банальный, показался мне, однако, достойным внимания тем, что для его решения недостаточны ни геометрия, ни алгебра, ни комбинаторное искусство. После долгих размышлений я нашел лёгкое правило, основанное на вполне убедительном доказательстве, с помощью которого можно во всех задачах такого рода тотчас же определить, может ли быть совершен такой обход через какое угодно число и как угодно расположенных мостов или не может“.  Кенигсбергские мосты схематически можно изобразить так.

Существует еще один вид задач, связанных с путешествиями  вдоль графов. Речь идёт о задачах, в которых требуется отыскать путь, проходящий через все вершины, причем не более одного раза через каждую. Цикл, проходящий через каждую вершину один и только один раз, носит название гамильтоновой линии( в честь Уильяма Роуэна Гамильтона, знаменитого ирландского математика прошлого века, который первым начал изучать такие линии). К сожалению, пока еще не найден общий критерий, с помощью которого можно было бы решить, является ли данный граф гамильтоновым, и если да, то найти на нём все гамильтоновы линии.

Сформули­рованная в середине 19 в. проблема четырех красоктакже выглядит как развле­кательная задача, однако попытки ее решения привели к появлению некоторыхисследований графов, имеющих теоретическое и прикладное значение. Проблема четырех красок формулируется так: ”Можно ли область любой плоской карты раскрасить четырьмя цветами так, чтобы любые две соседние области были раскрашены в различные цвета?”. Гипотеза о том, что ответ утвердительный, была сформулирована в середине 19в. В 1890 году было доказано более слабое утверждение, а именно, что любая плоская карта раскрашивается в пять цветов. Сопоставляя любой плоской карте двойственный ей плоский граф, получают эквивалентную формулировку задачи в терминах графов: Верно ли, что хроматическое число любого плоского графа меньше либо равно четырёх? Многочисленные попытки решения задачи оказали влияние на развитие ряда направлений теории графов. В 1976 году анонсировано положительное решение задачи с использованием ЭВМ.

I. Основныепонятиятеорииграфов.

1. Граф G(V,E) - комбинаторный объект, состоящий из двух конечных мно­жеств: V - называемого множеством вершин и множества пар элементов из V, т.е. Е VxV, называемого множеством ребер, если пары неупорядочены, и множеством дуг, если пары упорядочены. В первом случае граф G(V,E) называется неориентированным, во втором ориентированным. Если е = (v1,v2).

eЕ, то говорят, что ребро е соединяет вершиныv1,v2, если v1 =v2, то ребро е называет­ся петлей. Две вершины v1,v2 называются смежными, если существует соединяющее их ребро. Аналогично, два различных ребра смежны, если они имеют общую вершину.

Степенью вершины v называется число ребер d(v), инцидентных ей, при этом петля учитывается дважды. В случае ориентированного графа различают степень d0(v) по выходящим дугам и d1(v) - по входящим.

Путь - это последовательность ребер e1, е2, ... , еm, такая, что ei, ei+1 имеют об­щую вершину. Число ребер называется длиной пути. Если ни одна из вершин не появля­ется более одного раза, то путь называется простым. Ясно, что в простом пути ни одно ребро не используется дважды.

Путь называется циклом, если его начальная вершина совпадает с конечной, простым циклом, если это не выполняется для других вершин.

В случае ориентированного графа, если путь проходит в направлении дуг, он называется ориентированным. Аналогично определяется ориентированный цикл.

Граф называется связным, если для любых двух вершин существует путь, их со­единяющий. Ориентированный граф называется сильно связным, если для любых двух вершин существует ориентированный путь, их соединяющий. Для ориентированного графа определяем скелетный граф, как неориентированный граф, полученный снятием ориентации исходного графа.

3. Двудольные графы. Это графы, у которых множество вершин можно

разбить на два множества V1, и V2 , и так что каждое ребро графа соединяет только некоторую
вершину из V1 с некоторой вершиной изV2.

4. Граф единичного n-мерного куба Вn. Вершины графа - n-мерные двоичные наборы. Ребра соединяют вершины, отличающиеся одной координатой.

Факт 1. Любой граф содержит четное число вершин нечетной степени. ♦ Если граф G имеет xi вершинстепени i, то

X1+2x2+…+kxk=2E                                            (1)

поскольку мы подсчитываем число концевых вершин ребер, а каждое ребро имеет точно две концевые вершины. Отсюда получаем, что x1+ x3+ ... + x2s+1-  четное число.Число ребер в графе существенно влияет на его связность. Заметим, что любой граф можно разбить на связные части - компоненты связности, задав следующее отношение эквивалентности на множестве его вершин: две вершины эквивалентны, если существу­ет путь из одной вершины в другую. Таким образом, связный граф состоит из одной компоненты.

Факт 2. Пусть G - граф с n вершинами и k компонентами. Тогда число m его ребер удовлетворяет неравенствам:

              Нижнюю оценку доказывают индукцией по числу ребер в G. Если множество
ребер пусто, то утверждение очевидно. Если в графе G число ребер минимально (скажем m0), удаление любого ребра приводит к увеличению числа компонент на единицу. Зна­чит, в графе k+1 компонента иm0 -1 ребро. По предположению индукции , m0-1n-(k+1)откуда m0 > n - к. Для доказательства верхней оценки считаем каждую компоненту графа G полным графом. Если Ci и Cj - две компоненты с niи nj вершинами (ni > nj > 1), то заменяя их на полные графы с ni + 1 и nj -1 вершинами, мы, не меняя
числа вершин, увеличиваем число ребер. Действительно,

      Значит, максимальное число ребер имеет граф G , у которого k -1 изолированных вершин и компонента из полного графа на n - к + 1 вершинах. Отсюда и следует верхняя оценка.


Следствие. Любой граф с n вершинами, имеющий более, чем

                                                                                     ре­бер, связан.

                Действительно, если граф имеет k компонент, то по предыдущему, число его ребер не превышает

                Но неравенство:

справедливо только при к = 1.

Убедимся теперь в том, что степени вершин существенно влияют на наличие циклов в графе.

Факт 3. Если степень каждой вершины графа G(V,E) не меньше двух, то G содержит цикл.

   Пусть v - произвольная вершина из V. Строим последовательность ребер
(v,v1), (v1,v2), ..., выбирая v1 смежной с v, ... , Vi+1 - смежной с v1, и отличной от vi-1. По условию вершина Vi+1 существует. В силу конечности V на некотором шаге будет вы­брана вершина, уже встретившаяся раньше. Пусть это vk. Тогда часть последовательно­сти ребер между вхождениями vk образует цикл.

2.Пусть G - связный граф, u, v - произвольные вершины. Определим d(u, v) - расстояние между u и vкак длину кратчайшего пути из uв v. При этом полагаемd(u, v) = 0 при u = v.

Ясно, что введенное таким образом расстояние удовлетворяет аксиомам метри­ки:

1. d(u,v)

2. d(u, v) = 0

3. d(u,v) = d(v,u)

4. d(u, v)+d(v, w) d(u, w) (неравенство треугольника)
Для связного графа G диаметр d(G) определяется как`          

d(G) = maxd(u,v)

3.Графы G1(V1, E1) и G2(V2, E2) называются изоморфными, если существует биекция f: V1V2, такая, что выполнено

(v1, v2)(f(v1), f(v2)2

При этом f называется изоморфизмом графов G1 и G2. Изоморфизм графа G на себя называется автоморфизмом.

Пример 1. Следующие графы имеют только тождественные автоморфмы




Пример 2. Следующий граф имеет, кроме тождественного, автоморфизмы (1,3), (2,4), (13)(24).

Широко известна так называемая проблема изоморфизма графов, в которой для любых двух графов требуется установить, изоморфны они или нет. Для знакомства с результатами по данной проблеме следует обратиться к приведенному списку литерату­ры.

4. Поскольку графы можно рассматривать как частные случаи бинарных отно­шений, то для них могут быть определены аналогичные операции. Укажем некоторые из них.

Пусть G1 + (V1, E1), G2 = (V2, E2) - два графа.

Объединение графов G1 и G2 есть граф, у которого V = V1 V2,

Е = E1 Е2.

Соединение графов G1+G2 есть граф, у которого

V = V1 V2, Е = E1 Е2{(v1, v2)} для всех v1V1, v2V2

Прямое произведение графов есть граф, у которого V = V1V2,

((c1,v2),(v1,v2))(v1,v1)и (v2,v2)E2

Пример. Пусть даны графы отображений f1 V1Vi, f2: V2V2. Тогда пря­
мое   произведение      соответствует      отображению
f1f2: VV2 V1V2 где f1f2(v1,v2) = (f1,(v1), f2(v2))

Пусть f1 и f2  имеют    и    начальных вершин соответственно. Тогда f1f2 будет

иметь

Некоторые классы графов допускают характеристическое описание. В качестве примера приведем критерий двудольности графа (Кёниг, 1936 г.)

Теорема. Для двудольности графа необходимо и достаточно, чтобы он не со­держал циклов нечетной длины.

Пусть G = (V, Е) - двудольный граф, С - один из его циклов длины k. Фикси­руем вершину v1 и проходим цикл, начиная с v1. Пусть это вершины v1, v2,..., vk. Поскольку концы каждого ребра лежат в разных долях, то k - четное число.

Пусть G = (V, Е) - связный и все его циклы четной длины. Определим разбиение V = V1V2 следующим образом: Фиксируем произвольную вершину v1V и включа­ем ее в V1. Теперь включаем u1d(u, v1) - четное число. Остальные вершины включаем в V2.

Покажем, что граф G двудольный. Пусть, напротив, существует ребро (v', v"), где v', v" V1. Следовательно, d(v1, v'), d(v1, v") - четны. Ребро (v', v") дает цикл нечет­ной длины, содержащий путь от v1 к v', ребро (v', v"), путь от v" к v1. Аналогично пока­зываем, что нет ребер (v', v"), v', v" V2.

1. Эйлеровыграфы.

Эйлеровым путем графа G(V,E) называется путь e1,e2, ..., et такой, что каждое ребро появляется ровно 1 раз, т.е. t = | Е |. Граф G(V,E) называется эйлеровым, если он имеет замкнутый эйлеровый путь, и полуэйлеровым, если существует эйлеров путь, не являющийся замкнутым.

Теорема 1. Связный граф G является эйлеровым тогда и только тогда, когда ка­ждая вершина G имеет четную степень.

Предположим, что Р является эйлеровым циклом в графе G. Тогда при всяком прохождении цикла через любую вершину графа используется одно ребро для входа и одно ребро для выхода. Поскольку каждое ребро используется один раз, то каждая вер­шина должна иметь четную степень. Обратное утверждение доказываем индукцией по числу ребер в графе G. Пусть граф G связен и степень каждой вершины четна. На осно­вании Факта 3 граф содержит цикл C. Если C содержит каждое ребро, то все доказано. Если же нет, то удаляем из графа Gвсе ребра, принадлежащие циклу C. Получаем но­вый граф G1, возможно несвязный. Число ребер в G1 меньше чем в G, и каждая вершина имеет четную степень. По индуктивному предположению в каждой компоненте графа d имеется эйлеров цикл. В силу связности графа G каждая компонента графа G1 имеет общие вершины с циклом С. Теперь проходим, ребра графа G следующим образом: идем по ребрам цикла С до первой неизолированной вершины графа G1. Затем проходим эй­леров цикл в компоненте графа G1, затем снова двигаемся по циклу С до следующей неизолированной вершины графа G1. Ясно, что процесс заканчивается в исходной вер­шине, что и показывает существование эйлерова цикла.

Аналогичным образом доказывается

Теорема 2. Связный граф G является полуэйлеровым тогда и только тогда, когда в нем существует точно две вершины нечетной степени.Аналогичное определение можно сделать для ориентированных графов. Ориентированный эйлеров путь это ориен­тированный путь, содержащий каждую дугу точно один раз. Ориентированный граф называется эйлеровым, если в нем существует ориентированный эйлеров путь.

Аналогично теореме 1 можно доказать следующее утверждение.

Теорема 3. Ориентированный граф G(V,E), у которого связан соответствующий скелетный граф, является Эйлеровым тогда и только тогда, когда либо для всех вершин v, di(v) = d0(v), либо существуют точно две вершины v1 и v2 такие, что d0(v1) = di(v1) + 1,

d0(v2) + 1 = di(v2), а для остальных вершин

dI(v) = d0(v).                                                                 (3)

В первом случае любой эйлеров путь является ориентированным циклом, во втором -

начинается в вершине v1 заканчивается в вершине v2

Теорема 4. Пусть G - связный граф, имеющий точно 2s > 0 вершин нечетной степени. Тогда существует s и не существует меньшего числа путей P1, ... , Ps, которые в совокупности содержат все ребра графа G точно по одному разу. При этом каждый из путей P1, ..., Ps начинается в одной нечетной вершине и кончается в другой.

Согласно факта 1 в графе G имеется четное число 2s вершин нечетной степе­ни. Разобьем эти вершины на s пар (v1, w1), ..., (vs, ws). Образуем теперь новый граф G1,= добавив каждой паре (vi, wi), i = 1,s ребро. Тогда G - связный граф, у которого все вер­шины четны. Согласно теореме 1 в графе G1 существует эйлеров цикл С, проходящий по всем ребрам точно по одному разу. Удалим из цикла С добавленные ребра и получим sпутей P1, ..., Ps, проходящих каждое ребро точно один раз. Ясно, что каждый путь на­чинается и кончается в нечетной вершине. Пусть теперь имеется t путей t < sP1, ... , Pt, содержащих все ребра графа G. Тогда каждая нечетная вершина должна быть концом пути и, значит, имея 2s нечетных вершин, нельзя покрыть все ребра графа G менее, чем sпутями.

Приведем теперь алгоритм построения эйлерового пути в данном эйлеровом графе.

Теорема 5. Пусть G - эйлеров граф. Тогда следующая процедура всегда возмож­на и приводит к построению эйлеровой цепи графа G.

Выходя из произвольной вершины, идем по ребрам графа произвольным обра­зом, соблюдая следующие правила:

1) стираем ребра по мере их прохождения (вместе с изолированными вершина­ми, которые при этом образуются);

2)на каждом этапе идем по ребру, удаление которого нарушает связность, толь­ко в том случае, когда нет других возможностей.

Убедимся сначала, что указанная процедура может быть       выполнена на каж­дом этапе. Пусть мы достигли некоторой вершины v, начав с вершины u, vu. Удалив ребра пути из v в u, видим,

чтооставшийся граф G1 связен и содержит ровно две нечет­ных вершины

v и u. Согласно теореме 2 граф G1 имеет эйлеров путь Р из v в и. Посколь­ку удаление первого ребра инцидентного u пути P либо не нарушает связности G1, либо происходит удаление вершины u и оставшийся граф G2 связен с двумя нечетными вер-

шинами, то отсюда получаем, что описанное выше построение всегда возможно на каж­дом шаге. (Если v = и, то доказательство не меняется, если имеются ребра, инцидентные u). Покажем, что данная процедура приводит к эйлерову пути. Действительно, в G не может быть ребер, оставшихся непройденными после использования последнего ребра, инцидентного u, поскольку в противном случае удаление ребра, смежному одному из оставшихся, привело бы к несвязному графу, что противоречит 2). ♦

В качестве одного из применений эйлеровых графов приведем следующее.

Пусть А = {0, 1, ..., m-1} - алфавит из m букв. Ясно, что имеется

mn,различных слов длины n в алфавите А. Последовательностью де Брейна называется циклическое слово a0 a1…aL-1         в алфавите А, такое, что подпоследовательности     вида         aiai+1…ai+n-1 i = 0, ..., L-1 состоят из всех возможных L = mn слов длины n. Наиболее важный случай для приложений m = 2. Последовательности де Брейна производятся полноцикловыми регистрами сдвига. Покажем существование последовательностей де Брейна.

Пример.

Определим ориентированный граф Gm,n(V,E) следующим образом

1) V является множеством всех mn-1 слов длины n-1 над A

2) Е является множеством всех mnслов длины nнад A

3) дуга (a1, a2 … ,an) имеет начальной вершиной (a1, … ,an-1) и конечной (an, … ,an).

Приведем граф G2,3 :  

Ясно, что последовательности де Брейна соответствует замкнутый путь в графе Gm,n содержащий каждую дугу точно один раз. Обратно, ориентированный цикл в Gm,n, содержащий каждую дугу точно один раз, приводит к построению цикла де Брейна, если выписывать соответствующие дуги подряд.

Пример. Для графа G2,3. имеем эйлеров путь

000, 001, 011, 111, 110, 101, 010, 100, а соответствующую   последовательность де Брейна

00011101

Теорема 6. Для любых целых mи n граф Gm,n имеет ориентирован-

ный эйлеров цикл.

           Покажем сначала, что граф Gm,nсильно связен, а значит его соответствующий скелетный граф связен. Действительно, пусть b1, ... , bn-1

и c1, ..., cn-1 две вершины. То­гда их соединяет следующий ориентированный путь

(b1, b2, ..., bn-1, c1), (b2, ... , bn-1, c1, c2), ... , (bn-1, c1, ..., cn-1).

Далее dI(v) = d0(v) = mдля любой вершины v.

Действительно, из вершины v = (b1, b2, ..., bn-1) выходят дуги вида:

           (b1, b2, ..., bn-1)

и входят дуги вида (с, b1 ... , bn-1), с А.

Теперь по теореме 3 в графе Gm,n существуют эйлеровы циклы.

Следствие. Для любых целых m, n последовательности де Брейна существуют.


Теорема 7. Для любых натуральных m, n существует точно

последовательностей де Брейна.

2. Кратчайшие пути.

Пусть G(V,E) - конечный неориентированный граф и пусть заданы две его вер­шины s и t. Требуется найти кратчайший путь (длина пути равна числу входящих в него ребер) от вершины s к вершине t. Сначала мы опишем алгоритм, который находит длину кратчайшего пути.

Алгоритм ДЛИНА

1) Помечаем вершину s пометкой 0. Полагаем i = 0.

2)Находим все непомеченные вершины, связанные ребром с

вершина­ми, имеющими отметку i. Если таких вершин нет, t недостижимо из s,. Ес­ли такие вершины есть, помечаем их i+1.

              3)Если вершина t помечена, переходим к 4). Если нет, то                                           увеличиваем I на 1 и повторяем шаг 2).

4)Длина кратчайшего пути от s к t равна i+1, стоп.
Корректность алгоритма следует из следующего утверждения.

Факт 1. Вершина v графа G(V,E) помечается в алгоритме пометкой v) тогда и только тогда, когда длина кратчайшего пути от вершины s к v равна (v).

♦ Доказательство индукцией по i. Ясно, что при i = 0,(v) = 0 влечет v = s и ут­верждение справедливо. Предположим, что утверждение верно для всех вершин v, для которых (v) m. Если вершина и не помечена, значит, нет пути от sк u, меньше чем m+1. Если u связана ребром с вершиной, помечной,то ее пометка, во-первых , будет равна m+1 , во-вторых , имеется путь длины m от s к данной вершине и, значит, длина кратчайшего пути от sк u равна m+1. Если uне связана ребром с вершиной, имеющей пометку m, то не существует пути, короче, чем m+1 от sк u, поскольку предыдущая вершина на этом пути имела бы

пометку m.

Алгоритм ПУТЬ.

1) Полагаем i = (t) и помечаем v(i) = t.

2)Находим вершину uтакую, что u связана ребром с v(i) и (u) = i-1. Помечаемv(i-1) = u.

3) Еслиi = 1, то останавливаемся, и уменьшаем i на 1 и повторяем шаг 2). ♦
Приводимое ниже утверждение позволяет находить число путей фиксированной длины
между любыми двумя вершинами.

Для графа G(V,E), | V| = u определим матрицу смежности, т.е. (n) - матрицу A = (aij), i,j = l, ... ,u,где

3.Деревья.

1. Связный граф G(V, E), не имеющий циклов, называется деревом. Следующая теорема перечисляет некоторые основные свойства деревьев.

Теорема 1. Пусть граф G(V, E) имеет п вершин. Тогда следующие утверждения эквиваленты.

1) G является деревом;

2)G не содержит циклов и имеет n -1 ребер;

3) Gсвязен и имеет n - 1ребер;

4)G связен, но удаление любого ребра нарушает связность;

5) любые две вершины графа G соединены ровно одним путем;

6) G не имеет циклов, но добавление любого ребра порождает ровно один цикл.

♦ При n = 1 утверждение очевидно, поэтому считаем n2. 1) => 2). По опреде­лению G не имеет циклов. Рассмотрим некоторое ребро = (v1, v2) и удалим его. Полу­чим граф G'. В графе G' нет пути из v1 в v2 , т.к. если бы такой путь был, то в графе Gбыл бы цикл. Значит G' не связен и не имеет циклов. Значит он состоит из двух компо­нент, являющихся деревьями с числом вершин n1 и n2 соответственно (n1 + n2 = n). По индуктивному предположению G' имеет     n1 -1 + n2 -1 ребер. Следовательно, граф Gимеет n -1 ребер.

2)=> 3). Если бы G был несвязен, то каждая его компонента представляла бы собой связный граф без циклов. Из предыдущего имеем, что число ребер в каждой ком­поненте меньше на одинo числj ее вершин. Значит, общее число ребер меньше числа вершин по крайней мере на два, что противоречит тому, что G имеет п - 1ребер.

3) => 4). Удаление любого ребра приводит к графу с n вершинами и n-2 ребрами,
который не может быть связным.

4)=> 5). В силу связности G, каждая пара вершин соединена путем. Если бы данная пара была соединена более, чем одним путем, то они образовывали бы цикл. Но тогда удаление любого ребра в цикле не нарушает связности графа.

5) => 6). Если бы G содержал цикл, то любые две вершины на цикле соединя­лись бы по крайней мере двумя путями. Добавим теперь к графу G ребро = (v1, v2).
Тогда образуется цикл, т.к. вершины v1 и v2 уже соединены путем. Ясно, что цикл един­ственный.

6) => 1). Если бы G был несвязен, то добавление ребер, соединяющих вершины из разных компонент, не приводит к образованию цикла. ♦

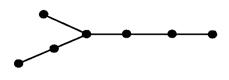
Следствие. Дерево с более чем одной вершиной имеет по крайней мере две вер­шины степени 1.

♦ Действительно, пусть v1, ..., vn - множество вершин, тогда имеем

               

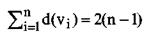
В силу связности d(vi) 1 , отсюда и следует утверждение. ♦

2. Для графа G(V, E) определим два полезные понятия.

Вершинный подграфG(V', E') - это граф на множестве вершин              Е'Eребра­ми Е' Е, такими, что оба конца ребра е' Е' принадлежат V.

Реберный подграфG(V, E') - это граф, определяемый подмножеством ребер Е'Eмножеством вершин VV, состоящим из концевых вершин ребер из Е'. Остовным (покрывающим) деревом графа G(V, E) называется его реберный подграф с множе­ством вершин V, являющийся деревом.

Факт 2. Граф G(V, E) имеет остовное дерево тогда и только тогда, когда он свя­зен. ♦ Предложим процедуру построения остовного дерева. Ясно, что если граф G не связен, то он не может иметь остовного дерева.

Пусть граф связен. Если в графе нет ребра, удаление которого сохраняет связ­ность графа, то G - дерево.

Если такое ребро есть, удалим его и продолжим процедуру. Когда процедура не может быть продолжена, полученный граф является деревом.


Рассмотрим теперь известную проблему нахождения минимального остовного дерева. Пусть G(V, E) неориентированный граф и пусть каждому ребру е поставлено в соответствие положительное число (е), называемое его весом. Требуется найти связ­ный реберный подграф G'(V’, E'), такой, что V’ = V, причем сумма

минимальна.

Ясно, что граф G(V, E') должен быть деревом. Действительно, если G(V', E') содержит цикл, то тогда любое ребро цикла можно удалить из графа и тем самым уменьшить сум­марный вес ребер графа G(V’, E').

II. Задача коммивояжера

1. Общее описание

Задача коммивояжера (в дальнейшем сокращённо - ЗК) является одной из знаменитых задач теории комбинаторики. Она была поставлена в 1934 году, и об неё, как об Великую теорему Ферма обламывали зубы лучшие математики. В своей области (оптимизации дискретных задач) ЗК служит своеобразным полигоном, на котором испытываются всё новые методы.

Постановка задачи следующая.

Коммивояжер (бродячий торговец) должен выйти из первого города, посетить по разу в неизвестном порядке города 2,1,3..n и вернуться в первый город. Расстояния между городами известны. В каком порядке следует обходить города, чтобы замкнутый путь (тур) коммивояжера был кратчайшим?

Чтобы привести задачу к научному виду, введём некоторые термины. Итак, города перенумерованы числами jÎТ=(1,2,3..n). Тур коммивояжера может быть описан циклической перестановкой t=(j1,j2,..,jn,j1), причём все j1..jn – разные номера; повторяющийся в начале и в конце j1, показывает, что перестановка зациклена. Расстояния между парами вершинСijобразуют матрицу С. Задача состоит в том, чтобы найти такой тур t, чтобы минимизировать функционал

                         

Относительно математизированной формулировки ЗК уместно сделать два замечания.

Во-первых, в постановке Сijозначали расстояния, поэтому они должны быть неотрицательными, т.е. для всех jÎТ:

                                            Сij³0; Cjj=∞

(последнее равенство означает запрет на петли в туре), симметричными, т.е.для всех i,j:

                                               Сij= Сji.

и удовлетворять неравенству треугольника, т.е. для всех:

                       Сij+ Сjk³Cik

В математической постановке говорится о произвольной матрице. Сделано это потому, что имеется много прикладных задач, которые описываются основной моделью, но всем условиям (2)-(4) не удовлетворяют. Особенно часто нарушается условие (3) (например, если Сij – не расстояние, а плата за проезд: часто туда билет стоит одну цену, а обратно – другую). Поэтому мы будем различать два варианта ЗК: симметричную задачу, когда условие (3) выполнено, и несимметричную - в противном случае. Условия (2)-(4) по умолчанию мы будем считать выполненными.

Второе замечание касается числа всех возможных туров. В несимметричной ЗК все туры t=(j1,j2,..,jn,j1) и t’=(j1,jn,..,j2,j1) имеют разную длину и должны учитываться оба. Разных туров очевидно (n-1)!.

Зафиксируем на первом и последнем месте в циклической перестановке номер j1, а оставшиеся n-1 номеров переставим всеми (n-1)! возможными способами. В результате получим все несимметричные туры. Симметричных туров имеется в два раз меньше, т.к. каждый засчитан два раза: как t и как t’.

Можно представить, что С состоит только из единиц и нулей. Тогда С можно интерпретировать, как граф, где ребро (i,j)проведено, если Сij=0 и не проведено, если Сij=1. Тогда, если существует тур длины 0, то он пройдёт по циклу, который включает все вершины по одному разу. Такой цикл называется гамильтоновым циклом. Незамкнутый гамильтонов цикл называется гамильтоновой цепью (гамильтоновым путём).

В терминах теории графов симметричную ЗК можно сформулировать так:

Дана полная сеть с nвершинами, длина ребра (i,j)= Сij. Найти гамильтонов цикл минимальной длины.

В несимметричной ЗК вместо “цикл” надо говорить “контур”, а вместо “ребра” - “дуги” или “стрелки”.

Некоторые прикладные задачи формулируются как ЗК, но в них нужно минимизировать длину не гамильтонова цикла, а гамильтоновой цепи. Такие задачи называются незамкнутыми. Некоторые модели сводятся к задаче о нескольких коммивояжерах, но мы здесь их рассматривать не будем.

2. Методы решения ЗК

a. Жадный алгоритм

         Жадный алгоритм – алгоритм нахождения наикратчайшего расстояния путём выбора самого короткого, ещё не выбранного ребра, при условии, что оно не образует цикла с уже выбранными рёбрами. “Жадным” этот алгоритм назван потому, что на последних шагах приходится жестоко расплачиваться за жадность.

Посмотрим, как поведет себя при решении ЗК жадный алгоритм. Здесь он превратится в стратегию “иди в ближайший (в который еще не входил) город”. Жадный алгоритм, очевидно, бессилен в этой задаче. Рассмотрим для примера сеть на рис. 2, представляющую узкий ромб. Пусть коммивояжер стартует из города 1. Алгоритм “иди вы ближайший город” выведет его в город 2, затем 3, затем 4; на последнем шаге придется платить за жадность, возвращаясь по длинной диагонали ромба. В результате получится не кратчайший, а длиннейший тур.

            В пользу процедуры “иди в ближайший” можно сказать лишь то, что при старте из одного города она не уступит стратегии “иди в дальнейший”.

            Как видим, жадный алгоритм ошибается. Можно ли доказать, что он ошибается умеренно, что полученный им тур хуже минимального, положим, в 1000 раз? Мы докажем, что этого доказать нельзя, причем не только для жадного логарифма, а для алгоритмов гораздо более мощных. Но сначала нужно договориться, как оценивать погрешность неточных алгоритмов, для определенности, в задаче минимизации. Пусть fB- настоящий минимум, а         fA - тот квазиминимум, который получен по алгоритму. Ясно, что fA/fB≥1, но это – тривиальное утверждение, что может быть погрешность. Чтобы оценить её, нужно зажать отношение оценкой сверху:

                             fA/fB ≥1+ nε,

где, как обычно в высшей математике, ε≥0, но, против обычая, может быть очень большим. Величина ε и будет служить мерой погрешности. Если алгоритм минимизации будет удовлетворять неравенству (5), мы будем говорить, что он имеет погрешность ε.

         Предположим теперь, что имеется алгоритм А решения ЗК, погрешность которого нужно оценить. Возьмем произвольный граф G (V,E) и по нему составим входную матрицу ЗК:

С[i,j]={

1,если ребро (i,j) принадлежит Е

1+nε  в противном случае

Если в графе G есть гамильтонов цикл, то минимальный тур проходит по этому циклу и fB = n. Если алгоритм А тоже всегда будет находить этот путь, то по результатам алгоритма можно судить, есть ли гамильтонов цикл в произвольном графе. Однако, непереборного алгоритма, который мог бы ответить, есть ли гамильтонов цикл в произвольном графе, до сих пор никому не известно. Таким образом, наш алгоритм А должен иногда ошибаться и включать в тур хотя бы одно ребро длины 1+nε. Но тогда fA³(n-1)+(1+nε) так что fA/fB=1+nε т.е. превосходит погрешность ε на заданную неравенством (5). О величине ε в нашем рассуждении мы не договаривались, так что ε может быть произвольно велик.

Таким образом доказана следующая теорема.

         Либо алгоритм А определяет, существует ли в произвольном графе гамильтонов цикл, либо погрешность А при решении ЗК может быть произвольно велика.

         Это соображение было впервые опубликовано Сани и Гонзалесом в 1980 г. Теорема Сани-Гонзалеса основана на том, что нет никаких ограничений на длину ребер. Теорема не проходит, если расстояния подчиняются неравенству треугольника (4).

Если оно соблюдается, можно предложить несколько алгоритмов с погрешностью 12. Прежде, чем описать такой алгоритм, следует вспомнить старинную головоломку. Можно ли начертить одной линией открытый конверт? Рис.2 показывает, что можно (цифры на отрезках показывают порядок их проведения). Закрытый конверт (рис.3.) одной линией нарисовать нельзя и вот почему. Будем называть линии ребрами, а их перекрестья – вершинами.

Когда через точку проводится линия, то используется два ребра – одно для входа в вершину, одно – для выхода. Если степень вершины нечетна – то в ней линия должна начаться или кончиться. На рис. 3 вершин нечетной степени две: в одной линия начинается, в другой – кончается. Однако на рис. 4 имеется четыре вершины степени три, но у одной линии не может быть четыре конца. Если же нужно прочертить фигуру одной замкнутой линией, то все ее вершины должны иметь четную степень.

         Верно и обратное утверждение: если все вершины имеют четную степень, то фигуру можно нарисовать одной незамкнутой линией. Действительно, процесс проведения линии может кончиться, только если линия придет в вершину, откуда уже выхода нет: все ребра, присоединенные к этой вершине (обычно говорят: инцидентные этой вершине), уже прочерчены. Если при этом нарисована вся фигура, то нужное утверждение доказано; если нет, удалим уже нарисованную часть G’. После этого от графа останется одна или несколько связных компонент; пусть G’ – одна из таких компонент. В силу связности исходного графа G, G’ и G’’ имеют хоть одну общую вершину, скажем,v. Если в G’’ удалены какие-то ребра, то по четному числу от каждой вершины. Поэтому G’’ – связный и все его вершины имеют четную степень. Построим цикл в G’’ (может быть, не нарисовав всего G’’) и через v добавим прорисованную часть G’’ к G’. Увеличивая таким образом прорисованную часть G’, мы добьемся того, что G’ охватит весь G.

         Эту задачу когда-то решил Эйлер, и замкнутую линию, которая покрывает все ребра графа, теперь называю эйлеровым циклом. По существу была доказана следующая теорема.

         Эйлеров цикл в графе существует тогда и только тогда, когда (1) граф связный и (2) все его вершины имеют четные степени.

б. Деревянный алгоритм.

         Теперь можно обсудить алгоритм решения ЗК через построение кратчайшего остовного дерева. Для краткости будет называть этот алгоритм деревянным.

         Вначале обсудим свойство спрямления. Рассмотрим какую-нибудь цепь, например, на рис.5. Если справедливо неравенство треугольника, то d[1,3]£d[1,2]+d[2,3] и d[3,5]£d[3,4]+d[4,5]                                                       Сложив эти два неравенства, получим d[1,3]+d[3,5]£d[1,2]+d[2,3]+d[3,4]+d[4,5]. По неравенству треугольника получим. d[1,5]£d[1,3]+d[3,5]. Окончательно

d[1,5]£d[1,2]+d[2,3]+d[3,4]+d[4,5]

         Итак, если справедливо неравенство треугольника, то для каждой цепи верно, что расстояние от начала до конца цепи меньше (или равно) суммарной длины всех ребер цепи. Это обобщение расхожего убеждения, что прямая короче кривой.

         Вернемся к ЗК и опишем решающий ее деревянный алгоритм.

1.Построим на входной сети ЗК кратчайшее остовное дерево и удвоим все его ребра. Получим граф G – связный и с вершинами, имеющими только четные степени.

2.Построим эйлеров цикл G, начиная с вершины 1, цикл задается перечнем вершин.

3.Просмотрим перечень вершин, начиная с 1, и будем зачеркивать каждую вершину, которая повторяет уже встреченную в последовательности. Останется тур, который и является результатом алгоритма.

Пример 1. Дана полная сеть, показанная на рис.5. Найти тур жадным и деревянным алгоритмами.

-

1

2

3

4

5

6

1

-

6

4

8

7

14

2

6

-

7

11

7

10

3

4

7

-

4

3

10

4

8

11

4

-

5

11

5

7

7

3

5

-

7

6

14

10

10

11

7

-

табл. 1

Решение. Жадный алгоритм (иди в ближайший город из города 1) дает тур 1–(4)–3-(3)–5(5)–4–(11)–6–(10)–2–(6)–1, где без скобок показаны номера вершин, а в скобках – длины ребер. Длина тура равна 39, тур показана на рис. 5.

2. Деревянный алгоритм вначале строит остовное дерево, показанное на рис. 6 штриховой линией, затем эйлеров цикл 1-2-1-3-4-3-5-6-5-3-1, затем тур 1-2-3-4-5-6-1 длиной 43, который показан сплошной линией на рис. 6.

Теорема. Погрешность деревянного алгоритма равна 1.

Доказательство. Возьмем минимальный тур длины fBи удалим из него максимальное ребро. Длина получившейся гамильтоновой цепи LHC меньше fB. Но эту же цепь можно рассматривать как остовное дерево, т. к. эта цепь достигает все вершины и не имеет циклов. Длина кратчайшего остовного дереваLMT меньше или равна LHC. Имеем цепочку неравенств

fB>LHC³LMT

(6)

Но удвоенное дерево – оно же эйлеров граф – мы свели к туру посредством спрямлений, следовательно, длина полученного по алгоритму тура удовлетворяет неравенству

2LMT>fA

(7)

Умножая (6) на два и соединяя с (7), получаем цепочку неравенств

2fB>2LHC³2LMT³fA

(8)

Т.е. 2fB>fA, т.е. fA/fB>1+e; e=1.

Теорема доказана.

   Таким образом, мы доказали, что деревянный алгоритм ошибается менее, чем в два раза. Такие алгоритмы уже называют приблизительными, а не просто эвристическими.

Известно еще несколько простых алгоритмов, гарантирующих в худшем случае e=1. Для того, чтобы найти среди них алгоритм поточнее, зайдем с другого конца и для начала опишем “brute-forceenumeration” - “перебор животной силой”,как его называют в англоязычной литературе. Понятно, что полный перебор практически применим только в задачах малого размера. Напомним, что ЗК с n городами требует при полном переборе рассмотрения (n-1)!/2 туров в симметричной задаче и (n-1)! Туров в несимметричной, а факториал, как показано в следующей таблице, растет удручающе быстро:

5!

10!

15!

20!

25!

30!

35!

40!

45!

50!

~102

~106

~1012

~1018

~10125

~1032

~1040

~1047

~1056

~1064

            Чтобы проводить полный перебор в ЗК, нужно научиться (разумеется, без повторений) генерировать все перестановки заданного числа m элементов. Это можно сделать несколькими способами, но самый распространенный (т.е. приложимый для переборных алгоритмов решения других задач) – это перебор в лексикографическом порядке.

         Пусть имеется некоторый алфавит и наборы символов алфавита (букв), называемые словами. Буквы в алфавите упорядочены: например, в русском алфавите порядок букв аµбµя (символ µ читается “предшествует)”. Если задан порядок букв, можно упорядочить и слова. Скажем, дано слово u=(u1,u2,..,um) – состоящее из букв u1,u2,..,um - и слово v =(v1,v2,..,vb). Тогда если u1µv1, то и uµv, если же u1=v1, то сравнивают вторые буквы и т.д. Этот порядок слов и называется лексикографическим. Поэтому в русских словарях (лексиконах) слово “абажур” стоит раньше слова “абака”. Слово “бур” стоит раньше слова “бура”, потому что пробел считается предшествующим любой букве алфавита.

         Рассмотрим, скажем, перестановки из пяти элементов, обозначенных цифрами 1..5. Лексикографически первой перестановкой является 1-2-3-4-5, второй – 1-2-3-5-4, …, последней – 5-4-3-2-1. Нужно осознать общий алгоритм преобразования любой перестановки в непосредственно следующую.

            Правило такое: скажем, дана перестановка 1-3-5-4-2. Нужно двигаться по перестановке справа налево, пока впервые не увидим число, меньшее, чем предыдущее (в примере это 3 после 5). Это число, Pi-1 надо увеличить, поставив вместо него какое-то число из расположенных правее, от Pi до Pn. Число большее, чем Pi-1, несомненно, найдется, так как                 Pi-1< Pi . Если есть несколько больших чисел, то, очевидно, надо ставить меньшее из них. Пусть это будет Pj,j>i-1. Затем число Pi-1 и все числа от Pi до Pn, не считая Pj нужно упорядочить по возрастанию. В результате получится непосредственно следующая перестановка, в примере –   1-4-2-3-5. Потом получится 1-4-2-5-3 (тот же алгоритм, но упрощенный случай) и т.д.

         Нужно понимать, что в ЗК с n городами не нужны все перестановки из n элементов. Потому что перестановки, скажем, 1-3-5-4-2 и 3-5-4-2-1 (последний элемент соединен с первым) задают один и тот же тур, считанный сперва с города 1, а потом с города 3. Поэтому нужно зафиксировать начальный город 1 и присоединять к нему все перестановки из остальных элементов. Этот перебор даст (n-1)! разных туров, т.е. полный перебор в несимметричной ЗК (мы по-прежнему будем различать туры 1-3-5-4-2 и 1-2-4-5-3).

         Данный алгоритм описан на языке Паскаль (см. Приложения).

Пример 2. Решим ЗК, поставленную в Примере 1 лексикографическим перебором. Приведенная выше программа напечатает города, составляющие лучший тур: 1-2-6-5-4-3 и егодлину 36.

Желательно усовершенствовать перебор, применив разум. В следующем пункте описан алгоритм, который реализует простую, но широко применимую и очень полезную идею.

в. Метод ветвей и границ

         К идее метода ветвей и границ приходили многие исследователи, но Литтл с соавторами на основе указанного метода разработали удачный алгоритм решения ЗК и тем самым способствовали популяризации подхода. С тех пор метод ветвей и границ был успешно применен ко многим задачам, для решения ЗК было придумано несколько других модификаций метода, но в большинстве учебников излагается пионерская работа Литтла.

           Общая идея тривиальна: нужно разделить огромное число перебираемых вариантов на классы и получить оценки (снизу – в задаче минимизации, сверху – в задаче максимизации) для этих классов, чтобы иметь возможность отбрасывать варианты не по одному, а целыми классами. Трудность состоит в том, чтобы найти такое разделение на классы (ветви) и такие оценки (границы), чтобы процедура была эффективной.

-

1

2

3

4

5

6

1

-

0

0

3

3

6

2

0

-

1

4

1

0

3

1

2

-

0

0

3

4

4

5

0

-

1

3

5

4

2

0

1

-

0

6

7

1

3

3

0

-

2

1

4

табл. 4

         Изложим алгоритм Литтла на примере 1 предыдущего раздела.. Повторно запишем матрицу:

-

1

2

3

4

5

6

1

-

6

4

8

7

14

2

6

-

7

11

7

10

3

4

7

-

4

3

10

4

8

11

4

-

5

11

5

7

7

3

5

-

7

6

14

10

10

11

7

-

табл. 2

-

1

2

3

4

5

6

1

-

2

0

4

3

10

4

2

0

-

1

5

1

4

6

3

1

4

-

1

0

7

3

4

4

7

0

-

1

7

4

5

4

4

0

2

-

4

3

6

7

3

3

4

0

-

7

табл. 3

Нам будет удобнее трактовать Сij как стоимость проезда из города i в город j. Допустим, что добрый мэр города j издал указ выплачивать каждому въехавшему в город коммивояжеру 5 долларов. Это означает, что любой тур подешевеет на 5 долларов, поскольку в любом туре нужно въехать в город j. Но поскольку все туры равномерно подешевели, то прежний минимальный тур будет и теперь стоить меньше всех. Добрый же поступок мэра можно представить как уменьшение всех чисел j-го столбца матрицы С на 5. Если бы мэр хотел спровадить коммивояжеров изj-го города и установил награду за выезд в размере 10 долларов, это можно было бы выразить вычитанием 10 из всех элементов j-й той строки. Это снова бы изменило стоимость каждого тура, но минимальный тур остался бы минимальным. Итак, доказана следующая лемма.

         Вычитая любую константу из всех элементов любой строки или столбца матрицы С, мы оставляем минимальный тур минимальным.

            Для алгоритма нам будет удобно получить побольше нулей в матрице С, не получая там, однако, отрицательных чисел. Для этого мы вычтем из каждой строки ее минимальный элемент (это называется приведением по строкам, см. табл. 3), а затем вычтем из каждого столбца матрицы, приведенной по строкам, его минимальный элемент, получив матрицу, приведенную по столбцам, см. табл. 4).

         Прочерки по диагонали означают, что из города i в город i ходить нельзя. Заметим, что сумма констант приведения по строкам равна 27, сумма по столбцам 7, сумма сумм равна 34.

         Тур можно задать системой из шести подчеркнутых (выделенных другим цветом) элементов матрицы С, например, такой, как показано на табл. 2. Подчеркивание элемента       означает, что в туре из i-го элемента идут именно в j-тый. Для тура из шести городов подчеркнутых элементов должно быть шесть, так как в туре из шести городов есть шесть ребер. Каждый столбец должен содержать ровно один подчеркнутый элемент(в каждый город коммивояжер въехал один раз), в каждой строке должен быть ровно один подчеркнутый элемент (из каждого города коммивояжер выехал один раз); кроме того, подчеркнутые элементы должны описывать один тур, а не несколько меньших циклов. Сумма чисел подчеркнутых элементов есть стоимость тура. На табл. 2 стоимость равна 36, это тот минимальный тур, который получен лексикографическим перебором.

         Теперь будем рассуждать от приведенной матрицы на табл. 2. Если в ней удастся построить правильную систему подчеркнутых элементов, т.е. систему, удовлетворяющую трем вышеописанным требованиям, и этими подчеркнутыми элементами будут только нули, то ясно, что для этой матрицы мы получим минимальный тур. Но он же будет минимальным и для исходной матрицы С, только для того, чтобы получить правильную стоимость тура, нужно будет обратно прибавить все константы приведения, и стоимость тура изменится с 0 до 34. Таким образом, минимальный тур не может быть меньше 34. Мы получили оценку снизу для всех туров.

         Теперь приступим к ветвлению. Для этого проделаем шаг оценки нулей. Рассмотрим нуль в клетке (1,2) приведенной матрицы. Он означает, что цена перехода из города 1 в город 2 равна 0. А если мы не пойдем из города 1 в город 2? Тогда все равно нужно въехать в город 2 за цены, указанные во втором столбце; дешевле всего за 1 (из города 6). Далее, все равно надо будет выехать из города 1 за цену, указанную в первой строке; дешевле всего в город 3 за 0. Суммируя эти два минимума, имеем 1+0=1: если не ехать “по нулю” из города 1 в город 2, то надо заплатить не меньше 1. Это и есть оценка нуля. Оценки всех нулей поставлены на табл. 5 правее и выше нуля (оценки нуля, равные нулю, не ставились).

         Выберем максимальную из этих оценок (в примере есть несколько оценок, равных единице, выберем первую из них, в клетке (1,2)).

         Итак, выбрано нулевое ребро (1,2). Разобьем все туры на два класса – включающие ребро (1,2) и не включающие ребро (1,2). Про второй класс можно сказать, что придется приплатить еще 1, так что туры этого класса стоят 35 или больше.

         Что касается первого класса, то в нем надо рассмотреть матрицу на табл. 6 с вычеркнутой первой строкой и вторым столбцом.

1

2

3

4

5

6

1

-

01

0

3

3

6

2

01

-

1

4

1

0

3

1

2

-

01

0

3

4

4

5

01

-

1

3

5

4

2

0

1

-

0

6

7

1

3

3

01

-

табл. 5

1

3

4

5

6

2

01

1

4

1

0

3

1

-

01

0

3

4

4

01

-

1

3

5

4

0

1

-

0

6

7

3

3

01

-

табл. 6

1

3

4

5

6

2

01

1

4

1

0

3

03

-

01

0

3

4

3

01

-

1

3

5

3

0

1

-

0

6

6

3

3

01

-

табл. 7

3

4

5

6

2

1

4

1

0

4

01

-

1

3

5

0

1

-

0

6

3

3

01

-

табл. 8

Дополнительно в уменьшенной матрице поставлен запрет в клетке (2,1), т. к. выбрано ребро (1,2) и замыкать преждевременно тур ребром (2,1) нельзя. Уменьшенную матрицу можно привести на 1 по первому столбцу, так что каждый тур, ей отвечающий, стоит не меньше 35. Результат наших ветвлений и получения оценок показан на рис.6.

Кружки представляют классы: верхний кружок – класс всех туров; нижний левый – класс всех туров, включающих ребро (1,2); нижний правый – класс всех туров, не включающих ребро (1,2). Числа над кружками – оценки снизу.

3

4

6

2

1

3

03

4

03

-

3

5

0

03

0

табл. 10

         Продолжим ветвление в положительную сторону: влево - вниз. Для этого оценим нули в уменьшенной матрице C[1,2] на табл. 7. Максимальная оценка в клетке (3,1) равна 3. Таким образом, оценка для правой нижней вершины на рис. 7 есть 35+3=38. Для оценки левой нижней вершины на рис. 7 нужно вычеркнуть из матрицы C[1,2] еще строку 3 и столбец 1, получив матрицу C[(1,2),(3,1)] на табл. 8. В эту матрицу нужно поставить запрет в клетку (2,3), так как уже построен фрагмент тура из ребер (1,2) и (3,1), т.е. [3,1,2], и нужно запретить преждевременное замыкание (2,3). Эта матрица приводится по столбцу на 1 (табл. 9), таким образом, каждый тур соответствующего класса (т.е. тур, содержащий ребра (1,2) и (3,1)) стоит 36 и более.

3

4

5

6

2

1

3

1

0

4

01

-

1

3

5

0

02

-

0

6

3

2

03

-

табл. 9

3

4

4

0

-

5

0

0

табл. 11

Оцениваем теперь нули в приведенной матрице C[(1,2),(3,1)] нуль с максимальной оценкой 3 находится в клетке (6,5). Отрицательный вариант имеет оценку 38+3=41. Для получения оценки положительного варианта убираем строчку 6 и столбец 5, ставим запрет в клетку (5,6), см. табл. 10. Эта матрица неприводима. Следовательно, оценка положительного варианта не увеличивается (рис.8).

         Оценивая нули в матрице на табл. 10, получаем ветвление по выбору ребра (2,6), отрицательный вариант получает оценку 36+3=39, а для получения оценки положительного варианта вычеркиваем вторую строку и шестой столбец, получая матрицу на табл. 11.

         В матрицу надо добавить запрет в клетку (5,3), ибо уже построен фрагмент тура [3,1,2,6,5] и надо запретить преждевременный возврат (5,3). Теперь, когда осталась матрица 2х2 с запретами по диагонали, достраиваем тур ребрами (4,3) и (5,4). Мы не зря ветвились, по положительным вариантам. Сейчас получен тур: 1→2→6→5→4→3→1 стоимостью в 36. При достижении низа по дереву перебора класс туров сузился до одного тура, а оценка снизу превратилась в точную стоимость.

         Итак, все классы, имеющие оценку 36 и выше, лучшего тура не содержат. Поэтому соответствующие вершины вычеркиваются. Вычеркиваются также вершины, оба потомка которой вычеркнуты. Мы колоссально сократили полный перебор. Осталось проверить, не содержит ли лучшего тура класс, соответствующий матрице С[Not(1,2)], т.е. приведенной матрице С с запретом в клетке 1,2, приведенной на 1 по столбцу (что дало оценку 34+1=35). Оценка нулей дает 3 для нуля в клетке (1,3), так что оценка отрицательного варианта 35+3 превосходит стоимость уже полученного тура 36 и отрицательный вариант отсекается.

         Для получения оценки положительного варианта исключаем из матрицы первую строку и третий столбец, ставим запрет (3,1) и получаем матрицу. Эта матрица приводится по четвертой строке на 1, оценка класса достигает 36 и кружок зачеркивается. Поскольку у вершины “все” убиты оба потомка, она убивается тоже. Вершин не осталось, перебор окончен. Мы получили тот же минимальный тур, который показан подчеркиванием на табл. 2.

         Удовлетворительных теоретических оценок быстродействия алгоритма Литтла и родственных алгоритмов нет, но практика показывает, что на современных ЭВМ они часто позволяют решить ЗК с n = 100. Это огромный прогресс по сравнению с полным перебором. Кроме того, алгоритмы типа ветвей и границ являются, если нет возможности доводить их до конца, эффективными эвристическими процедурами.

1

2

3

4

5

6

7

8

min bk=12

a

1

0

1

0

0

0

0

0

b

12

25

0

18

∞

∞

∞

∞

c

3

3

0

3

3

3

3

3

min bk=18

a

1

0

1

1

0

0

0

0

b

12

25

0

18

∞

38

∞

∞

c

3

3

0

3

3

4

3

3

min bk=25

a

1

1

1

1

0

0

0

0

b

12

25

0

18

47

38

∞

60

c

3

3

0

3

2

4

3

2

min bk=38

a

1

1

1

1

0

1

0

0

b

12

25

0

18

47

38

62

60

c

3

3

0

3

2

4

6

2

min bk=47

a

1

1

1

1

1

1

0

0

b

12

25

0

18

47

38

61

60

c

3

3

0

3

2

4

5

2

min bk=60

a

1

1

1

1

1

1

0

1

b

12

25

0

18

47

38

61

60

c

3

3

0

3

2

4

5

2

Таким образом, для решения ЗК нужно n раз применить алгоритм Дейкстры следующим образом.

         Возьмём произвольную пару вершин

j,k. Исключим непосредственное ребро C[j,k]. С помощью алгоритма Дейкстры найдём кратчайшее расстояние между городами j..k. Пусть это расстояние включает некоторый город m. Имеем часть тура j,m,k. Теперь для каждой пары соседних городов (в данном примере – для j,m и m,k) удалим соответственное ребро и найдём кратчайшее расстояние. При этом в кратчайшее расстояние не должен входить уже использованный город.

Далее аналогично находим кратчайшее расстояние между парами вершин алгоритмом Дейкстры, до тех пор, пока все вершины не будут задействованы. Соединим последнюю вершину с первой и получим тур. Чаще всего это последнее ребро оказывается очень большим, и тур получается с погрешностью, однако алгоритм Дейкстры можно отнести к приближённым алгоритмам.

                                                                                                                                                                                                                                                                                                                                                                                        

III. Выводы

1.Изучены эвристический, приближенный и точный алгоритмы решения ЗК. Точные алгоритмы решения ЗК – это полный перебор или усовершенствованный перебор. Оба они, особенно первый, не эффективны при большом числе вершин графа.

2.Проведён анализ наиболее рациональных методов решения ЗК и определены области их эффективного действия: для малого числа вершин можно использовать точный метод лексического перебора;для большого числа вершин рациональнее применять метод ветвей и границ.

3.Изучены практические применения ЗК и задачи с переналадками, сводимые к ЗК.

4.Приведены тексты программ, позволяющие решить ЗК различными методами.


Литература

1.О. ОреГрафы и их применение. Пер. с англ. под ред. И.М. Яглома. - М., “Мир”, 1965, 174 с.

2.В. П. Сигорский. Математический аппарат инженера. - К., “Техніка”, 1975, 768 с.

3.Ю. Н. Кузнецов, В. И. Кузубов, А. Б. Волощенко. Математическое программирование: учебное пособие. 2-е изд. перераб. и доп. - М.; Высшая школа, 1980, 300 с., ил.

4.Е. В. Маркова, А. Н. Лисенков. Комбинаторные планы в задачах многофакторного эксперимента. – М., Наука, 1979, 345 с.

5.Е. П. Липатов. Теория графов и её применения. - М., Знание, 1986, 32 с.

6.В. М. Бондарев, В. И. Рублинецкий, Е. Г. Качко. Основы программирования. – Харьков, Фолио; Ростов на Дону, Феникс, 1998, 368 с.

7.Ф. А. Новиков Дискретная математика для программистов. - Санкт-Петербург, Питер, 2001, 304 с., ил.