Вынужденные колебания. Амплитудно-частотные и фазово-частотные характеристики
| Загрузить архив: | |
| Файл: ref-20103.zip (210kb [zip], Скачиваний: 195) скачать |
Белорусский государственный университет
Факультет радиофизики и электроники
Реферат
«Вынужденные колебания. Амплитудно-частотные и фазово-частотные характеристики»
Реферат подготовил
студент I курса группы №7
Константин Мулярчик.
Преподаватель:
Янукович Татьяна Петровна.
Минск
2004
Колебания – такие процессы, при которых параметры, характеризующие состояние колебательной системы, повторяются с течением времени. Например, колебания маятника в маятниковых часах, суточные колебания освещённости данного участка Земной поверхности и т.д.
Вынужденные колебания - колебания
системы, возникающие под воздействием внешней вынуждающей силы. Характер этих
колебаний определяется как свойствами самой колебательной системы, так и
внешней силой. Обычно принимают, что внешняя периодическая сила изменяется по
гармоническому закону 
|
|
|
Рис. 1 Система с вынужденными колебаниями |
|
|
|
Рис. 2 Силы, действующие в системе |
Рассмотрим колебательную систему, показанную на рисунке 1.
Она состоит из горизонтального пружинного маятника и кривошипо-шатунного механизма. Кривошипо-шатунный механизм - механизм, который преобразует вращательное движение в возвратно-поступательное.
Тогда II-й закон Ньютона для данной системы запишется в виде:
|
|
(1) |
где  - масса тела,
- масса тела,  – его ускорение,
– его ускорение,  - сила тяжести,
- сила тяжести,  - сила реакции опоры,
- сила реакции опоры,  - сила вязкого трения
(
- сила вязкого трения
(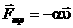
 - внешняя вынуждающая
сила,
- внешняя вынуждающая
сила, 

В проекции на ось x:
|
|
(2) |
введём
замены: 

|
|
(3) |
Введём обозначения  (
( – показатель затухания,
– показатель затухания,
 - коэффициент сопротивления),
- коэффициент сопротивления),
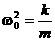 (
( – циклическая частота
свободных колебаний системы в отсутствие трения),
– циклическая частота
свободных колебаний системы в отсутствие трения),  – приведённая сила. Тогда
можем переписать уравнение в общем виде:
– приведённая сила. Тогда
можем переписать уравнение в общем виде:
|
|
(4) |
Уравнение (4) – дифференциальное уравнение вынужденных колебаний, линейное, второй степени, неоднородное (с правой частью). Исследуем его. Как известно из теории дифференциальных уравнений, решением уравнения (4) является сумма двух решений: общего решения однородного уравнения соответствующего данному неоднородному и частного решение неоднородного уравнения в целом.
Однородное уравнение соответствующее данному неоднородному есть уравнение затухающих колебаний
1.
2.
3.
4. :
a.
|
|
(5) |
Решением этого уравнения является функция:
|
|
(6) |
Частное решение неоднородного
уравнения в целом будем искать следующим образом. Как показывает практика, не
зависимо от начальных условий осциллятора через достаточно большой промежуток
времени (время разгорания/релаксации) в системе установятся гармонические колебания
с частотой вынуждающей силы  и амплитудой
и амплитудой 

|
Различные случаи установления гармонических колебаний: |
|
|
|
|
|
Рис. 3 Случай разгорания для |
Рис. 4 Произвольный случай разгорания |
Здесь 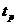 – этовремя разгорания колебаний.
– этовремя разгорания колебаний.
Это значит, что через достаточно
большой промежуток времени первым слагаемым можно пренебречь. Действительно в
(6) при 

|
|
(7) |
где
 - амплитуда
установившихся колебаний с частотой
- амплитуда
установившихся колебаний с частотой 
 - сдвиг фаз между
смещением и фазой внешней силы.
- сдвиг фаз между
смещением и фазой внешней силы.
Найдем, чему равны  и
и  при частоте внешней
силы
при частоте внешней
силы 
|
|
(8) |
|
|
(9) |
И подставим (7), (8), (9) в (4):

немного преобразуем:

и получим:


 и
и  будут равны нулю:
будут равны нулю:

Из этой системы найдем зависимость амплитуды установившихся колебаний и сдвига фаз от частоты внешней вынуждающей силы:
|
|
(10) |
|
|
(11) |
Исследуем выражение
(11) на экстремумы. Очевидно, что
амплитуда колебаний будет максимальной в том случае, если подкоренное выражение
в (11) будет минимальным. Обозначим 

Таким образом, подкоренное выражение (и, соответственно, амплитуда колебаний) принимает экстремальное значение при:
|
|
(12) |
|
|
(13) |
Если производная  амплитуда – максимальной. Вторая производная
от подкоренного выражения равна:
амплитуда – максимальной. Вторая производная
от подкоренного выражения равна:

Значение этой
производной при  равно
равно  а при
а при 



Явление резкого увеличения амплитуды вынужденных колебаний при определённой частоте вынуждающей силы называется резонансом.
Таким образом, резонансная частота равна
|
|
(14) |
Учитывая это значение, по (10) и (11) находим резонансные значения сдвига фаз и амплитуды колебаний:
|
|
(15) |
|
|
(16) |
Из (15) и (16) видно, что при отсутствии трения
(

Для вынужденных
колебаний вводят, так называемые, амплитудо-частотные
(зависимость амплитуды колебаний от частоты вынуждающей силы) и фазово-частотные (зависимость сдвига
фаз от частоты вынуждающей силы) характеристики. Графически эти зависимости
при различных значениях  приведены на рисунках
5 и 6:
приведены на рисунках
5 и 6:
|
|
|
|
Рис.5 Амплитудно-частотные характеристики |
Рис.6 Фазово-частотные характеристики |
Отметим
здесь, что в отсутствие трения изменение фазы вынужденных колебаний на величину
 происходит скачком при
происходит скачком при

При установившемся движении, когда система совершает вынужденные колебания по закону (), ее энергия, очевидно, остается неизменной. Однако при этом внешняя сила непрерывно совершает работу над системой. Иными словами, система непрерывно поглощает (от источника внешней силы) энергию, которая, в конечном счете, диссипируется в тепло благодаря наличию трения.
Пусть  обозначает количество энергии,
поглощаемой системой в среднем в единицу времени, как функция частоты
вынуждающей силы. Эта величина, как известно, равна работе внешней силы за
единицу времени, то есть мощности (усредненной затем по времени):
обозначает количество энергии,
поглощаемой системой в среднем в единицу времени, как функция частоты
вынуждающей силы. Эта величина, как известно, равна работе внешней силы за
единицу времени, то есть мощности (усредненной затем по времени):
|
|
(17) |
Отсюда, согласно уравнению движения,
|
|
(18) |
Здесь,
в (17) и (18), символ  обозначает работу.
обозначает работу.
При усреднении по времени первое и третье слагаемые в этом выражении, будучи произведениями синуса на косинус, очевидно, дают нуль. В результате остается лишь вклад от второго слагаемого
|
|
(19) |
Подставляя сюда (8), получаем:
|
|
(20) |
Производя усреднение по времени, заметим, что второе слагаемое зануляется, поэтому:
|
|
(21) |
Подставляя сюда (11), получим:
|
|
(22) |
Исследуем это выражение на
экстремумы. Очевидно, что экстремальное значение оно примет при экстремальном
значении знаменателя. Производная от знаменателя обращается в нуль при 
Вблизи резонанса  амплитуда
амплитуда  определяется формулой
(16). Введём величину
определяется формулой
(16). Введём величину 


Таким образом:
|
|
(23) |
Такой вид зависимости поглощения от
частотной расстройки относительно резонанса называют дисперсионным. Полушириной
резонансной кривой (см. рис. 7)  называется значение
называется значение 
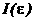 уменьшается вдвое по сравнению
с ее максимальным значением при
уменьшается вдвое по сравнению
с ее максимальным значением при 

Рис. 7 Резонансная кивая поглощения
Из формулы (23) следует, что в pассматpиваемом
случае 
|
|
(24) |
обратно
пpопоpциональна 
 резонансная кривая
становится уже и выше, то есть ее максимум становится более острым. Однако площадь
под резонансной кривой остается при этом неизменной.
резонансная кривая
становится уже и выше, то есть ее максимум становится более острым. Однако площадь
под резонансной кривой остается при этом неизменной.
Линейность уравнений движения, описывающих вынужденные гармонические колебания (с трением и без него), приводит к тому, что оказывается справедливым, так называемый, принцип суперпозиции колебаний.
Пусть, например, на систему, совершающую колебательное движение, действует внешняя сила, зависящая от времени и представляющая собой суперпозицию двух сил
|
|
(25) |
Это
могут быть, напpимеp, периодические по времени функции с различными частотами  и
и 
|
|
(26) |
Согласно принципу суперпозиции, решение этого уравнения есть сумма решений того же уравнения под воздействием каждой из сил в отдельности, то есть
|
|
(27) |
где
функции  и
и  удовлетворяют уравнениям
удовлетворяют уравнениям
|
|
(28) |
Проверяется это утверждение непосредственной
подстановкой. Для
этого первое из уравнений (28) складывают со вторым. В силу линейности всех операций
в левой части уравнения (28), мы и приходим к сформулированному выше принципу суперпозиции
колебаний.
Список использованных материалов:
- И.В. Савельев «Курс общей физики» Том I. Механика
- С.П. Стрелков «Механика»
- Д.В. Сивухин «Общий курс физики» Том I. Механика
- Сайт «Научно-образовательный Центр ФТИ им.А.Ф.Иоффе» ()



































