Исследование кривых и поверхностей второго порядка


	Загрузить архив:
	Файл: ref-21604.zip (127kb [zip], Скачиваний: 370) скачать

Международныйуниверситет природы, общества и человека

«Дубна»

Кафедра высшей математики

Курсовая работа

по линейной алгебре и аналитической геометрии

студентки I курса 1033 группы

Ярмак Елены Владимировны

«Исследование кривых и поверхностей

второго порядка»

Руководители: старший преподаватель Маркова И. А.

ассистент Павлов А. С.

Дубна, 2002

Оглавление. PAGEREF _Toc28246427 h 2

Задание 1. PAGEREF _Toc28246428 h 3

Задание 2. PAGEREF _Toc28246429 h 3

Цель. PAGEREF _Toc28246430 h 3

Задача. PAGEREF _Toc28246431 h 3

Исходные данные. PAGEREF _Toc28246432 h 4

Анализ кривой второго порядка. PAGEREF _Toc28246433 h 4

1. Определение зависимости типа данной кривой (1) от параметра b с помощью инвариантов PAGEREF _Toc28246434 h 4

2. Приведение уравнения кривой при b = 0 к каноническому виду, применяя преобразования параллельного переноса и поворота координатных осей. PAGEREF _Toc28246435 h 6

4. Вывод уравнения осей канонической системы координат.. PAGEREF _Toc28246436 h 8

5. Построение кривой в канонической и общей системах координат.. PAGEREF _Toc28246437 h 9

Анализ поверхности второго порядка. PAGEREF _Toc28246439 h 11

1. Исследование формы поверхности методом сечений и построение полученных сечений PAGEREF _Toc28246440 h 11

2. Построение поверхности в канонической системе координат.. PAGEREF _Toc28246441 h 16

Вывод. PAGEREF _Toc28246442 h 17

Список использованной литературы.. PAGEREF _Toc28246443 h 18

Задание 1

1.Определить зависимость типа данной кривой от параметра b с помощью инвариантов.

2. Привести уравнение кривой при b = 0 к каноническому виду, применяя преобразования параллельного переноса и поворота координатных осей.

3. Найти фокусы, директрисы, эксцентриситет и асимптоты (если они есть) данной кривой второго порядка.

4. Написать уравнения осей канонической системы координат.

5. Построить кривую в канонической и общей системах координат.

Задание 2

Для данного уравнения поверхности второго порядка:

1. Исследовать форму поверхности методом сечений и построить полученные сечения.

2. Построить поверхность в канонической системе координат.

Цель

Целью курсовой работы является закрепление и углубление полученных студентом знаний и технических навыков по изучению и анализу свойств кривых и поверхностей второго порядка.

Определить зависимость типа данной кривой от параметра b с помощью инвариантов. Привести уравнение кривой при b = 0 к каноническому виду, применяя преобразования параллельного переноса и поворота координатных осей. Найти фокусы, директрисы, эксцентриситет и асимптоты (если они есть) данной кривой второго порядка. Написать уравнения осей канонической системы координат. Построить кривую в канонической и общей системах координат.

Исследовать форму данной поверхности методом сечений и построить полученные сечения. Построить поверхность в канонической системе координат.

Исходные данные

Уравнение кривой второго порядка:

Уравнение поверхности второго порядка:

Их инварианты и классификация.

Анализ кривой второго порядка

Для данного уравнения кривой второго порядка:

(1)

1. Определение зависимости типа данной кривой (1) от параметра b с помощью инвариантов

Для уравнения кривой второго порядка (1) имеем:

Вычислим инварианты кривой

В соответствии с классификацией кривых второго порядка:

Если I₂ = 0, то уравнение (1) определяет кривую параболического типа. Но
I₂= -306-11b , следовательно, если

Если I₂ ¹ 0, то данная кривая – центральная. Следовательно, при данная кривая – центральная.

Если I₂ > 0, то уравнение (1) определяет кривую эллиптического типа. Следовательно, если I₁I₃= (1-b)(4885b-306) < 0, и в соответствии с признаками кривых второго порядка (I₂ > 0, I₁I₃ < 0) получим, что если

Если I₂ < 0, то уравнение (1) определяет кривую гиперболического типа. Следовательно, если

Если I₂ < 0 и I₃ = 0, то уравнение (1) определяет две пересекающиеся прямые. Получим:

Следовательно, если

Если I₂ < 0 и I₃ ¹ 0, то данная кривая – гипербола. Но I₃ ¹ 0 при всех за исключением точки

Значение параметра b
Тип кривой	Эллипс	Парабола	Гипербола	Две пересекающиеся прямые	Гипербола

2. Приведение уравнения кривой при b = 0 к каноническому виду, применяя преобразования параллельного переноса и поворота координатных осей

При b = 0 уравнение (1) принимает следующий вид:

(2)

Согласно таблице, это гипербола. Приведем уравнение кривой (2) к каноническому виду, применяя преобразования параллельного переноса и поворота координатных осей.
Мы установили, что данная кривая – центральная, поэтому используем методику приведения к каноническому виду для уравнения центральной кривой.

а) Совершим параллельный перенос начала координат в точку x, y произвольной точки М плоскости в системе координат xOy и координаты x’, y’ в новой системе координат x’O’y’ связаны соотношениями:

Подставляя эти выражения для x и y в уравнение (1), получим:

Раскрывая скобки и приводя подобные члены, получим уравнение вида

В этом уравнении коэффициенты при x’ и y’ приравняем к нулю. Получим систему уравнений относительно

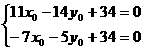
которая определяет координаты центра исходной кривой. Следовательно, - решение данной системы и точка О’(2, 4) – центр данной кривой. Подставим найденные значенияв уравнение (2), получим

(3)

б) Дальнейшее упрощение уравнения (3) достигается при помощи поворота осей координат на угол a.

При повороте осей координат на угол a координаты x’, y’ произвольной точки М плоскости в системе координат х’O’y’и координаты Х, Y в новой системе координат XO’Y связаны соотношениями:

(4)

Подставляя (4) в уравнение кривой (3), получим:

Раскроем скобки и приведем подобные члены, получим уравнение вида:

(5)

Выберем угол a такой, что в уравнении (5) коэффициент при произведении X×Y равен нулю:

Это требование эквивалентно уравнению:

(6)

Решая уравнение (6), получим:

Tga=k, k – угловой коэффициент оси О’Х. Он определяется формулой:

l₁ – корень характеристического уравненияданной кривой, совпадающий со знаком I₃. Характеристическое уравнение для данной кривой (1) имеет вид

Следовательно,

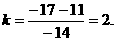
Тогда получим, что tga найдем sina и cosa:

Подставляя эти значения в уравнение (5), получим:

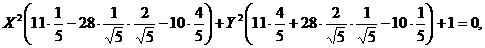
т. е. преобразование уравнения будет иметь вид

и, соответственно, уравнение

- это каноническое уравнение исходной гиперболы с центром в точке O’(2, 4) и полуосями и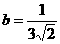

3. Нахождение фокусов, директрис, эксцентриситета и асимптот (если они есть) данной кривой второго порядка

Найдем фокусы гиперболы. Коoрдинаты F_1,2 равны (±с, 0), с определяется по формуле:

Следовательно, точки и - фокусы данной гиперболы.

Найдем эксцентриситет гиперболы:

Найдем директрисы гиперболы:

D₁: D₂: .

Найдем асимптоты гиперболы:

4. Вывод уравнения осей канонической системы координат

Напишем уравнения осей канонической системы координат. Из задания 2 известно, что точка О’(2, 4) – центр данной кривой. Оттуда же известен угловой коэффициент оси O’X XO’Y в исходной системе координат xOy. Так как система XO’Y– каноническая для данной гиперболы, то ее центр находится в центре кривой – точке О’(2, 4), т е. оси О’X и O’Y проходят через точку О’. Уравнение прямой, проходящей через данную точку k имеет вид:
Следовательно, ось О’X в системе координат xOy имеет уравнение

Так как ось О’Y перпендикулярна оси О’X, то ее угловой коэффициент Следовательно, ось О’Y имеет уравнение или

5. Построение кривой в канонической и общей системах координат

На основе полученной информации, нарисуем кривую в канонической и общей системах координат:

Рис. 1. Кривая в общей и канонической системах координат.

Рис. 2. Кривая в канонической системе координат.

Анализ поверхности второго порядка

Для данного уравнения поверхности второго порядка:

(7)

1. Исследование формы поверхности методом сечений и построение полученных сечений

1) Для того чтобы исследовать поверхность методом сечений, сначала приведем уравнение (7) к каноническому виду с помощью параллельного переноса и поворота осей координат.

Совершим параллельный перенос начала координат в точку x, y, zпроизвольной точки М плоскости в системе координат Oxyz и координаты x’, y’, z’ в новой системе координат O’x’y’z’ связаны соотношениями:

Подставляя эти выражения для x, y, z в уравнение (7), получим:

Раскрывая скобки и приводя подобные члены, получим уравнение вида

(8)

В уравнении (8) коэффициенты при x,’ y’, z’ приравняем к нулю. Получим систему уравнений относительно ,

которая определяет координаты центра исходной поверхности. Следовательно, - решение данной системы и точка – центр данной поверхности. Подставим найденные значения , в уравнение (8), получим

(9)

Дальнейшее упрощение уравнения (3) достигается при помощи поворота осей координат на угол a. При повороте осей координат O’Yи O’Zна угол a координаты y’, z’ произвольной точки М плоскости yOzв системе координат O’х’y’z’ и координаты Y, Zв новой системе координат O’XYZ связаны соотношениями:

(10)

Подставляя (10) в уравнение поверхности (9) с последующим раскрытием скобок и приведением подобных членов, получим уравнение вида:

(11)

Выберем угол a такой, что в уравнении (11) коэффициент при произведении Y×Z равен нулю:

Получим, что 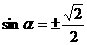a, решим характеристическое уравнение для эллипса

Отсюда вычислим угловой коэффициент поворота осей k:

Следовательно, cosa= sina = ±

Подставляя эти значения в уравнение (11), получим:

т. е. уравнение

(12)

– это каноническое уравнение для данной поверхности, которое задает эллипсоид с полуосями и a=b, то эллипсоид называется сплюснутым.

2) Данное каноническое уравнение (12) задает эллипсоид.

Рассмотрим линии, полученные в сечениях эллипсоида плоскостями Z=h (h=const). Эти линии определяются системой уравнений:

Решая эту систему, получаем:

(13)

где h – любое вещественное число. Уравнения (13) – это уравнения окружностей с радиусом ½h½, с центрами на оси O’Zв точках C(0, 0, h). Плоскость XO’Y(h=0) пересекает эллипсоид по окружности:

Эта окружность будет наибольшей, как видно из выражения радиуса. При получаем уравнение:

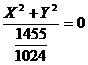
т. е. сечения в таких значениях h будут представлять собой точки в центре координат полученных сечений. При получаем отрицательное число под корнем, т. е. при таких значениях h плоскость XO’Yне пересекает данный эллипсоид. При получаем окружность:

Изобразим полученные сечен

Рис. 3. Сечение плоскостью Z=h.

Рассмотрим линии, полученные в сечениях эллипсоида плоскостью X=h:

Решая эту систему, получаем:

(14)

где h – любое вещественное число. Уравнения (14) – это уравнения эллипсов с полуосями:

уменьшающимися с увеличением ½h½, с центрами на оси O’Xв точках C(h, 0, 0) и осями, параллельными плоскости YO’Z.

Плоскость YO’Z(h=0) пересекает эллипсоид по эллипсу

Этот эллипс будет наибольшим, как видно из выражения полуосей. При получаем уравнение

т. е. сечения в таких значениях h будут представлять собой точки в центре координат полученных сечений. При получаем

т. е. при таких значениях h плоскость YO’Zне пересекает данный эллипсоид. При получаем эллипс:

Изобразим полученные сечения:

Рис. 4. Сечение плоскостью X=h.

Аналогичная картина получаются при сечении эллипсоида плоскостью XO’Z.

Преподаватель.	Оценка.	Подпись.	Дата.