Шпаргалка (математика)

Сдавался/использовался	Июнь/2005г.
	Загрузить архив:
	Файл: ref-21978.zip (64kb [zip], Скачиваний: 111) скачать

№1

lim (∆x→0) ∆f/∆x = f’(x)

∆f/∆x = f’(x)+α(∆x), где

lim (∆x→0) α(∆x)=0

∆f = f’(x)∙∆x+ α(∆x)∙∆x

Опред-е: диф-ом к ф-ии наз-ся вел-на пропорциональная приращ-ю аргумента и отлич-ся от приращ-я ф-ии на вел-ну беск. малую по сравнению с прир-м аргумента.

df(x)=k∙∆x

∆f-df(x)=0(∆x)

∆f=df(x)+ 0(∆x)

Теорема: д/того, чтобы у ф-ии f(x) сущ-ал дифф-л, необх. и достаточно, чтобы ф-ия была диф-ма в эт. (∙), т.е. чтобы у нее сущ-ла производная в эт. (∙).

df(x)= f’(x) ∙∆x

y=x

dx=∆x

df(x)= f’(x)dx

№2

Св-ва диф-а:

1) dc=0

2) d(cf(x))=cdf(x)

3) d(ax+b)=ad(x), где a и b-пост. величины

4) d(u ± v)= du ± dv

5) d(uv)=udv+vdu

6) d(u/v)=( vdu-udv)/v²

7) df(u(x))=f’_u(u)du

8) dφ(u)= φ’(u)du

№3

Будем предполагать, что приращение независ. переменной произвольно и не зависит от конкрет. Знач-я арг. Х и одно и то же д/всех значений этого аргумента.

df(x)=f’(x)dx

d(df(x))=d²f(x)=d(f’(x)dx)=dx∙d(f’(x))=dxf”(x)dx=f”(x)∙dx²

d²f(x)/ dx²= f”(x)

dⁿf(x)=f⁽ⁿ⁾(x)dxⁿ – диф. n-го порядка f(x)

f(x)=x

dx=∆x

dx²=0

dxⁿ=0

Теорема: диф-ы высшего порядка д/независ. перемен. = 0.

№4

Опред-е: первообразной д/ф-ии f(x) наз-ся ф-ия F(x), такая, что F’(x)= f(x).

(F(x)+С)’= F’(x)+ С’= f(x)

Опред-е: совокупность всех первообразных д/ф-ии f(x) наз-ся неопред. ∫ от ф-ии f(x) и обознач.: ∫ f(x)dx = F(x)+С, где d-диф-л, f(x)-подинтегр. ф-ия, f(x)dx-подинтегр. выр-е.

Св-ва:

1) (∫f(x)dx)’=f(x)

2) d ∫f(x)dx= f(x)dx (диф-л от неопред. ∫=подинт. выр-ю)

3) ∫dφ(x)=φ(x)+C (∫ от диф-ла люб. ф-ии = этой ф-ии с точностью до пост. слагаемого)

4) ∫af(x)dx=a∫f(x)dx

5) ∫[f(x) ± g(x)]dx = ∫f(x)dx ± ∫g(x)dx

№5

∫f(φ(x))φ’(x)dx = ∫f(φ(x))dφ(x) = ∫f(u)du

u= φ(x)

Пример:

∫dx/2x+3 = ∫(dt/2)/t = 1/2∫dt/t = ½ ln|t|+C = ½ ln|2x+3|+C

2x+3=t

2dx=dt

dx=dt/2

№6

d(uv)=udv+vdu

∫d(uv)= ∫udv + ∫vdu

uv = ∫udv + ∫vdu

∫udv = uv - ∫vdu

Пример:

∫xsinxdx = -xcosx+∫cosxdx = -xcosx+sinx+C

u=x

dv=sinxdx

du=dx

v=∫sinxdx=-cosx

№7

f(x) [a, b]

n – произв. Целое положит. Число

Выберем (∙)-и t₀ = a12<…n = b

{ t₀; t₁; t₂;… t_n} = T_n – совокуп. точек – разбиение отрезка [a, b].

[t_i; t_i-1]

∆_i = t_i - t_i-1 – длина i-подотрезка

Ф-ия, опред-я на отрез. [a, b].

∆=max {∆₁, ∆₂, …∆_n}

Выберем произв. внутр. (∙) t_i-1≤ ε_i ≤ t_i

Σⁿ_i=1f(ε_i)∆_i = f(ε₁)∆₁+ f(ε₂)∆₂+…+ f(ε_n)∆_n – это интегр-я сумма д/ф-ии f(t) соотв-й разбиению Т_n и набору (∙)-ек ε₁ и т.д. ε_n.

Σⁿ_i=1f(ε_i)∆_i = I(f(t), Т_n, ε₁…ε_n)

Опред-е: если сущ-т конеч. предел послед-ти интегр-х сумм при усл-ии, что ∆→0 и этот lim не зависит от выбора разбиений Т_n и выбора промеж. (∙)-ек ε₁ и т.д. ε_n, то ф-ия f(t) наз-ся интегр-й на отрез. [a, b], а этот lim наз-ся опред. ∫ от ф-ии f(t) по отрезку [a, b] и обознач-ся: _a∫^bf(t)dt = lim(∆→0) I(f(t), Т_n, ε₁…ε_n), где a – ниж. предел интегр-я,b – верх. предел интегр-я, f(t) – подинт. ф-ия, f(t)dt – подинт. выр-е.

№8

Д/V ф-ии f(t) _a∫^bf(t)dt =0

1) _a∫^bdt =b-a

2) _a∫^b cf(x)dx = c _a∫^bf(x)dx

3) Если ф-ии f(x) и g(x) интегрируемы на отрез. [a, b], то ф-ия f(x)+g(x) также интегр-ма на отрез. [a, b]. _a∫^b [f(x)+g(x)]dx = _a∫^b f(x)dx + _a∫^b g(x)dx.

4) _a∫^bf(x)dx = - _b∫^af(x)dx – если изменить направ-е интегр-я, то измен-ся и знак.

5) Если ф-ия f(x) интегр-ма на отрез. [a, b] (a

6) Если ф-ия f(x) интегр-ма на отрез. [a, b], а (∙)с лежит внутри отрез. [a, b], то

_a∫^bf(x)dx = _a∫^с f(x)dx + _с∫^bf(x)dx.

7) Если ф-ия f(x) непрерывна на отрез. [a, b], то она интегр-ма на этом отрезке.

8) Если ф-ия f(x) интегр-ма на отрез. [a, b] и ограничена на этом отрезке, то

m(b-a) ≤ _a∫^b f(x)dx ≤ M(b-a); _a∫^b mdx = m _a∫^bdx = m(b-a)

9) Если ф-ии f(x) и g(x) интегрируемы на отрез. [a, b] и во всех (∙)-ах этого отрез. Вып-ся нер-во m(b-a) ≤ _a∫^bf(x)dx ≤ M(b-a), то f(x) не превосходит g(x): f(x) ≤ g(x);

_a∫^bf(x)dx ≤ _a∫^bg(x)dx.

10)Теорема о среднем: если ф-ия f(x) непрерыв. на отрез. [a, b], то сущ-т (∙)с, лежащая внутри этого отрезка или на его границе, такая, что: _a∫^bf(x)dx = f(c)∙(b-a).

№9

Пусть ф-ия f(x) определена и интегр-ма на отрез. [a, b]. Если выбрать нек. произв-е числа a≤c

Ф(х) = _с∫^х f(t)dt.

Св-ва ф-ии Ф(х):

предположим f(x) непрерывна

х+∆х

Ф(х+∆х) – Ф(х) = _с∫^х+∆х f(t)dt - _с∫^х f(t)dt = _х∫^х+∆х f(t)dt = f(с)∙∆х, где (∙)с лежит внутри интерв. (х+∆х).

1) Если ∆х→0, ф-ия непрерыв., т.е. ограничена => опред. ∫ тоже непрерыв.

2) lim (∆х→0) ∆Ф/∆х = f(x)

Т.е. введенная ф-ия Ф(х) – первообраз. д/ф-ии f(x).

№10

Пусть Ф(х) – какая-то первообраз-я д/ф-ии f(x), тогда можно утверждать, что:

_a∫^х f(t)dt = F(x)+C д/люб. х из интерв. [a, b], тогда _a∫^a f(t)dt =0; F(a)+C=0; C=-F(a)

_a∫^b f(t)dt = F(b) – F(a) – формулаЛейбница-Ньютона.

№11

_a∫^b f(х)dх = _α∫^βf(φ(t)) φ’(t)dt

x= φ(t)

x=a => a=φ(t), t = φ^-1(a) = α

x=b => b=φ(t), t = φ^-1(b) = β

dx = φ’(t)dt

№12

Будем предполагать, что ф-ии u и v интегр-мы на отрез. [a, b] и диффер-мы на этом отрез.

d(uv) = udv+vdu; проинтегр-м по отрез. [a, b] это рав-во

_a∫^bd(uv) = _a∫^budv + _a∫^bvdu

u(b)v(b) – u(a)v(a) = _a∫^budv + _a∫^bvdu

_a∫^budv = u(b)v(b) – u(a)v(a) - _a∫^bvdu – правило интегр-я по частям в опред. ∫.

№13

2 случая: 1) ф-ия неогранич. растет в (∙); 2) интегр-ие на беск. интервале.

1) Пусть ф-ия f(х) определена на интерв. (a, b), но limf(x) = ∞, тогда _a∫^bf(х)dх будет наз-ся несобств. интегралом.

Под ним поним-ся lim (ε→0) _a+ε∫^bf(x)dx

_a∫^b f(x)dx = lim (ε→0) _a+ε∫^b f(x)dx.

Если этот предел сущ-т и конечен, то данный ∫ наз-ся сход-ся.

2) Оба, или хотя бы 1 предел интегр. Неограничен.

_a∫^+∞ f(x)dx = lim (А→ +∞) _a ∫^А f(x)dx

Если этот предел сущ-т и конечен, то данный ∫ наз-ся сход-ся.

_-∞∫^bf(x)dx = lim (B→ -∞) _B∫^bf(x)dx

_-∞∫^+∞ f(x)dx = _-∞∫⁰ f(x)dx + ₀∫^+∞f(x)dx – обобщение.

№14

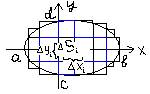
Пусть ф-ия f(x)>0 на отрез. [a, b]

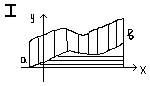
Выберем нек. целое положит. число n и разобьем отрезок[a, b] на n одинак. подотрезков.

(b-a)/n = R

x₀ = a; y₀ = f(x₀)

x₁=a+h; y₁=f(x₁)

--------; ---------

x_i=a+ih

x_n=b=a+nh; y_n=f(x_n)

S_i = (y_i-1 + y_i)/2 ∙h

S=S₁+S₂+…S_n = h∙[(y₀+y_n)/2 + y₁+y₂…+y_n-1]

_a∫^b f(x)dx = h∙[(y₀+y_n)/2 + y₁+y₂…+y_n-1]

№15

y=αx²+βx+γ

y_i-1 = αx²_i-1+βx_i-1+γ = α(x_i-h)²+ β(x_i-h)+ γ

y_i=αx_i²+βx_i+γ; y_i-1 = αx_i²- 2αhx_i + 2h² +βx_i – βh +γ

y_i+1 = α(x_i+h)²+ β(x_i-h)+ γ; y_i+1 = αx²_i +2αhx_i +2h² + βx_i + βh +γ

y_i+1+ y_i-1 = 2 αx²_i + 2αh² + 2βx_i + 2γ

y_i+1+ y_i-1 = 2y_i = 2αh²

α = (y_i+1+ y_i-1 – 2y_i)/ 2h²

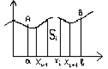
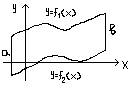
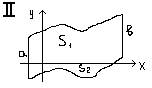
S_i = _xi-1∫^xi+1(αx²+βx+γ)dx = (αx³/3 + βx²/2 + γx) | ^xi+1_xi-1 = α∙[(x_i+h)³ – (x_i-h)³]/3 + β∙[(x_i+h)² – (x_i-h)²]/2 + γ∙[(x_i+h) – (x_i-h)]/1 = α/3∙(6x²_ih + 2h³) + β/2∙(4x_ih) + 2γh = (2hαx_i² + 2hβx_i + 2hγ) + 2/3∙h³α = 2hy_i + 2/3∙h³∙( y_i+1+ y_i-1– 2y_i)/ 2h² = h∙(6y_i + y_i+1+ y_i-1- 2y_i)/3

S_i= ( y_i+1+ 4y_i + y_i-1)/3∙h – формула Симпсона

№16

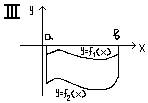
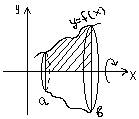
S=_a∫^b (f₁(x) – f₂(x))dx

S₂ = - _a∫^b f₂(x)dx

S = _a∫^b(f₁(x) – f₂(x))dx

№17

y = f(x)

{x=φ(t)

{y=Ψ(t)

α ≤ t ≤ β

cos²φ + sin²φ = 1

{x=a∙cosφ

{y=a∙sinφ

0 ≤ φ ≤ 2π

S = ₀∫^a ydx = ­ - _π/2∫⁰ sin²φdφ = a² ₀∫^π/2 sin²φdφ = a² ₀∫^π/2 (1-cos2φ)/2 dφ = a²π/4

S = _α∫^βy(t)x’(t)dt – вычисление S кривой, если ее Ур-е задано парам-ки.

№18

l – вектор, ρ – длина вектора ОМ

{x = ρcosφ

{y = ρsinφ

ρ = √(x² +y²)

tgφ = y/x

ρ = ρ(φ) – в полярн. сис. коорд.

ρ(φ)    ρ(φ +dφ)

ds = ρ²/2 dφ

_α∫^βds = S = ½ _α∫^βρ²dφ

S = ½ _α∫^βρ²dφ

№19

В дугу АВ вписали ломаную.

M_i (x_i, y_i)

y_i= f(x_i) (если ур-е кривой y = f(x))

| M_i-1M_i | = √[(x_i – x_i-1)² + (y_i – y_i-1)²]

l_лом = Σⁿ_i=1 √[(x_i – x_i-1)² + (y_i – y_i-1)²] – длина ломаной линии.

Опред.: под длиной дуги АВ будем понимать lim длины впис. Ломаной, когда число звеньев неогранич-о растет, а длина max звена стремится к 0.

При оч. мал. ∆х: dl = √[(dx)² + (dy)²] = √[(dx)² +(y’_x)² + (dx)²] =√ [1+(y’_x)²] dx

l_{дуги ab} = _a∫^b√ [1+(y’_x)²] dx – формула д/вычисл. длины дуги.

№20

{x=φ(t)

{y=Ψ(t)

dx = φ’(t)dt

dy = Ψ’(t)dt

l_{дуги ab} = _α∫^β √ [ (φ’(t))² + (Ψ’(t))²] dt

№21

{x = ρcosφ

{y = ρsinφ

dx = (ρ’cosφ – ρsinφ)dφ

dy = (ρ’sinφ + ρcosφ)dφ

(dx)² = (ρ’²cos²φ – 2ρ’ρcosφsinφ + ρ²sin²φ)

(dy)² = (ρ’²sin²φ + 2ρ’ρcosφsinφ + ρ²cos²φ)

dl = √[(ρ’)² + ρ²] dφ

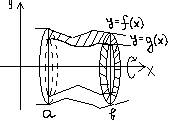
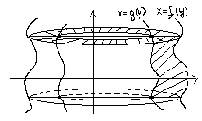
l = _α∫^β √[(ρ’)² + ρ²] dφ

№22

I Вокруг х

a) { y = f(x)

    {x = a, x = b

    {y = 0

V_x = π_a∫^bf²(x)dx

б) Час. случай

V_x = π_a∫^bf²(x)dx - π_a∫^bg²(x)dx = π_a∫^b [f²(x) - g²(x)]dx

II Вокруг y

a)

V_y = π _c∫^d g²(y)dy

б) Час. Случай

V_y = π_c∫^df²(y)dy - π_c∫^dg²(y)dy = π_c∫^d [f²(y) - g²(y)]dy

№23

Опред-е: числ. ряд – сумма беск. числа слаг-ыхu₁+u₂+…+u_n = Σ^∞_n=1u_n(1), каж. из кот. – опред. число.

u_n = n/(n²+1)

Последов-ть частичных сумм:

S₁ = u₁

S₂ = u₁+u₂

S₃ = u₁+u₂+u₃

----------------

S_n = u₁+u₂+…+u_n

Σ^∞_n=1 u_n = S_n + Σ^∞_k=n+1 u_k = S_n + r_n, r_n – n-йостатокряда

Опред-е: ряд 1 наз-ся сход-ся рядом, если у него сущ-т, конечен lim послед-ти частичных сумм, а сам этот lim наз-ся суммой числ. ряда.

S = lim (n→∞) S_n

Опред-е: если у этой послед-ти частич. сумм нет lim или lim=∞, то ряд наз-ся расход-ся.

Теорема: д/того, чтобы ряд 1 сходился, необх-о и достат-о, чтобы остаток ряда → к 0, т.е. чтобы lim (n→∞) r_n = 0

Теорема (необх. усл-е сход. ряда)2: если ряд 1 сход-ся, то lim (n→∞) u_n = 0.

Следствие из теор.2: если n-й член ряда не → к 0, то ряд расх-ся.

№24

Основ. св-ва сход. рядов:

1) Если члены сход-ся ряда умнож. на 1 и то же конеч. число, то нов. получ-й ряд будет тоже сход-ся, и сумма этого нов. ряда будет = произвед. эт. числа на сумму исход. ряда, т.е. Σ^∞_n=1u_n = S; Σ^∞_n=1 λ∙u_n = λ∙S

2) Если ряд 1 сход-ся и к нему добавить конеч. число слаг-х, либо из него убрать конеч. число слаг-х, то получ. нов. ряд будет тоже сход-ся.

3) Если ряд с членами u_n сход-ся и его сумма = Σ^∞_n=1u_n = S и ряд с членами v_n сход-ся и его сумма = Σ^∞_n=1v_n = σ, то ряд с чл. (u_n + v_n) сход-ся и его сумма = Σ^∞_n=1 (u_n + v_n) = S+ σ

Σ^∞_n=11/ n = 1+1/2+1/3+…+1/n… - гармонич. ряд

№25

Признак Даламбера: Пусть дан ряд Σ^∞_n=1u_n, если lim (n→∞) u_n+1/u_n = k

{k<1 – ряд сх.

{k>1 – ряд расх.

{k=1 – вопр. о сход. ряда ост-ся открытым

Интегральный признак: Им-ся ряд с положит. членами. u_n = f(n) – эта ф-ия определена на интерв. [1; +∞]. Если ₁∫^∞ f(x)dx несобств. интеграл сход-ся, то изнач. ряд тоже сход-ся.

Σ^∞_n=11/ n – гарм. ряд; Σ^∞_n=11/ n^α – обобщ. гарм. ряд.

f(x) = 1/x^α

₁∫^∞ dx/x^α = lim (A→∞) ₁∫^Adx/x^α = lim (A→∞) [-αx^-α+1] |^A₁ = lim (A→∞) [α - αA^-α+1] = lim (A→∞) [α – α/A^-α+1]

Если α>1, вычит. → к 0 при А→ ∞, ряд сход-ся.

Если α≤1, А-b положит. степ., при А→ ∞ ряд расх-ся.

№26

Σ^∞_n=1 (-1)ⁿ⁺¹u_n = u₁-u₂+u₃- u₄+…, причем u_n≥0

Теорема Лейбница: если д/членов знакочеред-ся ряда справедливы соотнош-я u_n+1< u_n

и lim (n→∞) u_n = 0, то дан. ряд сход-ся.

Док-во:

Найдем 2n частичную сумму ряда:

S_2n = (u₁–u₂) + (u₃-u₄) +…+(u_2n-1-u_2n) = послед-ть, состав-я из четных частич-х сумм – возраст-я = u₁–(u₂– u₃) + (u₄– u₅)-…-( u_2n-2-u_2n-1) - u_2n< u₁

имеем послед-ть монотонно возр-х сумм <М₁ =>она имеет lim

Рассмотрим нечет. частич. сумму S_2n+1 = S_2n + u_2n+1

lim (n→∞) S_2n+1 = lim (n→∞) S_2n + lim (n→∞) u_2n+1 = S

Чтд.

Σ^∞_n=1 (-1)ⁿ/n – знакочеред. ряд

u_n = 1/n, u_n+1 = 1/(n+1)

u_n > u_n+1

lim (n→∞) u_n = lim (n→∞) 1/n = 0

№27

(1)Σ^∞_n=1u_n – числа u и n могут иметь произвол. знаки

(2)Σ^∞_n=1 |u_n| - ряд из абсолют. знач-й ряда (1)

Обозначим ч/з S_nn-ную частич. сумму 1-го ряда и ч/з σ_n – 2-го ряда.

|S_n| = | Σⁿ_k=1u_k| ≤ Σⁿ_k=1|u_k| = σ_n

|S_n|≤ σ_n

Опред-е: если д/ряда (1) сход-ся ряд, состав-й из абсолют. знач-й членов ряда (1) (т.е. ряд 2) , то ряд 1 наз-ся абсолютно сход-ся рядом. Если же ряд 1 сход-ся, а ряд 2 расх-ся, то ряд 1 наз-ся условно сход-ся рядрм.

№28

Ряды можно составлять и из ф-ий – функц-е ряды: Σ^∞_k=1f_k(x)

Выберем нек. (∙)х этой области опред-я, получим числ. ряд. Мн-во тех (∙)-ек х, д/кот. соотв-е числ. ряды сход-ся, наз-ся областью сход-ти функц. ряда.

f₁(x₀)+ f₂(x₀)+…+ f_n(x₀)+…= S(х₀)

Ч/з S(х) будем обознач. ф-ию, опред. на области сход-ти, кот. наз-ся суммой эт. ряда.

Степенным рядом наз-ся Σ^∞_n=0 С_n(х-х₀)ⁿ(1)

Числа С_n-ные наз-ся коэф-ом степ. ряда, число х₀ наз-ся центром степ. ряда.

В (∙)х=х₀ степ. ряд сход-ся.

Теорема Абеля: утвержд.1: если ряд 1 сход-ся в нек. (∙)х₁, то он сход-ся в люб. (∙)х, удовл-ей нерав-ву |х-х₀|<|х₁-х₀|.

утвержд.2: если ряд 1 расх-ся в нек. (∙)х₂, то он расх-ся в люб. (∙)х, удовл-ей нерав-ву |х-х₀|>|х₂-х₀|.

Областью сход-ти степ-го ряда явл-ся интервал с центром в (∙)х₀ (х₀ – R, х₀ + R), число R-max расстояние от (∙)х₀ до (∙), где ряд сх-ся – радиус сход-ти степ. ряда.

R = lim (n→∞) |C_n|/|C_n+1| - правило д/нахожд. радиуса сход-ти.

№29

Св-ва степ. рядов:

1) В интервале сход-ти степ. ряда ряд сход-ся абсолютно.

2) В интервале сход-ти степ. ряда ряд сход-ся к непрерыв. ф-ии.

3) Степ. ряд можно почленно диффер-ть. Получ-й при этом нов. степ. ряд будет сход-ся в том же самом интерв-ле к ф-ии , кот. явл-ся производ-й суммы исход. степ. ряда.

Σ^∞_n=0C_n (х-х₀)ⁿ = S(x)

Σ^∞_n=0C_nn(х-х₀)^n-1 = S’(x)

4) Степ. ряд можно почленно интегрировать, при этом получ-й новый степ. ряд сход-ся в том же интервале к ф-ии = ∫ от ф-ии исход. ряда.

Σ^∞_n=0 ∫C_n (х-х₀)ⁿdx = ∫S(x)dx

Σ^∞_n=0C_n/(n+1)∙(х-х₀)ⁿ⁺¹ = ∫S(x)dx

№30

R может = люб. числу от 0 до +∞.

Σ^∞_n=0C_n (х-х₀)ⁿ = S(x)

(х₀ – R, х₀ + R) – интерв.

S(х₀) = С₀

С₁ + 2С₂ (х-х₀) +3С₃(х-х₀)² +…= S’(x); С₁= S’(х₀)

С₂ + 3∙2С₃ (х-х₀) +4∙3С₄(х-х₀)² +…= S”(x); С₂= S”(х₀)/2

С_n = S⁽ⁿ⁾(х₀)/n!

S(х) = Σ^∞_n=0S⁽ⁿ⁾(х₀)/n! ∙ (х-х₀)ⁿ – ряд Тейлора д/ф-ии S(х)

№31

Опред-е: диф-м ур-м наз-ся ур-е, связывающее искомую ф-ию одной или неск-х переменных, эти переменные и производ-е различ. порядков дан. ф-ии.

Если исход. ф-ия зависит от 1 перемен. => ур-е обыкновенное, если от 2 и более перемен. => ур-е в частных производных.

F’(x) = f(x)

G(x, y, y’,…y⁽ⁿ⁾)=0 – общая запись обык. диф. ур-я

Опред-е: решением диф-го ур-я наз-ся такая ф-ия у, кот. при подстановке ее в ур-е превращ. его в тождество.

у”+y =0

y=sinx

Задача о нахождении реш-я диф. ур-я наз-ся задачей интегриров-я дан. диф. ур-я. График реш-я диф. ур-я наз-т интегральной кривой. Реш-е, зависящее от произвольных const наз-ся общим реш-м диф. ур-я.

№32

Опред-е: диф. ур-е 1-го порядка наз-ся диф. ур-м с разделяющимися переменными, если оно может быть записано в одном из след. видов:

(*) dy/dx = f(x)g(y); dy/g(y) = f(x)dx

(**) M(x)N(y)dx + P(x)Q(y)dy = 0; M(x)dx/P(x) = Q(y)dy/N(y)

(*)∫dy/g(y) = ∫f(x)dy

(**) ∫M(x)dx/P(x) = -∫Q(y)dy/N(y)

№33

Опред-е: диф. ур-е 1-го порядка наз-ся однородным, если его можно записать в след. виде: y’ = f(y/x)

Ф-ия f(x, y) наз-ся однород. ф-ией порядка k, если f(dx, dy) = α^kf(x, y).

Пример:

y’ = (x+2y)/x

y’ = 1+2y/x

Пусть y/x = z,

y = zx

y’ = z+xz’

z+xz’ = 1+2z

xz’ = 1+z

dz/(1+z) = dx/x

∫dz/(1+z) = ∫dx/x

ln|1+z| = ln|x|+lnC

|1+z| =|x|C

z = xC – 1

y/x = xC – 1

y = x²C - x

№34

Опред-е: диф. ур-е 1-го порядка, им. вид y’+f(x)y = g(x), наз-ся линейным диф-м ур-м.

Если g(x) ≡ 0, то соотв. ур-е наз-ся однород. лин. ур-м.

Если g(x) ≠ 0, то ур-е наз-ся неоднородным.

Реш-е им. вид:

y(x) = u(x)v(x)

y’ = u’v + uv’

u’v + uv’ + f(x)uv = g(x)

u’v + u(v’ + f(x)v) = g(x)

v’ + f(x)v= 0

dv/v = -f(x)dx

v = -∫f(x)dx

№35

В нек. случаях реш-е диф. ур-я 2-го порядка можно свести к послед. реш-ю 2-х диф. ур-й 1-го порядка. В этих случаях говорят, что диф. ур-е 2-го порядка допускает пониж. порядка ур-я.

а) y” = f(x) – прав. частьна зависит от у

y’ = z

z’ = ∫f(x)dx

y’ = ∫f(x)dx

б) если в записи ур-я 2-го порядка не входит искомая ф-ия у

G (x, y’, y”) = 0

y’ = z

G (x, z’, z”) = 0

в) когда в ур-ии нет в явном виде независ. перемен. х

За независ. перемен. взять у, а за нов. ф-ию – zy’.

G (y, y’, y”) = 0

y’ = z

2yy” = (y’)² +1

y’ = z(y)

y” = z’_y∙ y’ = z’z

2yz’∙z = z² +1

2yz∙dz/dy = z² +1

2zdz/(z² +1) = dy/y

ln|z² +1| = ln|y| + ln|C₁|

z² +1 =yC₁

z = √( yC₁ – 1)

dy/dx = √( yC₁ – 1)

∫ dy/√( yC₁ – 1) = ∫dx

y = [(x+C₂)²/4 + 1] ∙ 1/C₁

№36

Пусть z = f(x,y) – ф-ия 2-х переменных

z’_x; ∂z/∂x– частная производ. по х

z’_у; ∂z/∂у – частная производ. по у

Полный дифф-ал 1-го порядка от ф-ии z: dz = ∂z/∂x ∙ dx + ∂z/∂у∙ dy

Пример:

z = sin(x³y)

z’_x= cos(x³y) ∙3x²y

z’_у= cos(x³y) ∙ x³

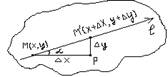
dz = 3x²ycos(x³y)dx + x³ cos(x³y)dy

№37

M₀ (x₀, y₀)

M (x₀+∆x, y₀)

f(M) – f(M₀) = f(x₀+∆x, y₀) - f(x₀, y₀) = ∆_x f(x₀, y₀) – част. приращ. поперемен. х

f(x₀+∆x, y₀) - f(x₀, y₀) = ∆_у f(x₀, y₀)- част. приращ. по перемен. у

Опред-е: част. произв-й ф-ии 2-х переменных по перемен. х наз-ся предел отнош-я частного приращ-я по этой перемен. к приращ. этой перемен. при усл-ии когда предел:

lim(∆x→0) ∆_xf(x, y)/ ∆x = ∂f/∂x

№38, №41

Пусть дана ф-ия 2-х перемен. z=f(x, y)

∆z = f(x +∆x, y +∆y) – полн. приращ. ф-ии

ρ = √[(∆x)² – (∆y)²]

Если расст. → к 0, ∆x и ∆y→ к 0.

Если ∆x и ∆y→ к 0, то ρ→0.

В этом прир-ии ф-ии глав.лин. часть – выр-е: ∆z = f(x +∆x, y +∆y) - f(x, y) = А∙∆x + В∙∆у + O(ρ)

Если при ρ→0 можно подобрать вел-ны А и В, не завис. от ∆x и ∆y, такие, что А∙∆x + В∙∆у будет отлич-ся от полн. приращ-я ф-ии ∆z на вел-ну беск. малую высшего порядка по срав. с ρ, то ф-ия z наз-ся диффер-ой ф-ией, а глав. лин. часть его приращ-я наз-ся полным диф-ом ф-ии z(dz).

А∙∆x + В∙∆у = dz

Теорема1: диф-л ф-ии= сумме произвед-й: част. произв-е ф-ии на диф-л этой перемен.

dz = ∂z/∂x ∙ dx + ∂z/∂y ∙ dy

Теорема2: если ф-ия z = f(x,y) обладает непрерывными частными произв-ми ∂z/∂x и ∂z/∂y в заданной области, то эта ф-ия диф-ма в дан. области и ее диф-ал выр-ся: dz = ∂z/∂x ∙ dx + ∂z/∂y ∙ dy

P(x, y)dx + Q(x, y)dy (*)

{∂f(x,y)/∂x = P(x, y)

{∂f(x,y)/∂y = Q(x, y)

Теорема3: д/того, чтобы выр-е (*) было полн. диф-ом нек. ф-ии f(x,y) необходимо, чтобы в заданной области тождественно вып-сь соотн-е: ∂Q/∂x = ∂P/∂y (**) – необх. усл-е полн. диф-а.

№39

z = f(x,y) определена в нек. области G

На луче l выберем (∙)М(х,у) и будем перемещ-ся из (∙)М(х,у) в (∙)М’(х+∆x,у+∆y)

∆_ez = f(х+∆x,у+∆y) - f(х,у)- приращ-е ф-ии в заданном направ-ии l.

ρ(M, M’) = ∆l

∆x = ∆l∙cosα

∆x = ∆l∙sinα = ∆l∙cos(π/2 – α)

π/2 – α = β

∆x = ∆l∙cosα

∆y = ∆l∙cosβ

cosα и cosβ – направляющие cos-ы дан. вектора

Опред-е: вел-на lim (∆l→0) ∆_ez/∆l = ∂z/∂l наз-ся производ. ф-ии z по направ. l. Эта вел-на задает скорость измен-я ф-ии в задан. направ-ии l.

lim (∆l→0) ∆_ez/∆l = ∂z/∂l = ∂z/∂x∙ cosα + ∂z/∂y∙ cosβ

№40

Опред-е:max-ом ф-ии f(x,y) наз-ся такое знач-е этой ф-ии, принимаемое в нек. f(x₀,y₀), кот. больше всех ее знач-й f(x,y), принимаемых дан. ф-ией в (∙)-ах нек. окрестности f(x₀,y₀).

Опред-е:min-ом ф-ии f(x,y) наз-ся такое знач-е этой ф-ии, принимаемое дан. ф-ией, кот. меньше всех знач-й ф-ии, принимаемых ею в (∙)-ах нек. окрестности f(x₁,y₁).

Теорема1 (необх. усл-е экстремума): в (∙) экстремума ф-ии неск. переменных каж. ее частная произв-я 1-го порядка либо =0, либо не сущ-т.

(∙)-ки, в кот. частная произв-я 1-го порядка одновременно =0, и не сущ-т, наз-ся критич. д/дан. ф-ии или подозрит. на экстремум.

Опред.: наиб. и наим. знач. ф-ии в дан. области g наз-ся абсолютным (глобальным) экстремумом ф-ии в дан. (∙).

Теорема Вейерштрасса: ф-ия, непрерыв. в огранич. и замкнутой области достигает своего наиб. и наим. знач. либо в критич. (∙) этой ф-ии, лежащей в области, либо на границе области.

Теорема3 (достат. усл-е экстремума ф-ии 2-х перемен.): пусть ф-ия z = f(x,y) непрерыв. в нек. критич. (∙) (x₀, y₀), а также определена и непрерывна в нек. ее окрестности. Пусть кроме того ф-ия имеет непрерыв. част. произв. 2-го порядка в этой (∙) и пусть

f”_xx(x₀, y₀) = A

f”_xy(x₀, y₀) = B

f”_yy(x₀, y₀) = C,

тогда если число (АС-В²)>0, то в дан. (∙) будет экстремум, причем, если А<0, то в дан. (∙) будет max, если А>0, то в дан. (∙) будет min.

Если (АС-В²) <0, то в дан. (∙) экстремума нет.

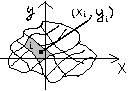
Если (АС-В²) =0, то вопрос ост-ся открытым.

№42

z = f(x,y)

Д- плоскость, огранич. или неогранич.

Разделим областьД:

∆S_i

∆S = max{∆S_i}

I = Σⁿ_i=1f(x_i, y_i)∆S_i – интегр-я сумма д/ф-ии z = f(x,y) (1)

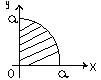
Опред-е: если сумма (1) им. предел при n→∞, так, чтобы ∆S→0 и этот предел не зависит от выбора сп-ба разбиения области Д и от выбора внутр. (∙)-ек в каж. части разбиения, то ф-ия f(x,y) наз-ся интегрируемой по обл. Д, а сам предел наз-сядвойным ∫ по обл. Д от ф-ии f.

lim(∆S→0) Σⁿ_i=1f(x_i, y_i)∆S_{i =} ∫_Д∫ f(x,y)dS, где dS – беск. малое приращ. площади, диф-л S.

Геометрич. смысл 2-го ∫:

∆S_i = ∆ x_i∙ ∆y_i

Σ^m_j=1Σⁿ_i=1f(x_i, y_i)∙ ∆ x_i∙ ∆y_i

∫_Д∫ f(x,y)dS = ∫_Д∫f(x,y)dxdy – повторный ∫

_a∫^bdx _g(x) ∫^f1(x)f(x, y)dy (из 1)

∫_Д∫ f(x,y)dxdy = _c∫^d_g(y) ∫^r(x)f(x,y)dx

∫_Д∫ dxdy = S_д - замечание