Рекурсивные функции
| Загрузить архив: | |
| Файл: ref-22957.zip (55kb [zip], Скачиваний: 94) скачать |
Содержание
Введение ------------------------------------------------------------------------2
Рекурсивные функции ------------------------------------------------------------------3
Определение -----------------------------------------------------------------------------4
Теорема 2. --------------------------------------------------------------------5
Предложение 1. -------------------------------------------------------------------------5
Доказательство 1. --------------------------------------------------5
Предложение 2. --------------------------------------------------------------------------5
Доказательство 2. ------------------------------------------------------6
Предложение 3. -------------------------------------------------------------------------------------------------------8
Предложение 4. -----------------------------------------------------------------------------9
Доказательство 3. ---------------------------------------------------------------------9
Заключение-------------------------------------------------------------------------------------------11
Список Литературы --------------------------------------------------------------------12
Введение
В этом реферате мы приведем способ уточнения понятия вычислимой функции который можно назвать алгебраическим, так как определяемый класс функций будет порождаться из некоторых простейших функций с помощью некоторых операций. Под частичной функцией мы понимаемf: X®w, где ХÍwn для некоторого nÎх.
Так же рассмотрим частично рекурсивные функции совпадающие с классом функций, вычислимых, по Тьюрингу.
Ниже приведём множество примеров и доказательств этой теоремы таких как:
g=Sn,k-1(f, I na1,…,I nak)
и предложения как на пример:
1)Пулъместные функции n, nÎw;
2)двухместная функция сложения +;
3)двухместная функция умножения • ;
4)двухместная функция усеченной разности •,
___
5)одноместные функции sg и sg,
6)двухместнаяфункция идентификации6.
Также я приведу определенные понятия рекурсивного предиката, как предиката, представляющая функция которого является рекурсивной. Таким образом, рекурсивные предикаты это в точности такие предикаты RW, для которых эффективно решается проблема вхождения, т. е. проблема определения по заданной n-ке чисел < m1,..., mn >.
Рекурсивные функции
Напомним, что под частичной функцией мы понимаем здесь, всякое,
отображение
f: X®w, где ХÍwn для некоторого nÎх. Число п в этом, случае называется
местностью частичной функции fи обозначается через v(f). Если
f: X®w — частичная функция, то будем называть f нигде не
определенной при X = Æ и всюду определенной при. X = wv(f)*). Всюду
определенную частичную функциюв дальнейшем будемназывать
просто функцией. Частичную функцию местности п будем называть n-
местной частичной функцией. Мы допускаем случай, когда n = 0. Тогда 0-
местная функция f: w°®w будет состоять из одной пары <Æ, п> для
некоторого nÎw и часто будет отождествляться с числом n. Всюду в даль-
нейшем буквы т, k, n, I и j ], возможно с индексами, будут обозначать
натуральные числа.
Пусть f: X®
w
— n-местная
частичная функция. Если
когда обе части равенства определены и равны, либо обе части
равенства не определены.
Пусть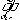 
семейство всех n - местных частичных
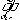функций,а = U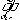n,
семейство всех частичных функции.
Определим на
семействе 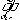всех частичных функций операторы S, R, М, которые сохраняют
вычислимость функций.
Пусть n, kÎw, f—(n+1)-местная частичная функция, go,..., gn — k-
местные частичные функции. Определим k-местную частичную функцию h
следующим образом: h(m1,.., mk) не определено, если хотя бы одна из
частичных функций go,..., gn не определена на _
всеgo,...,gn определенына < m1,.., mk>, то h(m1,.., mk)=f(go(m1,.., mk)…,gn(m1,.., mk)).
Будем говорить,
что h получена
регулярной суперпозицией из f, g0, …, gn и обозначать это следующим образом h=Sk,n(f,g0, …, gn). Оператор (регулярной суперпозиции)- Sk,n является всюду определенным отображением из 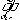n+1 X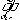n+1k в 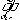k и сохраняет вычислимость, т.е. если частичные функции fÎ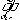n+1;g0, …, gnÎ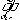kвычислимы,
то и частичная функция
Sk,n (f,g0, …, gn) вычислима. Верхние индексы, у оператора S будут опускаться и
вместо S(f, g0, …, gn) будет, как правило, использоваться более привычное, но менее точное обозначение f(g0,...,gn). Пусть nÎw,f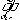În,gÎ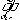n+2.Определим по f и g(n + 1) - местную частичную функцию h так, что для любых m1,..,
mnÎw
h(m1,.., mn,0)=f(m1,.., mn);
h(m1,..,
mn
,k+1)
не
определено, если h(m1,..,
mn, k) неопределено и h(m1,..,
mn, k+1) = g(m1,..,mn,k), h(m1,..,
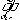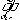mn,k)), если h(m1,.., mn, k) определено. Очевидно, что h однозначно определена по f и g и вычислима, если вычислимы/ и указанное определение h по / и g задает оператор h=Rn+1:nXn+2®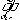n+1 который назовем оператором примитивной рекурсии. Про h=функцию h = Rn+1(f, g) будем говорить, что она получила примитивной рекурсией из функций f и
g. Верхний индекс у оператора Rn+1 будем опускать.
Пусть nÎw,fÎ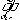n+1. Определим по f такую n-местную частичную
функцию g, что для любых k, m1,..,
mnÎw тогда и только тогда,
когда f(m1,..,
mn,0)=0
и k=0
или k>0
и f(m1,..,
mn,0)
определены и не
равны нулю, а f(m1,..,
mn,k)=0. Ясно, чтотакая функция д существует и однозначно определена по f;
кроме того, если f — вычислимая функция, то из определения g видно, как вычислять g. Таким образом, задан оператор Mn — оператор минимизации — из 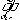n+1
в 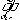nесли g= Mn (f) то будем говорить, что g получена минимизацией из f .
Базисными функциями называются функции о, s, Inm(1≤m≤n) где о —
одноместная функция, которая па любом n принимает значение 0, s — одноместная функция, принимающая на числе n значение n+1, aInm— n-местная функция, принимающая на наборе (k1,…,kn) значение km. Очевидно, что базисные функции вычислимы.
Определение.
Частичная функция f называется частично рекурсивной,
если существует такая конечная последовательность частичных функций
g0, …, gk что gk=fи каждая gi, i≤k либо базисная, либо получается из
некоторых предыдущих регулярной суперпозицией, примитивной рекурсией
или минимизацией. Эта последовательность g0, …,gk называется определяющей последовательностью для f. Если для всюду определенной
частично рекурсивной функции f существует определяющая
последовательность, состоящая только из всюду определенных функций, то f называется рекурсивной.
В следующем параграфе будет доказано, что любая всюду определенная
частично рекурсивная функция является рекурсивной.
Из данного определения и приведенных выше замечаний о сохранении
вычислимости операторами S, R, М легко следует, что всякая частично
рекурсивная функция является вычислимой.
Обратное утверждение носит название тезиса Чёрча: любая вычислимая частичная частично рекурсивна.
Исторически именно это утверждение было первым точным математическим
определением понятия (алгоритмически) вычислимой функции.
Имеет место следующая теорема, доказательство которой мы опустим из-
за его громоздкости.
Теорема 2
Класс частично рекурсивных' функций совпадает с классом функций,
вычислимых, по Тьюрингу.
Таким образом, тезис Тьюринга эквивалентен .тезису Чёрча.
Пусть k, nÎw а — некоторое отображение множества {1,...,k} в множество {1,...,n} f— k-местная частичная функция. Будем говорить, что n-местная частичная функция g получена из f подстановкой ее, если для любых m1,.., mnÎw имеет место соотношение:
g(m1,.., mn))=(ma1,..,mak).
Будем использовать в этом случае обозначение g=fa
Предложение1.
Если f — частично рекурсивная функция и g получена из fподстановкой а, то g частично рекурсивна.
Доказательство 1.
Легко проверить, что еслиg=fa, то
g=Sn,k-1(f, I na1,…,I nak)
Предложение2.
Следующие функции рекурсивны:
1)Пулъместные функции n, nÎw;
2)двухместная функция сложения +;
3)двухместная функция умножения • ;
4)двухместная функция усеченной разности •, определенная следующим
образом:
___
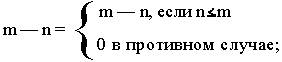
5)одноместные функции sg и sg, определенные следующим образом:
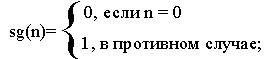
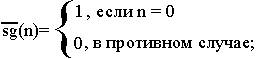
двухместнаяфункция идентификации6, определенная следующим образом:
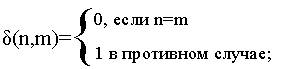
Доказательство 2.
Покажем рекурсивность нуль - местной функции {< Æ, n>} индукцией по n. Функция{< Æ, 0>}равна M(0). Если функция {< Æ, n>} рекурсивна, то рекурсивна функция S{< Æ, n>}={< Æ, n+1>}. Так как n+0 = n и n+(m+1) то функция + равна R(I11S(I33)). Из равенств n•0=0 и n•(m+1) =
n•m+nследует, что функция равна R(0,I11 +I33)
Для того чтобы показать рекурсивность —
усеченной
разности
рассмотрим одноместную функцию -- 1 определённую
так:
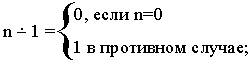
Она равна R(0,I21) поэтому рекурсивна. Так как n — (m+1)=(n — m) — 1, то функция -- равна R (I11,I33 – 1) следовательно, также является рекурсивной.
Рекурсивность функций следует из равенств sg = R(o,s (0(I21))) и sg=R(1,0(I21)). Пусть a:{1,2} ®{1,2}такого что a(1=2), a(2=1), af— функция
полученнаяиз функции -- подстановкойа. Тогда дляфункцииδ
справедливо равенство δ=S(sg), S(+,--,f)). Из рекурсивности функций sg — и предложения получаем, что функция идентификации δявляется рекурсивной.
Для задания, рекурсивныхфункций и изучения их свойств удобно-
пользоваться специальнымформальным языком Rå.
Пусть V={UiIiÎw} — множество переменных, элементы лоторого
будем обозначать буквами х, у, z, w, и, возможно с индексами.
Пусть å(R,F,M) — некоторая конечная сигнатура такая, что
FÊF0={0,s,+,•) где 0 символ нульместной функции, s— символ одноместной функции, +, • — символы двухместных функций;RÊR0 ={<}, где < символ двухместного предиката.
Определение выражений, (синтаксис) языка Råбудет зависеть еще и от семантики этого языка. Поэтому определение синтаксиса и семантики будет вестись, одновременно, но прежде всего зададимся фиксированной алгебраической системойWåсигнатуры åс основным множеством w и такой, что значения символов сигнатуры å0 = (R0,F0,Mn) совпадают с функциями и предикатом, обозначенными этими символами ранее (например, символу • соответствует операция умножения натуральных чисел).
Итак, будем одновременной индукцией определять понятие å-терма, å-формулы (более точно было бы говорить об Wåтермах и Wå-формулах), множества свободных переменных FV(t) и FV(j) å-терма t и å-формулы j соответственно, натуральное число t[h] и истинностное значение j[h]Î{и,л} для всякой интерпретации®w где ХÍV,FV(t) FV(j)ÍX;
а) символ 0 является å-термом, FV(0=Æ) и 0[h=0];
б)переменная хÎУявляется å-термом, FV(x)={x}, x[h]=h(x);
в)если fÎF — n-местный функциональный символ, t1,…,tn å-термы; то
å-терм f(f1,...,tn); FV(f(t1,…,tn))=FV(t1)U…UFV(tn); F(t1,…,tn) [h]=fWå (t1[h],…,tn[h])
здесь fWå-n местная операция Алгебраической системы Wåсоответствующая сигнатурному символу f;
г) если
(Q—
n-местный
предикатный символ из Rat1,…,tn
å-термы, то Q(t1,…,tn) å-формула, FV(Q(t1,…,tn))=FV(t1)U…UFV(tn); Q(t1,…,tn) [h] здесь QWå— n-местный предикат, соответствующий в
алгебраической
системе Wå предикатному символу Q;
д)Если t1,…,t2 å-термы, t1≈t2å-формула, FV(t1≈t2) =FV(t1)UFV(t2), (t1≈t2)
[h] = и <=> t1[h]=t2[h];
е)Если j и ψ å-формула то ┐j,(j,t,ψ) для tÎ{∧,∨,®}å-формулы, fV(┐j) = FV(j), FV(j,t,ψ)=FV(j) U FV(ψ) и (┐j)[h] = ┐(j[h]) где ┐ ∧,∨,®операции определены на множестве {и,л} таблицей (1) c заменой «о» на «л» и «1» на «и»
ж)Пусть jå-формула, xÎV и для любой интерпретации h1:X®w для которой xÏX и FV(j)ÍXU{x}cсуществует такое же n, что j[h] = и для h=h1
U{
Как обычно, в место +(t1,t2)•(t1,t2))
будем писать (t1+t2)((t1•t2)) и
(t1 сокращениями для
термов и формул,
принятыми варифметике
и исчислении
высказываний (например, вместо (x+((z•z)+(x•y))) и
((j∧ψ)®jбудем писать соответственно x+z2+xy и (j∧ψ)®j). Для å-формулы j и интерпретации h;
x®w
FV(j)Íx, часто вместо «j[h] = и» будем писать «j[h] истинно» или просто «j[h]». А вместо «j[h] = ∧»
будем писать «j[h]
ложно» или «┐j[h]». ПустьQ — å-терм или (å-формула).
Вхождение переменной x в Qназывается свободным, если оно не находится в пол слове
видаmxjявляющемся å-термом. Если вхождение переменной в не
является свободным,
то оно называется связанным. Легко проверить, что множество FV(Q)состоит в точности из переменных, имеющих
свободные вхождениям
в Q. Пусть
вQå-терм
(å-формула), x1,…,xnÎV- различные переменные, t1,…tnå-терм
такие, что для
любого iÎ{1,…,n} и любого yÎV(t1)
ни одно свободное вхождение в Q переменной Xi не содержится в терме вида
являющемся myj под
словом Q. Ю. Л.
Ершов, Е. Л. Палютиа Индукцией
по построению å-терма
и å-формулы без труда устанавливается следующее. Предложение 3. Если Qå-терм (å-формула) х1,..,хnÎV — различные переменные, t1,...,tn — å-термы такие, что для Q, х1,..,хn, t1,...,tn выполнены сформулированные выше условия, то 1) Q1= К сожалению, условия для возможности подстановки å-термов вместо Предложение 4. Если Q и Q' — конгруэнтные å-тёрмы или å-формулы, то FV(Q=FV(Q’))для любой интерпретации h:FV(Q)®wимеем Q[h]=Q’[h]. Доказательство 3. Индукциейпо длине Qлегко показать, что если Q1 получается из Q заменой связан ной переменной, то утверждение предложения
истинно. Далее
индукция по длине последовательности Q0,…,Qnиз предыдущего определения. Отметим,
что для любого å-терма
( å-формулы) Q, любого набора попарно различных переменных x1,…,хn любых å-термов
t1,...,tn существует å-терм (å-формула)
Q' такой (такая), что Q' конгруэнтен (конгруэнтна) Q и для Q' выполнены условия для подстановки Напомним,
что подмножество XÍAn называется n-местным предикатом на А. В дальнейшем под предикатами будем
понимать предикаты на w. Если
n-местный предикат, то n-местная
функция nxопределенная следующим образом: для любых m1,…,mnÎw
случаев, называется
представляющей функцией для X. Наряду с представляющей функцией px предиката X часто используют характеристическую функцию
Xх
предиката X,
которая связана с функцией px соотношением Xx= sg(px) предикат X называется рекурсивным, если его пред уставляющая функция px
рекурсивна. Алгебраическая
система Wå называется рекурсивной, если все функции и предикаты, соответствующие символам сигнатуры
å, являются рекурсивными. В
дальнейшем, говоря оå-формулах и å-термах
(определение которых представляющей
функцией для ≈ является функция идентификации δ а представляющей
функцией для < будет рекурсивная функция sg(S(I21) – I22). С каждым å-термом (
å-формулой) можно связать семейство функций (предикатов), которые реализуются функций (предикатов) будем использовать расширение
языка, Råдобавив
новую пару [,] символовквадратных, скобок. Перейдем
к точным, определениям. Еслиt- å-терм дляi¹j то через t[x1,…,хn] будем обозначать n-местную функцию, принимающую на n-ке +
реализует много функций, например, если FV(t)Í{x,y} то [x,y], +[y,x] и [x,y,z], вообще говоря,
различные функции символ [x1,…,хn] играет роль,аналогичную кванторам,он связывает x1,…,хnтак, например, если FV(t)Í{x1,…,хn} и y1,…,ynпопарно
различные переменные, то
имеетместо равенство. t[x1,…,хn] = В этой курсовой было
определено понятие рекурсивного предиката, как предиката, представляющая
функция которого является рекурсивной. Таким образом, рекурсивные предикаты это
в точности такие предикаты RW,
для которых эффективно решается проблема вхождения, т. е. проблема определения
по заданной n-ке чисел Так же рассмотрели
частично рекурсивные функции совпадающие с классом
функций, вычислимых, по Тьюрингу. В этом реферате мы привели способ уточнения понятия
вычислимой функции который можно назвать алгебраическим, так как определяемый
класс функций будет порождаться из некоторых простейших функций с помощью
некоторых операций. Под частичной
функцией мы понимаемf: X®w,
где ХÍwn для некоторого nÎх. Спасибо за то что прочитали эту курсовую, надеюсь вы почерпнули из
прочитанного материала много нового и познавательного. 1.
Марченко С.С. Элементарные
рекурсивные функции. М.: МЦНМО, 2003. 2.
Кузнецов А.В. К теореме о
канонической форме для ординально-рекурсивных функций. В книге Гудстейн Р. Л.
Математическая логика. М.: ИЛ, 1961, с. 149-154. 3.
Смальян Р. Теория формальных
систем. М.: Наука, 1981. 4.
Косовский Н. К. Элементы
математической логики и ее приложения к теории субрекурсивных алгоритмов. Л.,
Из-во Ленинград. ун-та, 1981. 5.
Гжегорчик А. Некоторые классы
рекурсивных функций. В книге: Проблемы математической логики. М., Мир, 1970, с.
9-49.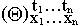 
будет
обозначать результат замены
всех свободных вхождений переменных х1,..,хn наå-термы
- t1,...,tnсоответственно.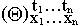является
å-тepм (å-формулой), в такой
для
любой интерпретации h:x®w. В такой, что (FV(Q){х1,..,хn})U…UFV(tn)Íxвыполняется равенство Q1[h]=Q[h] где h’ = {
терм (å-формулу) будем говорить, что Q
получен из Q подстановкой å-
термов t1,...,tn вместо переменных х1,..,хn.
переменных не
всегда выполнены. Чтобы всегда иметь возможность для
подстановки,
введем следующие понятия. Будем говорить, что å-терм (å-
формула) Q
получается из å-терма
(å-формулы) Q, заменой связанной
переменной, если Q получается
из заменой вхождения å-терма
mxjна my(j)xyгде yÎFV(j). å-термы (å-формулы) Q и Q1 называются конгруэнтными, если существует такая последовательность Q0,…,Qnчто Qo = Q1 ; Qo = Q’;QI+1 ,I
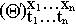пользуясь этим свойством и предложением 4,будем впредь использовать запись 
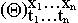, не заботясь о выполнении условий на связанные переменные считая, что если
эти условия не выполнены, то 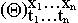есть 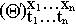для å-терма (å-формулы)Q',
конгруэнтного (конгруэнтной) Q в, причём для Q' все условия для подстановки уже выполнены.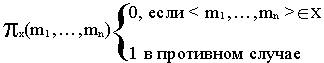
зависит от
фиксированной алгебраической системы Wå, будем
всегда
предполагать,что Wå — рекурсивная алгебраическая система.
Заметим, что
предикаты ≈,< являются
рекурсивными, так как
этим å-термом ( å-формулой). Для
обозначения этих
[ y1,…,yn].Заключение
Список Литературы