Исследование элементарных функций


	Загрузить архив:
	Файл: ref-22983.zip (118kb [zip], Скачиваний: 203) скачать

Красноярский Государственный Педагогический Университет им. В.П. Астафьева.

Реферат

На тему: «Исследование элементарных функций».

Выполнила: Квашенко Д.В.

Проверил: Адольф В.А.

г. Красноярск

2005г.

Содержание:

·Определение элементарных функций…………….3

·Функция и её свойства……………………………………..3

·Способы задания функции……………………………….4

·Определение функции……………………………………..4

·Исследование элементарных функций………....6

а) Линейная функция…………………………….......7

б) Степенная функция…………………………………..8

в) Показательная функция……………………………9

г) Логарифмическая функция……………………..10

д) Тригонометрическая функция………………..11

o Y=sinx……………………………….…11

o Y=cosx…………………………………13

o Y=tgx…………………………………..14

o Y=ctgx…………………………………15

е) Обратно тригонометрическая функция..16

o Y=arcsinx…………………………….16

o Y=arccosx……………………………17

o Y=arctgx……………………………..18

o Y=arcctgx…………………………….19

·Список литературы………………………………………..20

Определение элементарных функций.

Функции С (постоянная), xⁿ, а^х, 1оg_а х, sin х, соs х, tg х, ctgx, аrcsin х, аrccos х, аrctg хназываются простейшими элементарными функциями.

Применяя к этим функциям арифметические действия или операции функции от функции, мы будем получать новые более сложные функции, которые называются элементарными функциями.

Например, у = sin(xⁿ) — элементарная функция.

Элементарные функции нам известны из школьной математики.

Функция, и её свойства:

Функция - зависимость переменной у от переменной x, если каждому значению х соответствует единственное значение у.

●Переменная х - независимая переменная или аргумент.

●Переменная у - зависимая переменная.

●Значение функции - значение у, соответствующее заданному

значению х.

●Область определения функции - все значения, которые принимает независимая переменная.

●Область значений функции (множество значений)-все значения, которые принимает функция.

●Функция является четной - если для любого х из области определения функции выполняется равенство f(x)=f(-x).

●Функция является нечетной - если для любого х из области определения функции выполняется равенство f(-x)=-f(x).

●Возрастающая функция - если для любых х₁ и х₂, таких, что х₁< х₂, выполняется неравенство f(х₁)2).

●Убывающая функция - если для любых х₁ и х₂, таких, что х₁< х₂, выполняется неравенство f(х₁)>f(х₂).

Способы задания функции:

●Чтобы задать функцию, нужно указать способ, с помощью которого для каждого значения аргумента можно найти соответствующее значение функции. Наиболее употребительным является способ задания функции с помощью формулы у=f(x), где f(x) - заданная функция с переменной х. В таком случае говорят, что функция задана формулой или что функция задана аналитически.

●На практике часто используется табличный способ задания функции. При этом способе приводится таблица, указывающая значения функции для имеющихся в таблице значений аргумента.

Определение функции.

Функция, прежде всего,– это одно из основных понятий математического анализа, и чтобы далее рассматривать различные функции, следует дать определение функции.

Пусть даны две переменные x и y с областями изменения X и Y.Предположим, что переменной x может быть приписано произвольное значение из области X без каких-либо ограничений. Тогда переменная y называется функцией от переменной x в области её изменения X, если по некоторому правилу или закону каждому значению x из X ставится в соответствие одно определенное значение y из Y.

Независимая переменная x называется также аргументом функции.

В этом определении существенны два момента: во-первых, указание области X изменения аргумента x (её называют также областью определения функции) и, во-вторых, установление правила или закона соответствия между значениями x и y (Область Y изменения функции обычно не указывается, поскольку самый закон соответствия уже определяет множество принимаемых функцией значений).

Можно в определении понятия функции стать на более общую точку зрения, допуская, чтобы каждому значению x из X отвечало не одно, а несколько значений y (и даже бесконечное множество их). В подобных случаях функцию называют многозначной, в отличие от однозначной функции, определенной выше.

Для указания того факта, что y есть функция от x, пишут:

y=f (x), y=g (x),y=F (x) и т.п.

Буквы f, g, F, … характеризуют именно то правило, по которому получается значение x, отвечающее заданному y. Поэтому, еслиодновременно рассматриваются различные функции от одного и того же аргумента x, связанные с различными законами соответствия, их не следует обозначать одной и той же буквой.

Хотя именно буква f связана со словом “функция”, но для обозначения функциональной зависимости может применяться и любая другая буква; иногда даже повторяют одну и ту же буквуy: y=y(x). В некоторых случаях пишут аргумент и в виде значка при функции, например,

Если, рассматривая функцию y=f(x), мы хотим отметить её частное значение, которое отвечает выбранному частному значению x, равному f(

F (x)=, g (t)=, то f(1) означает численное значение функции f(x) при x=1, т.е. попросту число g(5) означает число 2, и т. д.

Теперь обратимся к самому правилу, или закону соответствия между значениями переменных, которое составляет сущность понятия функциональной зависимости.

Наиболее просто осуществление этого правила с помощью формулы, которая представляет функцию в виде аналитического выражения, указывающего те аналитические операции или действиянад постоянными числами и над значением x, которые надо произвести, чтобы получить соответствующее значение y. Этот аналитический способ задания функции является наиболее важным для математического анализа.

Однако будет ошибочным думать, что это – единственный способ, которым может быть задана функция. В самой математике нередки случаи, когда функция определяется без помощи формулы. Такова, например, функция E(x) – “целая часть числа x”. Например,

E (1)=1, E (2,5)=2, E ()=3, E (-)=-4 и. т.,

хотя никакой формулы, выражающей E(x), у нас нет.

Функция, все значения которой равны между собой, называется постоянной. Постоянную функцию обозначают C (f (x) = C).

Функция f (x) называется возрастающей (убывающей) на множестве X, если для любой пары чисел < следует, чтоf (f (f () > f ()).

Функция f(x) называется четной, если область её определения X есть множество, симметричное относительно начала координат, и при любом x из X имеет место равенство f(-x)=f(x).

График четной функции симметричен относительно оси Oy.

Функция f(x) называется нечетной, если область её определения X есть множество, симметричное относительно начала координат, и если при любом x из X имеет место равенство f(-x)=-f(x).

График нечетной функции симметричен относительно начала координат.

Сумма и разность двух четных (нечетных) функций есть функция четная (нечетная).

Действительно, пусть y(x)=f(x) + g(x). Тогда, если f(x) и g(x)– четные, то y (-x) = f(-x) + g(-x) = f (x) + g (x) = y (x). Если же f (x) и g (x) –нечетные функции, то функция y (x) также будет нечетной, y (-x) = f (-x) + g (-x) = -f (x) – g (x) = -[f (x) + g (x)] = -y (x). (Для разности доказательство аналогичное).

Произведение двух четных или двух нечетных функций есть функция четная, а произведение четнойфункции на нечетную– нечетная функция.

В самом деле, пусть y (x) = f (x)*g (x) и f (x) и g (x) – четные функции, тогда y (-x) = f (-x)*g (-x) = f (x)*g (x) = y (x); если f (x) и g (x) – нечетные функции, тоy (-x) = f (-x)*g(-x) = [-f (x)]*[-g(x)] = y (x); если же f (x) – четная, а g (x) – нечетная функции, то y (x) = f (x)*g (-x) = f (x)*[-g (x)] = -y (x).

Функция f (x) называется периодической, если существует число Т x из области определения функции выполняется равенство f (x - T) = f (x) = f (x + T). Число T называется периодом функции. Если T – период функции, то её периодом является также число – T, так как f (x-T) = f [(x - T) +T] = f (x).

Если T – период функции, то её периодом будет также и число kT, где k – любое целое число (k=f (x2T) = f [(x)T] = f (x) = f (x), f (x3T) = f [(x2T) ] = f (x2T) = f (x2T) = f (x);обычно под периодом функции понимают наименьший из положительных периодов, если такой период существует.

Исследование элементарных функций .

Основные простейшие элементарные функции:

· Линейная функция y=kx+b;

· Степенная функция y=xⁿ;

· Квадратичная функция;

· Показательная функция (0 1);

· Логарифмическая функция (0 < a1);

· Тригонометрические функции: sinx, cosx, tgx, ctgx;

· Обратные тригонометрические функции:arcsinx, arccosx, arctgx, arcctgx.

Линейная функция.

y = kx + b

1. Областью определения линейной функции служитмножество R всех действительных чисел, так как выражение kx+b имеет смысл при любых значениях x

2. Множеством значений линейной функции при k¹0 является множество R всех действительных чисел

3. Функция не является ни четной, ни нечетной, так как f (-x) = -kx + b .

4. Функция не является периодической, за исключением частного случая, когда функция имеет вид y=b.

5. Асимптоты графика функциине существуют.

6. Функция возрастает при k>0, функция убывает при k<0.

7. Функция не является ограниченной.

8. График линейной функции y=kx+b – прямая линия. Для построения этого графика, очевидно,достаточно двух точек, например A(0; b) и B(-b/k; 0), если k¹0. График линейной функции y=kx+b может быть также построен с помощью параллельного переноса графика функции y=kx. Коэффициент k характеризует угол, который образует прямая y=kx и положительное направление оси Ox, поэтому k называется угловым коэффициентом. Если k>0, то этот угол острый, если k<0 – тупой; а при k=0 прямая параллельна оси Ox.

9. Точек перегиба не существует.

10. Не существует экстремальных точек.

y=kx+b (k<0) y=kx+b (k>0)

Степенная функция.

Степенная функция с натуральным показателемy=xⁿ,

где n-натуральное число.

1. Область определения функции: D(f)= R;

2. Область значений: E(f)= (0;+∞);

3. Функция является четной, т.е. f(-x)=f(x);

4. Нули функции: y=0 при x=0;

5. Функция убывает при x(-∞;0];

6. Функция возрастает при x[0;+ ∞);

a) нет вертикальных асимптот

b) нет наклонных асимптот

8. Если n-четное, то экстремум функции x=0

Если n-нечетное, то экстремумов функции нет

9. Если n-четное, то точек перегиба нет

Если n-нечетное, то точка перегиба x=0

10. График функции:

a)Если n=2,то графиком функции является квадратная парабола;

b)Если п = 3, то функция задана формулой у = х³. Ее графиком является кубическая парабола;

c)Если п — нечетное натуральное число, причем п1, то функция обладает свойствами теми же, что и у = х³.

[1]

n – четное

n - нечетное

[2]

Рассмотрим свойства степенной функции с нечетным показателем (п1):

1. Область определения функции: D(f)= R;

2. Область значений [0,+∞];

3. Функция является четной, т.е. f(-х)=f(х);

4. Нули функции: у = 0 при х = 0;

5. Функция убывает на промежутке (-∞;0), возрастает на промежутке (0;+∞).

6. График функции: [1]

Рассмотрим свойства степенной функции с четным показателем :

1. Область определения функции: D(f)= R;

2. Область значений: E(f)= R;

3. Функция является нечетной, т.е. f(-х)=-f(х);

4. Нули функции: у = 0 при х = 0;

5. Функция возрастает на всей области определения.

6. График функции: [2]

Показательная функция.

Y = a^x

1.Область определения функции: -∞ < х < +∞

2.Множество значений функции: 0 < y < +∞

3.Функция ни четная, ни не чётная, так как f(-x) = a^-^x

4.Функция не является периодической.

5.Асимптоты графика функции:

Вертикальных асимптот не существует,

Горизонтальная асимптота у = 0

6.Если а > 1, то функция возрастает на промежутке -∞ < x < +∞ (на рис.1);

7.если 0 < a < 1, то функция убывает на промежутке -∞ < x < +∞ (на рис. 2);

8.Точка (0; 1) – единственная точка пересечения с осями координат.

9. Не существует точек перегиба.

10. Не существует экстремальных точек.

[1]

Логарифмическая функция.

Y = log_ax

1. Область определения функции: 0 < x < ∞

2. Множество значений функции: -∞ < y < +∞

3. Функция ни четная, ни нечетная, так как f(-x) = log_a(-x)

4. Функция не периодическая

5. Асимптоты графика функции:

Вертикальные асимптоты х = 0

Горизонтальных асимптот не существует

6. Если a > 1, то функция возрастает на промежутке 0 < x < +∞ (на рис.1);

если 0 < a < 1, то функция убывает на этом же промежутке (на рис.2);

7. Точка (1; 0) – единственная точка пересечения с осями

координат.

8.Не существует точек перегиба.

9.Не существует экстремальных точек.

[2]

[1]

Тригонометрические функции.

Функция y=sinx

Свойства функции y=sinx:

1.Область определения функции: D(f)=R;

2.Область значений: E(f)=[-1;1];

3.Функция является нечетной, т.е. sin(-x) = - sinx;

4.Функция периодическая с положительным наименьшим периодом 2π;

5.Нули функции: sinx = 0 при x = πk, kZ;

6.Функция принимает положительные значения: sinx>0 при xπk; π+2πk), kZ;

7.Функция принимает отрицательные значения: sinx<0 при xπ+2πk; 2π+2πk), kZ;

8.Функция возрастает на [-1;1] при xπk; πk], kZ;

9.Функция убывает на [1;-1] при xπk; πk], kZ;

10. Функция принимает наибольшее значение, равное 1, в точкахx=πk, kZ;

11. Функция принимает наименьшее значение, равное -1, в точкахx=πk, kZ;

12.

a) нет вертикальных асимптот

b) нет горизонтальных асимптот

13. Графиком функции является синусоида.

y=sinx

Функция y=cosx

Свойства функции y=cosx:

1.Область определения функции: D(f)=R;

2.Область значений: E(f)=[-1;1];

3.Функция является четной, т.е. cos (-x) = cosx;

4.Функция периодическая с наименьшим положительным периодом 2π;

5.Нули функции: cosx = 0 при x = πk, kZ;

6.Функция принимает положительные значения: cosx>0 при xπk; πk), kZ;

7.Функция принимает отрицательные значения: cosx<0 при xπk; πk), kZ;

8.Функция возрастает на [-1;1] при xπ+2πk; 2πk], kZ;

9.Функция убывает на [1;-1] при xπk; π+2πk], kZ;

10. Функция принимает наибольшее значение, равное 1, в точкахx=2πk, kZ;

11. Функция принимает наименьшее значение, равное -1, в точкахx=π+2πk, kZ;

12.

a) нет вертикальных асимптот

b) нет горизонтальных асимптот

13. Графиком функции является косинусоида:

y=cosx

Функция y=tgx

Свойства функции y=tgx:

1.Область определения функции: D(f)=R , кроме чисел вида x =πk, kZ;

2.Область значений: E(f)=R;

3.Функция является нечетной, т.е. tg (-x) = - tgx;

4.Функция периодическая с наименьшим положительным периодом π;

5.Нули функции: tgx = 0 при x = πk, kZ;

6.Функция принимает положительные значения: tgx>0 при xπk; πk), kZ;

7.Функция принимает отрицательные значения: tgx<0 при xπk; πk), kZ;

8.Функция возрастает на (-xπk; πk ), kZ;

a) вертикальные асимптоты x=

+ πn

b) наклонных асимптот нет

10. Графиком функции является тангенсоида:

y=tgx

Функция y=ctgx

Свойства функции y=ctgx:

1.Область определения функции: D(f)=R , кроме чисел вида x = πn , где nZ;

2.Область значений: E(f)=R;

3.Функция является нечетной, т.е. ctg (-x) = - ctgx;

4.Функция периодическая с наименьшим положительным периодом π;

5.Нули функции: ctgx = 0 при x = πn, nZ;

6.Функция принимает положительные значения: ctgx>0 при xπn; πn), nZ;

7.Функция принимает отрицательные значения: ctgx<0 при xπn; π +πn), nZ;

8.Функция убывает в каждом из промежутков (πn; π +πn), nZ;

9. a) вертикальные асимптоты x= πn и x=0

b) наклонных асимптот нет

10.

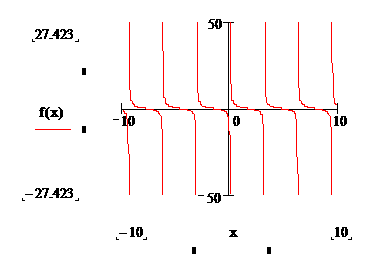Графиком функции является котангенсоида: y= ctgx

Обратно тригонометрические функции.

Функцияy=arcsinx

Свойства функции y=arcsinx:

1.Область определения функции: D(f)=[-1;1];

2.Область значений: E(f)=[-

3.Функция является нечетной, т.е. arcsin (-x) = - arcsinx;

4.Нули функции: arcsinx = 0 при x = 0;

5.Функция возрастает на [-1;1];

6.Функция принимает наибольшее значение при x=1;

7. Функция принимает наименьшее значение при x= -1;

a) вертикальных асимптот нет

b) наклонных асимптот нет

9.График функции y = arcsin x:

y=arcsinx

Функция y=arccosx

Свойства функции y=arccosx:

1.Область определения функции: D(f)=(-1;1);

2.Область значений: E(f)=[0; π];

3.Функция не является ни четной, ни нечетной;

4.Нули функции: arccosx = 0 при x = 1;

5.Функция убывает на (-1;1);

6.Функция принимает наибольшее значение π при x =-1;

7.Функция принимает наименьшее значение 0 при x= 1;

8. a)вертикальные асимптоты x=-1 и x=1

b)наклонных асимптот нет

9.График функции y = arccos x:

y=arccosx

Функция y=arctgx

Свойства функции y=arctgx:

1.Область определения функции: D(f)=R;

2.Область значений: E(f)= (-

3.Функция является нечетной, т.е. arctg (- x) = - arctg x;

4.Нули функции: arctgx = 0 при x = 0;

5.Функция возрастает на R;

6. a) нет вертикальных асимптот

b) наклонные асимптоты y=πn

7.График функции y = arctg x:

y=arctgx

Функция y=arcctgx

Свойства функции y=arcctgx:

1.Область определения функции: D(f)=R;

2.Область значений: E(f)= (0; π );

3.Функция не является ни четной, ни нечетной;

4.Нули функции: arctgx = 0 при x =

5.a) нет вертикальных асимптот

b) наклонные асимптоты y= πn

6.Функция убывает на R;

7.График функции y = arcctg x:

Литература:

üЭ.С. Маркович «Курс высшей математики»

üА.Г. Цыпкин «Справочник по математике»

üМ.М. Потапов, В.В. Александров, П.И. Пасиченко «Алгебра и анализ элементарных функций»