Расчет ректификационной колонны бензол-толуол

[1].

Питание:

где,

- мольные массы бензола и толуола.

Дистиллят:

Кубовый остаток:

Относительный мольный расход питания:

Кривая равновесия (рис. 7.7)[2] точек перегиба не имеет.

Определяем минимальное число флегмы по уравнению:

где,

=0.74 – мольную долю бензола в паре, равновесном с жидкостью питания, определяем по диаграмме Y^* - X.

Рабочее число флегмы:

R=1.3R_МИН+0.3=1.3×1.27+0.3=1.95

Уравнение рабочих линий:

а) верхней (укрепляющей) части колонны:

б) нижней (исчерпывающей) части колонны:

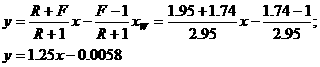
II. Определение скорости пара и диаметра колонны.

Средние концентрации жидкости:

а) в верхней части колонны

б) в нижней части колонны

Средние концентрации пара находим по уравнениям рабочих линий:

а) в верхней части колонны

б) в нижней части колонны

Средние температуры пара определяем по диаграмме t-x, y (рис. 7,6)[3]:

а) при    

б) при     

Средние мольные массы и плотности пара:

а)

б)

Средняя плотность пара в колонне:

Плотности жидких бензола и толуола близки. Температура вверху колонны при y_D=0.965 равняется 82⁰С, а в кубе-испарителе при x_W=0.023 она равна 109⁰С.

Плотность жидкого бензола при 82⁰С ρ_ср=813, а жидкого толуола при 109⁰С ρ_Т=783.

Принимаем среднюю плотность жидкости в колонне

Ρ_Ж=(813+783)/2≈800

Определяем скорость пара в колонне. По данным каталога-справочника «Колонные аппараты» принимаем расстояние между тарелками h=300 мм. Для ситчатых тарелок по графику (рис. 7.2)[4] находим С=0.032.

Скорость пара в колонне по уравнению:

Объёмный расход проходящего через колонну пара при средней температуре в колонне t_ср=(88.7+102.7)/2=95.7⁰С

,

где M_D-мольная масса дистиллята, равная

M_D=0.965×78+0.035×92=78.5

Диаметр колонны:

По каталогу-справочнику «Колонные аппараты» берём D=1900. Тогда скорость пара в колонне будет:

.

III. Гидравлический расчет тарелок.

Принимаем следующие размеры ситчатой тарелки: диаметр отверстий d₀=40. Свободное сечение тарелки (суммарная площадь отверстий) 8% от общей площади тарелки. Площадь, занимаемая двумя сегментными переливными стаканами, составляет 20% от общей площади тарелки.

Рассчитаем гидравлическое сопротивление тарелки в верхней и в нижней части колонны по уравнению:

Δρ= Δρ_сух+Δρ₀+Δρ_пж.

а) верхняя часть колонны.

Гидравлическое сопротивление сухой тарелки:

где ζ=1.82 – коэффициент сопротивления неорошаемых ситчатых тарелок со свободным сечением 7-10%; ω₀=0.6/0.8=7.5– скорость пара в отверстиях тарелки.

Сопротивление, обусловленное силами поверхностного натяжения:

Где σ=20.5×10^-– поверхностное натяжение жидкости при средней температуре в верхней части колонны 88.7⁰С (у бензола и толуола практически одинаковое поверхностное натяжение); d₀=0.004– диаметр отверстий тарелки.

Сопротивление парожидкостного слоя на тарелке:

.

Высота парожидкостного слоя:

.

Величину Δh– высоту слоя над сливной перегородкой рассчитываем по формуле:

,

где V_ж – объёмный расход жидкости, ; ∏ - периметр сливной перегородки, ; k=ρ_пж/ρ_ж – отношение плотности парожидкого слоя (пены) к плотности жидкого, принимаемое приближенно равным 0.5.

Объёмный расход жидкости в верхней части колонны:

,

где M_ср=0.764×78+0.236×92=81.3 – средняя мольная масса жидкости, .

Периметр сливной перегородки ∏ (рис. 15) находим, решая систему уравнений:

где R=0.9– радиус тарелки; ⅔∏b – приближенное значение площади сегмента.

Решение даёт: ∏=1.32; b=0.289. Находим Δh:

.

Высота парожидкого слоя:

Рис. 15. Схема ситчатой тарелки.

Сопротивление парожидкого слоя:

.

Общее гидравлическое сопротивление тарелки в верхней части колонны:

.

б) нижняя часть колонны:

;

,

;

Общее гидравлическое сопротивление тарелки в нижней части колонны:

.

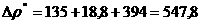
Проверим, соблюдается ли при расстоянии между тарелками необходимое для нормальной работы тарелок условие

Для тарелок нижней части колонны, у которых гидравлическое сопротивление Δρ больше, чем у тарелок верхней части:

Следовательно, вышеуказанное условие соблюдается:

Проверим равномерность работы тарелок – рассчитаем минимальную скорость пара в отверстиях , достаточную для того, чтобы ситчатая тарелка работала всеми отверстиями:

.

Рассчитанная скорость ; следовательно, тарелки будут работать всеми отверстиями.

IV. Определение числа тарелок и высоты колонны.

а) Наносим на диаграмму y- x рабочие линии верхней и нижней части колонны (рис. 16) и находим число ступеней изменения концентрации n_Т. В верхней части колонны , в нижней части , всего 15 ступеней.

Рис. 16. Определение числа ступеней изменения концентрации.

Число тарелок рассчитываем по уравнению:

Для определения среднего к.п.д. тарелок находим коэффициент относительной летучести разделяемых компонентов и динамический коэффициент вязкости исходной смеси при средней температуре в колонне, равной 96⁰С.

При этой температуре давление насыщенного пара бензола Р_б = 1204, толуола Р_Т = 492.5, откуда α = 1204/492.5=2.45.

Динамический коэффициент вязкости бензола при 96⁰С равен 0.27, толуола 0.29. Принимаем динамический коэффициент вязкости исходной смеси = 0.28= 0.28×10^-3.

Тогда

По графику находим (рис. 7.4)[5] η = 0.53. Длина пути жидкости на тарелке (рис. 15)

.

По графику (рис. 7.5)[6] находим значение поправки на длину пути Δ=0.105. Средний к.п.д. тарелок:

Для сравнения рассчитаем средний к.п.д. тарелки η₀ по критериальной формуле, полученной путем статической обработки многочисленных опытных данных для колпачковых и ситчатых тарелок:

В этой формуле безразмерные комплексы:

где – скорость пара в колонне, ;

– относительная площадь свободного сечения тарелки;

– высота сливной перегородки, ;

и – плотности пара в жидкости, ;

– коэффициент диффузии легколетучего компонента в исходной смеси, м²/с;

– поверхностное натяжение жидкости питания, .

Физико-химические константы отнесены к средней температуре в колонне. Предварительно рассчитаем коэффициент диффузии:

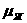В нашем случае: =1; =0.28=0.28×10^-3; =84; 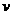=6×14.8+6×3.7-15=96; =95.7+273=268.7.

Коэффициент диффузии:

.

Безразмерные комплексы:

Средний к.п.д. тарелки:

что близко к найденному значению .

Число тарелок:

в верхней части колонны

в нижней части колонны

Общее число тарелок =26, с запасом =30, из них в верхней части колонны 14 и в нижней части 16 тарелок.

Высота тарельчатой колонны:

.

Общее гидравлическое сопротивление тарелок:

V. Тепловой расчет установки.

Расход теплоты, отдаваемой охлаждающей воде в дефлегматоре-конденсаторе, находим по уравнению:

Здесь

где и - удельные теплоты конденсации бензола и толуола при 82⁰С.

Расход теплоты, получаемой в кубе-испарителе от греющего пара, находим по уравнению:

Здесь тепловые потери приняты в размере 3% от полезно затрачиваемой теплоты; удельные теплоемкости взяты соответственно при , и ; температура кипения исходной смеси определена по рис. 7.6[7].

Расход теплоты в паровом подогревателе исходной смеси:

Здесь тепловые потери приняты в размере 5%, удельная теплоемкость исходной смеси взяты при средней температуре (91.5+18)/2≈55⁰С.

Расход теплоты, отдаваемой охлаждающей воде в водяном холодильнике дистиллята:

,

где удельная теплоемкость дистиллята взята при средней температуре (82+25)/2≈54⁰С.

Расход теплоты, отдаваемой охлаждающей воде в водяном холодильнике кубового остатка:

где удельная теплоемкость кубового остатка взята при средней температуре (109+25)/2=67⁰С.

Расход греющего пара, имеющего давление и влажность 5%:

а) в кубе-испарителе

где =2141×10³ Дж/кг – удельная теплота конденсации греющего пара;

б) в подогревателе исходной смеси

Всего: 0.84+0.23=1.07или 3,9.

Расход охлаждающей воды при нагреве ее на 20⁰С:

а) в дефлегматоре

б) в водяном холодильнике дистиллята

в) в водяном холодильнике кубового остатка

Всего: 0,0246или 89.

Заключение.

В процессе проделанной работы была рассчитана ректификационная установка для разделения смеси бензол-толуол.

Были получены следующие данные:

Диаметр колонны – 1970;

Высота колонны – 8.7;

Расход дистиллята - 5064;

Расход кубового остатка - 6936;

Расход Флегмового числа – 1.95;

Расход греющего пара:

а) в кубе-испарителе – 0.84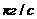

б) в подогревателе исходной смеси – 0.23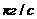

Всего: 1.07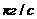или 3.9;

Расход охлаждающей воды:

а) в дефлегматоре – 0.0194;

б) в водяном холодильнике дистиллята – 0.00172;

в) в водяном холодильнике кубового остатка – 0.00344;

Всего: 0.0246или 89;

Скорость пара в колонне – 0.58;

Число тарелок:

Всего – 26, из них верхних - 12, нижних – 14;

С запасом: всего – 30, из них верхних – 14, нижних – 16.

4. Список используемой литературы.

1. Бушмелев В.А., Вольман Н.С. Процессы и аппараты целлюлозно-бумажного производства. Изд. 3-е. - М.: Лесная промышленность, 1974. - 352 с.

2. Касаткин А.Г. Основные процессы и аппараты химической технологии. Изд. 9-е. - М.: Химия, 1973. - 752 с.

3. Кувшинский М.Н., Соболева А.П. Курсовое проектирование по предмету “Процессы и аппараты химической промышленности”. - М.: Высшая школа, 1980.

4. Павлов К.Ф., Романков П.Г., Носков А.А. Примеры и задачипо  курсу процессов и аппаратов химической технологии. Изд. 10-е. - Л.: Химия, 1987. - 576 с.

5. Плановский А.Н., Рамм В.М., Каган С.З. Процессы и аппараты химической технологии. Изд. 4-е. - М.: Химия, 1968. - 848 с.

---

[1] Павлов К.Ф., Романков П.Г., Носков А.А. Примеры и задачи по курсу процессов и аппаратов химической технологии. Изд. 10-е. – Л.: Химия, 1987. – С. 283.

[2]Павлов К.Ф., Романков П.Г., Носков А.А. Примеры и задачи по курсу процессов и аппаратов химической технологии. Изд. 10-е. – Л.: Химия, 1987. – С. 327.

[3] Павлов К.Ф., Романков П.Г., Носков А.А. Примеры и задачи по курсу процессов и аппаратов химической технологии. Изд. 10-е. – Л.: Химия, 1987. – С. 327.

[4] Павлов К.Ф., Романков П.Г., Носков А.А. Примеры и задачи по курсу процессов и аппаратов химической технологии. Изд. 10-е. – Л.: Химия, 1987. – С. 323.

[5]Павлов К.Ф., Романков П.Г., Носков А.А. Примеры и задачи по курсу процессов и аппаратов химической технологии. Изд. 10-е. – Л.: Химия, 1987. – С. 323.

[6]Павлов К.Ф., Романков П.Г., Носков А.А. Примеры и задачи по курсу процессов и аппаратов химической технологии. Изд. 10-е. – Л.: Химия, 1987. – С. 324.

[7] Павлов К.Ф., Романков П.Г., Носков А.А. Примеры и задачи по курсу процессов и аппаратов химической технологии. Изд. 10-е. – Л.: Химия, 1987. – С. 327.