Зубчатые передачи

	Загрузить архив:
	Файл: ref-23934.zip (257kb [zip], Скачиваний: 448) скачать

Содержание

1. Общие сведенья о зубчатых передачах.
2. Геометрические и кинематические параметры зубчатых передач.

Цилиндрические зубчатые колеса

Конические зубчатые колеса

Червячные передачи

3. Краткая методика расчета цилиндрических зубчатых передач

      4.   Список литературы.

1. Общие сведенья о зубчатых передачах.

Глядя впервые на работающую зубчатую передачу возникает вопрос: как может равномерно вращаться зубчатая пара, если точка контакта сопряженных зубьев все время меняется, то ножка зуба одного колеса соприкасается с головкой другого, то наоборот?

А иногда в контакте одновременно находятся сразу две такиеточки, как например А1 и

А2 на рис 1. Ведь расстояния до центров колес О1и О2 у головок зубьев больше, чем ножек. Значит, и передаточные отношения в этих положениях разные?

Здесь следует твердо запомнить: зацепление зубчатых колес теоретически эквивалентно качению без скольжения друг по другу двух окружностей, называемых начальными. Следовательно, и передаточные отношение у зубчатых передач постоянно и не меняется от взаимного расположения зубьев( оговоримся только, что речь идет об обычных – круглых – зубчатых колесах; есть еще и не круглые , например эллиптические, зубчатые колеса где передаточное отношение циклически меняется при их вращении).

Для обеспечения постоянного передаточного отношения пары зубчатых колес их зубы должны быть очерчены по кривым, у которых общая нормаль, проведенная через точку касания профилей зубьев, всегда проходит через одну и ту же точку на линии, соединяющей центры зубчатых колес, называемую полюсом зацепления. Существует много кривых,  удовлетворяющих этому требования, но, наиболее подходящей по многим параметрам кривой, очерчивающей рабочий профиль зубьев, является эвольвента.

Эвольвента удовлетворяет основному закону зубчатого зацепления, согласно которому общая нормаль сопряженным профилям, проведенная в точке их касания, делит межосевые расстояние на части, обратно пропорциональные угловым скоростям.

Таким образом, для сохранения постоянства передаточного отношения, i=w1w2=const, точка П, называемая полюсом зацепления, должна сохранять на линии центров постоянное положение и делить межосевое расстояние а в отношении r2r1 рис 1.  

Рис.1 Схема двупарного зацепления.                   Рис. 2 Схема построения эвольвенты.

Эвольвентой называется кривая(рис.2), Описываемая любой точкой прямой, перекатывающейся без скольжения по неподвижной окружности. Если в первоначальный перекатывания окружности касается точка А0 прямой NN, то на различных этапах перекатывания точкаA0 будет занимать положения А1, А2, А3,…….., Аn. Прямая NN на этих же этапах будет касаться окружности в точках В1, В2, В3,……..,Вn. Длина окружности, которую проходит точка ее контакта с прямой NN – А0 В1, АоВ2,АоВ3,….., А0Вn, Всегда равна длине этой прямой от точки касания с окружностью, до точки Аi на прямой, описывающих эвольвенту - АоВ1= А1В1, АоВ2 = А2В2, АоВ3 = А3В3, …, АоВn = AnBn. Окружность диаметра db, по которой перекатывается прямая NN( производящая прямая), называется основной окружностью. Для построения профиля зуба используется часть полученной кривой – эвольвенты.

Схема передачи эвольвентного профиля представлена на рис. 3.

Рис. 3 Схема передачи с зубьями эвольвентного профиля: 1, 2- эвольвенты зубьев.

На этой схеме эвольвентный профиль зубьев построен следующим образом. О1и О2- оси вращения ведущего и ведомого колеса, соединенные линией О1О2 – линией центров.

вольном месте линии центров поставим точку, которую назовем полюсом зацепления П. Затем через точку П проведем линию ТТ, перпендикулярную линии центров, и из точек О, и О₂ построим окружности радиусами соответственно r_w]- ОДи /•„,] = О₂П, каса­ющиеся друг друга в точке П. Согласно сказанному выше, это и будут те окружности, которые своим качением друг по другу ими­тируют зубчатое зацепление. Эти окружности называются началь­ными. Межосевое расстояние a_wравно сумме радиусов начальных окружностей:

a_w = r_wl + r_w2.                                                    Рис.1

Затем под некоторым углом a_w— называемым углом зацепления (его стандартное значение для эвольвентного зацепления равно 20°, но встречаются углы зацепления больше и меньше этого зна­чения) к линии ТТ проводим прямую NN, называемую произво­дящей. Как было отмечено выше, перекатыванием этой произво­дящей прямой по некоторым чисто условным окружностям (ос­новным), получаем эвольвентный профиль зубьев. Чтобы постро­ить основные окружности, опустим из центров О, и О₂ перпенди­куляры на производящую прямую AWn точки пересечения Ки Lсоединим соответственно с центрами О₂ и О_х. Из центров О, и О₂ радиусами О,£ = r_blи О₂К = г_Ь2 проведем основные окружности, перекатыванием по которым линия NN образует эвольвенты 1 и 2.

Производящая прямая NN является общей нормалью к обеим эвольвентам 1 и 2 в точке касания с ними.

При вращении основных окружностей вместе со своими эволь­вентами точка касания этих эвольвент друг с другом перемещает­ся по прямой АХ, называемой линией зацепления.

Линия зацепления всегда проходит через одну и ту же точку П на линии центров О_{ О₂ — полюс зацепления, в котором началь­ные окружности касаются друг друга. Заметим, что при измене­нии межосевого расстояния a_wи начальные окружности изменят свои радиусы, подчиняясь условию (8.1).

Понятие начальной окружности для отдельно взятого зубчато­го колеса не имеет физического смысла, это понятие чисто кине­матическое. Однако при изменении межосевого расстояния и со­хранении прежнего значения передаточного отношения

/ = а>,/со₂ = r_w2/r_wl                                           Рис.2

радиусы начальных окружностей изменятся пропорционально зна­чению iи величину их можно найти из соотношений (1) и (2). Радиусы основных окружностей r_b]и г_Ь1 не изменятся, как не из­менятся и профили зубьев, очерченных прежними эвольвентами. Так как г_ьх = r_wlcosct*, и r_b2 = r_w2cosa^, то передаточное отноше­ние i - r_b2/r_b[. Следовательно, передаточное отношение, завися­щее от радиусов основных окружностей, которые не изменились с изменением a_lv, остается при этом постоянным.

Отсюда — важное следствие, что передаточное отношение эволь-вентного зацепления не нарушается с изменением межосевого расстоя­ния a_w. Отметим, что циклоидальное зацепление весьма чувствитель­но по своей кинематической точности к изменению a_w, что является его существенным недостатком по сравнению с эвольвентным.

Рабочие участки эвольвент, по которым зубья сопрягаются друг с другом, ограничены окружностями вершин зубьев. Участок ли­нии зацепления, заключенный между этими окружностями от точки В_х до точки В₂ (рис. 3), называется активной линией зацеп­ления. Если построить профили сопрягаемой пары зубьев в начале зацепления и в его конце (соответственно в точках В и В₂), то эти точки и определят те нижние точки зубьев на обоих колесах, ниже которых контакта зубьев не произойдет. Участок рабочей стороны профилей зубьев, ограниченный вершиной зуба и нижней точкой контакта, называется активным профилем зубьев (на рис. 3 эти активные профили зубьев заштрихованы).

Угол поворота зубчатого колеса от положения входа зуба в за­цепление до положения выхода из него, соответствующий, на­пример, дуге CDна начальной окружности ведомого колеса, на­зывается углом перекрытия зубчатого колеса передачи и обознача­ется ф   При этом центральный угол х (см. рис. 5), равный

т = 2тг/г,                                       Рис.3

где z — число зубьев колеса, называется угловым шагом зубьев. Отношение угла перекрытия зубчатого колеса передачи к его угловому шагу называется коэффициентом перекрытия и обозна­чается е_у:

е_у = _Фу/х.                                               Рис. 4

Для непрерывности зацепления необходимо, чтобы ф_т > т или е_у> 1, иначе одна пара зубьев выйдет из зацепления раньше, чем войдет другая, а этого допускать нельзя. Если 1 < г_т < 2, то период зацепления пары зубьев будет состоять из однопарного и двупарного зацеплений.

Чем больше коэффициент перекрытия, тем больше двупарный период и меньше однопарный. У обычных зубчатых колес в полю­се всегда однопарное зацепление. Между тем существуют методы создания зацепления, коэффициент перекрытия которого боль­ше двух. Это достигается некоторым удлинением зубьев и умень­шением угла зацепления, что повышает прочность и плавность работы передачи.

Представляет интерес зацепление зубчатого колеса с рейкой, изображенное на рис. 4. Данный случай зацепления особенно ва­жен для изготовления зубчатых колес, о чем будет сказано ниже.

Если вместо одного из зубчатых колес в зацеплении будет уча­ствовать рейка, то для оставшегося колеса будет всего одна окружность, катящаяся по начальной прямой рейки без скольже­ния. Эту окружность диаметром dбудем называть делительной, она как бы делится шагом рейки Р, на zравных частей (шаг рейки — это расстояние между одноименными сторонами двух соседних зубьев, взятое по средней линии).

Рис. 4. Зацепление зубчатого

колеса с рейкой:

1 — делительная окружность колеса;

2 — делительная прямая рейки

На делительной окружности шаг Р, и угол зацепления a_wнарезаемого колеса равны шагу и углу а профиля рейки. Если межосевое расстояние передачи точно равно сумме радиусов делительных окружностей обоих колес, то началь­ные и делительные окружности совпадают. На практике же иногда встречаются случаи, когда эти окружности отличаются, о чем бу­дет сказано ниже. Но для определения основных параметров зубча­той передачи принимается именно делительная окружность.

Отвечая на вопрос, заданный в самом начале этого подразде­ла, заметим, что передаточное отношение зубчатой передачи ос­тается постоянным, несмотря на различные радиусы точек кон­такта из-за того, что рабочие участки профилей зубьев одновременно и катятся, и скользят друг по другу. Только по радиусам начальных окружностей в полюсе зацепления имеет место чистое качение профилей друг по другу. Во всех остальных точках происходит ча­стичное скольжение рабочих поверхностей друг по другу тем боль­шее, чем больше расстояние от полюса. При этом важно, что точ­ки профилей головки имеют большую скорость, чем точки про­филей ножки, а следовательно, ножка зуба является отстающим звеном, она подвержена питтингу в первую очередь. Малые скорости скольжения в около­полюсной зоне также способствуют питтингу, поскольку коэф­фициент трения при малых скоростях скольжения велик. Поэтому основной зоной, подвергающейся питтингу на рабочем профиле, явля­ется ножка в околополюсной зоне.

Такое неравномерное изнашивание зуба имеет как отрица­тельные, так и положительные стороны. Отрицательная сторона ясна — искажается профиль зуба. А положительная состоит в воз­можности «приработки» зубьев друг к другу, о чем будет сказано ниже.

2. Геометрические и кинематические параметры зубчатых передач.

2.1. Цилиндрические зубчатые колеса.

Рассмотрим вначале наиболее простую цилиндрическую зуб­чатую передачу — прямозубую (рис. 5). Часть зубчатого колеса, на которой расположены зубья, называется венцом; часть, насажива­емая на вал, называется ступицей. Делительная окружность, име­ющая диаметр d, делит зуб по высоте на две части — головку вы­сотой h_aи ножку высотой hfiпри этом высота зуба h= h_a + h_f. Расстояние Р между одноименными профилями соседних зубьев, измеренное по дуге делительной окружности, называется окруж­ным делительным шагом зубьев; он складывается из окружной тол­щины зуба Sи ширины впадины е. Величина т, имеющая размер­ность длины и равная

т = Р/п, (Рис.5)

называется окружным делительным модулем, или просто модулем. Модуль — один из основных параметров зубчатого колеса; ко­леса, находящиеся в зацепле­нии друг с другом, должны иметь одинаковый модуль. Мо­дули стандартизованы, и их зна­чения можно узнать из части 5 учебника. В машиностроении чаще всего используются зна­чения модулей от 1 до 14 мм.

Все основные параметры зуб­чатых колес выражают через мо­дуль. Шаг зубьев Р = пт; диа­метр делительной окружности

d = mz,

(Рис.5)

Рис. 5. Цилиндрическое зубчатоеколесо с прямыми зубьями:

1 — окружность вершин зубьев; 2 — делительная окружность; 3 — окруж­ность впадин

где z — число зубьев того коле­са, делительную окружность ко­торого определяют.

При изготовлении зубчатых колес в качестве исходного рас­сматривается зацепление коле-

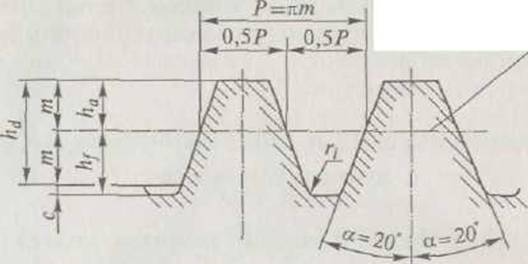
са с зубчатой рейкой. При этом рейка называется номинальной ис­ходной зубчатой рейкой, и контур ее зубьев называют исходным контуром. В соответствии со стандартным исходным контуром для цилиндрических зубчатых колес (рис. 6) высота головки зуба h_a= = т, высота ножки зуба h/ = m + c = 1,25m, где с — радиальный зазор; профиль исходного контура в пределах глубины захода h_d ~ = 2т прямолинейный; у основания зуба имеется радиус закругле­ния г, = 0,25т. Исходя из сказанного: высота зубьев цилиндрических колес

Рис. 6. Стандартный исходный контур для цилиндрических зубчатых колес

                                                             =2,25m;                      (Рис.6)

диаметр вершин зубьев

                                               d_a = d + 2h_a = mz-i    = m(z          (Рис.7)

диаметр впадин

                                              d_f=d-2h_f =mz-2-                          (Рис.8)

Межосевое делительное расстояние зубчатой передачи

                                                                                                    (Рис.9)

Знак «-» соответствует внутреннему зацеплению. Если межосе­вое расстояние отличается от делительного, что также встречает­ся, то обозначается a_w.

Расстояние между торцами зубьев Ъ (длина зуба) называется шириной венца (рис. 8.5). В процессе работы прямозубой передачи пара зубьев входит в зацепление сразу по всей длине контакта (теоретически контакт зубьев происходит по линии), что сопро­вождается ударом зубьев друг по другу. Но так как другая пара зубьев, которая уже находилась в зацеплении, еще не вышла из него, в зацеплении находятся две пары зубьев. Затем также одно­моментно эта другая пара выходит из зацепления, и в контакте остается только одна пара зубьев. Все это сопровождается измене­ниями в деформациях зубьев, которые при однопарном зацеплении сильнее, чем при двупарном, вибрациями и другими дина­мическими нагрузками. Как было уже сказано, продолжительность нахождения передачи в одно- и двупарном зацеплениях зависит _оТ коэффициента перекрытия е.

Прямозубая передача имеет только торцовое перекрытие. Коэф­фициент торцового перекрытия е_а (отличается от коэффициента перекрытия е_у индексом) равен отношению угла торцового пере­крытия ф_а к угловому шагу т:

£«=Ф_а/т.                                    (Рис.10)

Для прямозубых передач ср_а соответствует (p_Y на рис. 8.3, а ко­эффициент торцового перекрытия для этих передач рекомендует­ся принимать е_и > 1,2.

Стандартом предусмотрено 12 степеней точности для цилинд­рических зубчатых колес, причем первая — наивысшая. Для каж­дой степени точности установлены нормы кинематической точ­ности, плавности работы и контакта зубьев и передач. В машино­строении передачи общего назначения изготовляют по 6—9-й сте­пеням точности, которые применяют для прямозубых колес при окружных скоростях до 15...2 м/с соответственно.

Наиболее распространены в машиностроении косозубые зубча­тые колеса (рис.7). Косозубые передачи с параллельными осями имеют противоположное направление зубьев ведущего и ведомого колес (рис. 7, а) и так же, как и прямозубые, относятся к цилиндри­ческим зубчатым передачам. Отметим для сравнения, что винто-колесные передачи (см. рис. 2.12), оси которых скрещиваются и колеса которых похожи на косозубые, имеют одинаковые направ-

Рис.7. Параметры цилиндрических косозубых зубчатых колес и пере­дач: а — направление зубьев; б — сечение зубьев нормалью

ления зубьев обоих колес; исходный контакт рабочих поверхнос­тей зубьев у них происходит не по линии, а в точке.

Если представить себе линию пересечения боковой поверхнос­ти зуба косозубого колеса с делительной цилиндрической повер­хностью, то получится винтовая линия постоянного шага. В косо­зубых колесах эта линия (линия зуба) может иметь правое и левое направление, как винтовая линия резьбы. Угол наклона линии зуба обозначается буквой р.

Как видно из рис. 7, а, у косозубых передач контактные ли­нии расположены наклонно по отношению к линии зуба, поэто­му в отличие от прямых зубьев косые входят в зацепление не сра­зу по всей длине, а постепенно. Угол перекрытия косозубого ко­леса состоит из торцового и осевого углов перекрытия, и коэф­фициент перекрытия е_т косозубой передачи складывается из ко­эффициентов торцового е_а и осевого е_р перекрытий:

е_г =£« +е_р > 2.                                (8.Ц)

В отличие от прямозубой передачи у косозубой нет периода од-попарного зацепления. Поэтому эти передачи отличаются существен­но большей прочностью и плавностью работы. Например, для косозубых колес 6—9-й степеней точности допустимы окружные скорости 30...4 м/с соответственно.

Так как косозубые колеса обрабатываются теми же зуборезны­ми инструментами, что и прямозубые, стандартные параметры колес задаются в нормальном сечении NN к зубу (рис. 8.7, б). Для косозубых колес используются три модуля: нормальный — т„ = Р„/п, окружной — т, = Р,/п и осевой — т_х = Р_х/п, где Р„, Р, и Р_х — соответственно нормальный шаг, измеренный по делительной ок­ружности; окружной шаг, измеренный по дуге делительной ок­ружности в торцовом сечении; осевой шаг, измеренный по обра­зующей делительного цилиндра.

Как следует из рис. 7, б:

Р, =Р„/соБр; т, =m_fl/cosp.                    

Все размеры зубьев косозубого колеса определяют по нормаль­ному модулю т_п:

h = ha + h_f = т_п + 1,25т„ = 2,25т„,                  

а диаметр делительной окружности — по окружному модулю:

d = m,z- m_nz/cosp.                            (8. И)

Другие размеры косозубых колес определяют по формулам:

диаметр вершин зубьев

d_a =d + 2h_a =d + 2m_n;                             

диаметр впадин

d_f =d-2h_f =d-2,5m_n;                     

межосевое расстояние

a = m,{z + Z₂)/2 = m_ri(z_l + ^₂)/(2cosp).             

Коэффициент осевого перекрытия косозубой передачи

где Ь — ширина венца; Р_х — осевой шаг.

Если ер — целое число, то суммарная длина контактных линий будет все время оставаться постоянной, что положительно отра­жается на работе передачи, так как нагрузка на зубья в процессе зацепления остается постоянной (для сравнения см. сказанное выше о нагрузках на зубья прямозубых колес).

Суммарная длина контактных линий косозубой передачи

1_г = £e_a/cosp.                               

Недостатком косозубых передач можно считать возникающую при работе передачи осевую силу F_a, вызванную углом р и равную

F_a = Ft*b                                 

где F; = 2Tjd, здесь Т — передаваемый вращающий момент, d— диаметр делительной окружности.

Этот недостаток устраняется в шевронных зубчатых колесах, венец которых по ширине состоит из участков с зубьями с проти­воположными углами наклона (рис.8).

В шевронных колесах осевые силы F_aвзаимно уравновешива­ются и на опоры валов не передаются. На рис. .8, а показано шевронное зубчатое колесо с дорожкой шириной а посреди вен­ца; так технологичнее нарезать зубья фрезой, но колесо получается

Рис.8. Цилиндрическое шевронное зубчатое колесо: а — с дорожкой посередине колеса; б — без дорожки

большой толщины. На рис. 8, £ представлено шевронное ко­лесо без дорожки, изготовление которого затруднительно.

Так как осевые усилия в шевронных колесах уравновешены углы наклона зубьев р могут быть увеличены от 20°, наибольшей их величины для косозубых колес в общем машиностроении, до 40... 45°. При этом плавность работы и ее нагрузочная способность существенно возрастают. Однако шевронные колеса трудоемки в изготовлении и дороги, требуют специфической фиксации в опо­рах. В осевом направлении закрепляется только одно колесо, а сопрягаемое с ним второе колесо должно свободно передвигаться в этом направлении, так как осевая фиксация здесь происходит по зубьям шевронного колеса.

Геометрические, кинематические и прочностные расчеты шев­ронной передачи аналогичны косозубым.

Зубчатые передани с зацеплением М.Л. Новикова были упомяну­ты в п. 2.2.1. Рассмотрим их основные геометрические и кинемати­ческие параметры.

Основным отличием зацепления М.Л. Новикова от эвольвент-ного является то, что зубья контактируют друг с другом по на­чальному контакту в точке, причем выпуклая поверхность одного зуба сопрягается с вогнутой поверхностью другого.

Такой выпукло-вогнутый контакт — самый выгодный с точки зрения минимизации возникающих контактных напряжений. Как видно из рис. .9, разница между радиусами кривизны выпуклого зуба шестерни г, и вогнутого зуба колеса г₂ (так чаще всего выпол­няют передачи Новикова) невелика. Именно это дает резкое сни­жение контактных напряжений. На рис. 8.9 профили зубьев пока­заны в нормальном сечении. Видно, что эти профили, очерченные дугами окружностей, не удовлетворяют основному принципу зацеп­ления — точка контакта А будет перемещаться не по общей нормали, как в эвольвентном зацеплении, а вдоль зубьев (от одного торна к другому), которые выполнены косыми, и их боковые по­верхности имеют весьма большие радиусы кривизны р, и р₂ вин­товых линий (см. рис. 9). Скорость перемещения точки контакта превышает окружную скорость колеса раза в три, что создает хо­рошие условия для смазки. Таким образом, при вращении колес косые зубья перекатываются друг по другу в плоскости NN. Поэтому торцовое перекрытие и геометрическое скольжение зубьев в переда­че Новикова теоретически отсутствуют.

Рис.9. Схема передачи с зацеплением М.Л.Новикова

Первое требует для плав­ности работы обязательно осевого перекрытия больше единицы _е > 1,1, что обеспечивается косыми зубьями с р^ 10...24°. Отсут­ствие геометрического скольжения прежде всего повышает КПД передачи Новикова по сравнению с эвольвентными передачами, а также устойчивость к питтингу.

Различают передачи Новикова с одной и с двумя линиями зацеп­ления. В последнем случае профиль зубьев обоих колес выпукло-вог­нутый. Передачи с двумя линиями зацепления (рис. 10), проходя­щими через две точки контакта предпочтительнее передач с одной линией зацепления. Во-первых, они прочнее, как на контактную прочность, так и на изгиб, что особенно важно для данного типа передач. Во-вторых, зубья таких передач могут нарезаться одним инструментом, так как у них один исходный контур.

Следует отметить, что с зацеплением Новикова нарезают не только цилиндрические, но и конические передачи.

Подытоживая сказанное, можно констатировать, что переда­чи Новикова, по сравнению с эвольвентными, прочнее по кон­тактной прочности в 1,5... 1,7 раза, имеют на 25...30% меньшие габаритные размеры, более экономичны по КПД и менее чув­ствительны к перекосам осей. Недостатками этих передач являют­ся прежде всего сложность инструмента, некоторое снижение изломной прочности (выламываются края зубьев близ торцов) и

Р=пт

Рис. 10. Исходный контур передачи М.Л.Новикова с двумя линиями

контакта: 1 — полюс; 2 — точки контакта

Рис. 11. Расположение пятен кон­такта (заштрихованы) на рабочих поверхностях зубьев зацепления М. Л. Новикова

чувствительность к изменению межосевого расстояния. Последнее в частности, ограничивает применение зацепления Новикова в коробках передач автомобилей.

Исходный контур передачи Новикова с двумя линиями контакта представлен на рис. 10, где основные геометрические параметры выражены через модуль т с соответствующими коэффициентами:

К = 0,9; с = 0,15; _Ра = 1,15; _Р/= 1,25.              

Основные геометрические размеры зубчатых колес с зацепле­нием Новикова (с двумя линиями зацепления)

d = m,z; d_a = d + 2m_nh_a; d_f = d - 2m_n (h_a + c); a = 0,5m_t(z_] +z₂); Щ= m«/cosp; a = 27°.            

Обозначения здесь те же, что и для эвольвентных передач.

Стандарт на расчет геометрии зацепления Новикова с двумя линиями зацепления ограничивает твердость зубьев Н < 320 НВ, модуль т < 16 мм, окружную скорость V< 20 м/с.

Интересно расположение пятен контакта на рабочих поверхно­стях зубьев зацепления Новикова (рис. 11). Они имеют сложную форму, близкую к треугольной или трапецеидальной, и находятся на линиях зацепления (в передачах с двумя линиями зацепления — на обеих), перемещаясь при работе передачи вдоль длины зуба. Видно, что точечный исходный контакт этого зацепления из-за выпукло-вогнутого контакта и больших радиусов кривизны винто­вых линий переходит в достаточно большие площадки. Контактные напряжения при таких больших площадях контакта, с одной сто­роны, очень малы, а с другой — они уже определяются не вполне по формулам Герца, а сходны с напряжениями смятия. Все это усложняет расчет на прочность зубьев с зацеплением Новикова.

2.2 Конические зубчатые колеса

О зубчатых передачах с коническими колесами уже вкратце было сказано. Отметим, что оси конических колес пересе­каются, причем чаще всего под углом £ = 90°. Зубья конических колес бывают, как правило, пря­мые и круговые; реже — шеврон­ные. Прямые зубья конических колес зацепляются между собой _с исходным контактом по линии, дуговые — в точке. Конические колеса с круговым зубом более прочны, чем прямозубые, плав­нее работают. Сопряженные ко­леса с круговым зубом имеют противоположное направление линии зубьев, шестерни обыч­но — правое, колеса — левое, если смотреть со стороны вер­шин конусов.

Стандартом установлено 12 степеней точности конических колес. Максимальные окружные скорости прямозубых колес для 6—9-й степеней точности соот­ветственно 12... 1,5 м/с; для колес с круговым зубом соответственно 20... 3 м/с.

На рис. 8.12 представлена схема геометрии зацепления кони­ческих колес. Вместо начальных и делительных цилиндров в кони­ческих передачах используются начальные и делительные конусы. Начальные конусы, как и начальные цилиндры в цилиндричес­ких передачах, катятся друг по другу без скольжения. В конических передачах начальные и делительные конусы всегда совпадают. Угол I между осями зубчатых колес равен сумме углов делительных конусов S = 5! +8₂.

Профилировка зубьев конических колес осуществляется на раз­вертке дополнительного конуса, образующая которого перпенди­кулярна образующей делительного конуса. Используют дополни­тельные конусы для внешнего, внутреннего и среднего сечений конического колеса, причем ширина венца Ь ограничена внешним и внутренним дополнительными конусами (см. схему рис. 12).

Зубья конических колес выполняют трех осевых форм. Форма 1 — нормально понижающиеся зубья (рис. 13, а), когда они рав­номерно уменьшаются по модулю по направлению к центру. При­меняется для прямых зубьев и при малых модулях для круговых зубьев. Форма 2 — равноширокие зубья (рис. 13, б), т.е. такие, у которых ширина впадины между зубьями постоянна по длине, но толщина самого зуба растет с увеличением расстояния от верши­ны. Эта форма наиболее распространена для колес с круговыми ³Убьями и применяется в массовом производстве, так как имеет Технологические преимущества (одним инструментом можно об-

Рис. 12. Схема геометрии зацеп­ления конических колес

Рис. 13. Осевые формы конических зубчатых колес:

а — нормально понижающиеся зубья; 6 — равноширокие зубья; в — равновы-

сокие зубья

работать сразу обе поверхности зубьев). Форма 3 — равновысокие зубья (рис. 13, в), где их высота постоянна по всей длине. Приме­няют для круговых зубьев при большом их числе.

Далее рассматриваются только равнопонижающиеся зубья.

Размеры конических колес обычно определяют по внешнему торцу зуба, образованному внешним дополнительным конусом. Внешний окружной модуль т_е для прямозубых колес и т_{е — для колес с круговым зубом имеет место на внешнем торце колеса. Этот модуль обычно не округляют до стандартного.

Передаточное отношение коничес­кой передачи (см. рис. 12)

co₂ = =d_e2jd_eX =

где d_eX, d_e2— внешние делительные диа­метры конусов шестерни и колеса.

Для конической прямозубой переда­чи передаточное отношение стараются не принимать выше трех, а для колес с круговыми зубьями — выше 6,3.

У конического колеса с круговыми зубьями угол наклона зубьев р„ измеря­ется в середине ширины зубчатого вен­ца на окружности среднего диаметра ко-

Рис. 14. Схема коническо­го зубчатого колеса с кру­говыми зубьями

леса d_m(рис. 8.14), обычно принимают р„ = 35°. Круговой зуб распо­лагается по дуге окружности а, что дает возможность нарезания зу­бьев резцовыми головками

Ширину зубчатого венца b(см. рис. .12) рекомендуется при­нимать

Ь<10т_е.                                    

Основные геометрические соотношения для прямозубых ко­нических колес и для колес с круговым зубом с р„ = 35° (рис. .12 — .14) приведем для простоты без использования модификации зубьев (см. ниже) и обозначая внешний окружной модуль для обоих типов колес буквой т без индексов:

внешний делительный диаметр

d_ei =mzud_e2 = внешнее конусное расстояние

модуль нормальный в среднем сечении:

для прямозубых колес

т„ « 0,857т;

для колес с круговым зубом

т_п % 0,702т;

высота головки зуба внешняя

h_ae = m;

высота ножки зуба внешняя

h_fe= 1,2т;

угол ножки зуба

t£Q_f=h_fe/R_e;

угол головки зуба

Gei=0/2! б<з» =0/i-

Остальные параметры несложно получить геометрическим рас­четом по рис. 12 и 13.

2.3. Червячные передачи

Учитывая, что основными видами передач со скрещивающимися осями, преобладающе распрос траненными в общем машиностроении, являются червячные данном курсе подробно рассмотрим именно их. Гипоидные передачи, имеющие преимущественное распространение в автомоби­лях, подробно рассматриваются, например, в курсе «Конструи­рование и расчет автомобиля». Винтоколесные передачи мало рас­пространены в машиностроении; к тому же они представляют собой частный случай червячных передач.

Червячные передачи — это зубчато-винтовые передачи, движе­ние в которых осуществляется по принципу винтовых передач сколь­жения. Угол между проекциями на параллельную плоскость скре­щивающихся осей червячных передач обычно составляет 90°.

В червячной передаче, как и в зубчатой, присутствуют диамет­ры начальных и делительных цилиндров (рис. 15): d_wlи d_x— начальный и делительный диаметры червяка; d_w2и d₂ — началь­ный и делительный диаметры колеса. Если передача без модифи­кации зубьев, то d_wX = diи d_w2 = d₂. Точка касания начальных ци­линдров является полюсом зацепления.

В отличие от зубчатых колес, которые практически эквивален­тны друг другу, в червячных передачах червяк и червячное колесо существенно отличаются друг от друга.

Червяки различают по форме поверхности, на которой обра­зуется резьба, на цилиндрические и глобоидные; по форме профи­ля резьбы в осевом сечении на прямолинейный и криволинейный профили. Наиболее распространены цилиндрические червяки с прямолинейным профилем в осевом сечении. В торцовом сече­нии витки такого червяка образуют архимедову спираль, отсюда и название — архимедов червяк.

Рис. 15. Схема червячной передачи

Рис. 16. Формы профиля резьбы червяка в осевом сечении: а — прямолинейная; б — криволинейная

Однако для шлифования архимедовых червяков требуются спе­циальные шлифовальные круги с криволинейным профилем, что усложняет обработку. Шлифование червяков с высокой твердо­стью поверхности при #> 45 HRC существенно увеличивает дол­говечность передачи, так как в противном случае шероховатый червяк как напильником сточит рабочий профиль червячного ко­леса. Поэтому для червяков из высокотвердых шлифованных ста­лей используют эвольвентный профиль резьбы. Такие эвольвентные червяки подобны эвольвентным косозубым колесам с очень ма­лым числом зубьев, равным числу заходов резьбы червяка, а ста­ло быть, с очень высоким значением угла р. Это дает возможность шлифования эвольвентных витков червяка плоской стороной шли­фовального круга на червячно-шлифовальных станках.

Методы нарезания элементов червячной передачи будут рас­смотрены в этой главе позже, но скажем только, что при одина­ковом качестве изготовления форма профиля резьбы мало влияет на несущую способность и долговечность передачи.

На рис. 16 представлен червяк с прямолинейным (а) и кри­волинейным (б) профилем резьбы в осевом сечении. Угол а на рис. 8.16 — профильный угол сс= 20°; Р = пт — шаг резьбы, т — осевой модуль. Резьба червяка может быть однозаходной (z, = 1 при / > 30) или многозаходной (z = 2 при / = 15...30; Z = 4 при ' = 8... 15).

Делительный диаметр d_xчервяка связан с модулем т коэффи­циентом диаметра червяка q

g = d_x/m.                                      

Значения дит стандартизованы. Чаще всего # = 8; 10; 12,5; 16; 4), а щ = 2; 2,5; 3,15; 4; 5; 6,3; 8; 10; 12,5 мм. Рекомендуется коэф-

Рис. 17. Сечение червяка и колеса плоскостью, перпендикулярной оси червяка

фициент диаметра q>0,25г₂, где z₂ колеса.

Угол подъема винтовой линии

tgy =nmz_l/(nd_l) = m_Zxjd_x= zjq. Диаметры (рис. 16)

d_y = qm; d_al*d_x+ 2m; d_fl= d_{ -2,4m.

число зубьев червячного.                    

Длина нарезаемой части червяка Ъ_х (см. рис. 16) определяется так, чтобы одновременно входило в зацепление наибольшее чис­ло зубьев колеса. При отсутствии модификации зубьев:

для одно- и двухзаходных червяков

для четырехзаходных червяков

Для червячных колес без модификации зубьев (рис. 17) d₂= z₂m; d_a2 =d₂ + 2m; d_f2 =d₂- 2,Am; a_w=0,5(q + z₂)mМинимальное число зубьев из условия их неподрезания

Z₂ > 28.                                     

Диаметр колеса d_aM2и его толщина Ь₂ при угле обхвата червя­ка колесом 28 «100° и однозаходном червяке равны соответствен­но d_aM2 a₂+2m, ^^0,754,, при четырехзаходном червяке d_aM2 ^d_a2+m,Z>2 < 0,67d_al.

Стандартом установлены 12 степеней точности червячных пере­дач. Основы этого стандарта такие же, как и для других зубчатых передач. Например, для 7-й степени точности скорость скольжения < 10 м/с; для 8-й — V_s < 5 м/с; для 9-й степени V_s < 2 м/с. ^S Скорость скольжения V_sнаправлена по касательной к винто­вой линии червяка. Она равна _где К, =710^1/60; V₂ = nd₂n₂/60;V₂/V_l=tgy.

Так как угол подъема винтовой линии у обычно невелик, то V₂ всегда меньше К_ь aV_sбольше V_x.

Передаточное отношение червячной передачи не может быть выражено отношением d₂/d_uкак в других зубчатых передачах, так как окружные скорости V_xи V₂перпендикулярны друг другу. При одном обороте червяка колесо поворачивается на угол, охва­тывающий число зубьев, равное числу заходов червяка. Для пово­рота червячного колеса на один оборот необходимо, чтобы чер­вяк сделал z₂fzоборотов. Отсюда передаточное отношение чер­вячной передачи

i = _nJn₂=z₂/z_lТак как Zдля червяка очень мало (z= 1 — 4), то / может быть достаточно велико. В червячной передаче можно реализовать боль­шие передаточные отношения в одной паре, что является достоин­ством червячных передач.

В силовых червячных передачах обычно / = 10...60. Ведущим чаще всего является червяк, но при числе заходов Z= 2, а осо­бенно Z= 4 ведущим может быть и червячное колесо, хотя и с меньшим КПД передачи, чем при ведущем червяке. При ведущем колесе червячная передача является сильно повышающей.

3.Краткая методика расчета цилиндрических зубчатых передач

Выбор материала. Основным материалом для изготовления зубчатых колес служат углеродистые и легированные стали. Ус­ловно все передачи в зависимости от твердости разделены на при­рабатывающиеся (с твердостью Н < 350 НВ) и неприрабатываю-щиеся (с твердостью Н > 350 НВ).

В табл. 20.3 представлены"механические характеристики и тер­мообработка некоторых марок сталей, которые наиболее часто

Механические характеристики и термообработка

некоторых марок сталей, используемых при изготовлении прирабатывающихся зубчатых колес и других деталей машин

Марка стали	ав, МПа	а , МПа	Твердость рабочих поверхно­стей зубьев, НВ	Термообработка
35	500... 600 700... 800 800... 900	250 400 550	140... 170 194...222 223...250	Нормализация Закалка 860 °С, вода + отпуск 600 °С Закалка 860 °С, вода + отпуск 500 °С
35Л	500... 600	270	163...207	Нормализация
40	500... 600 700... 800	280 400	152...207 192...228	Нормализация Закалка 860 °С, вода + отпуск 550 °С
40Л	530	300	153...196	Закалка 870 °С, вода + отпуск 600 °С
45	600... 700 700... 800 800... 900	320 400 550	167... 194 194...222 223...250	Закалка 860 °С, вода + отпуск 600 °С Закалка 860 °С, вода + отпуск 400 °С Нормализация
45Л	500... 600 600... 700	270 410	160...212 207...235	Нормализация Закалка 860 °С, вода + отпуск 600 °С
50	640 700... 900	350 530	179...228 228...255	Закалка 840 °С, вода + отпуск 600 °С Закалка 860 °С, вода + отпуск 400 °С
35Х	700... 750	490	220...260	Закалка 860 °С, масло + отпуск 600 °С
35ХМ	700... 800 900...950	670 790	235...262 269...302	Закалка 860 °С, вода + отпуск 600 °С Закалка 860 °С, вода + отпуск 500 °С
35ХГСА	970 1100	810 1000	280 320	Закалка 880 °С, масло + отпуск 600 °С Закалка 880 °С, масло + отпуск 500 °С
40Х	700... 800 800... 900 900... 1000	400 550 700	200...230 230...257 257...287	Закалка 860 °С, масло + отпуск650°С Закалка 860 °С, масло + отпуск 600 °С Закалка 860 °С, масло + отпуск 500 °С
45Х	800... 900	650	240...280	Закалка 850 °С, масло + отпуск 500 °С
40ХН	800... 900 900... 1000	550 700	215...243 265...295	Нормализация Закалка 790 °С, масло + отпуск 540 °С

Список литературы:

1. «Детали машин» Н.В. Гула, В.Г. Клоков, С.А. Юрков Москва 2004 год
2. «Техническая механика» И.В. Аничкин, А.А. Эрдеди Москва 1980 год