Разложение рациональной дроби на простейшие.
| Примечание | от автора: Требует некоторого редактирования |
| Загрузить архив: | |
| Файл: ref-23994.zip (117kb [zip], Скачиваний: 166) скачать |
Федеральное агентство по образованию
Государственное общеобразовательное учреждение
высшего профессионального образования
Башкирский Государственный Университет
Нефтекамский филиал
Кафедра МиПОВМ
Курсовая работа
Тема: Разложение рациональной дроби на простейшие.
Выполнил студент
группы М-31
Остапов А. Б.
Принял:
Вильданов А. Н.
Нефтекамск 2006
Содержание.
· Введение.
· Часть 1. “Теоретическая часть к курсовой работе”.
· Часть 2. “Практическая часть к курсовой работе”.
o § “Реализация метода простых коэффициентов в Maple”.
o § “Реализация метода простых коэффициентов на Delphi”.
· Заключение.
· Список литературы.
Введение.
Этот вопрос уже много раз изучен и рассмотрен. Казалось бы, что может быть проще для современного математика, чем разложить рациональную дробь на простейшие, разве что элементарные алгебраические операции. Однако, применение этого метода существенно облегчает жизнь – не будь метода – некоторые задачи было бы очень проблематично решить, а некоторые вообще не решались.
Основные операции, в которых я применял этот метод, были:
а) Разложение рациональной дроби на простейшие с целью дальнейшего интегрирования получившихся элементарных дробей (Матем. анализ);
б) Разложение рациональной дроби на простейшие для использования в процессе преобразования Лапласа, что иногда серьезно ускоряет нахождение решения различных уравнений и систем уравнений в частных производных (Курс уравнений мат. физики).
Разложение – это необходимость. Без нее нельзя обходиться, тем более на современном этапе развития математической мысли. Об этом и пойдет речь в моей курсовой работе.
Часть 1.
“Теоретическая часть к курсовой работе”.
Рациональной дробью назовем отношение двух алгебраических многочленов с вещественными коэффициентами:

Дробь называется правильной, если степень P(x) меньше степени Q(x), и неправильной в противном случае. Простейшей называется правильная дробь, знаменатель которой представляет собой неприводимый (значит не имеющий корней) над некоторым полем (в нашем случае — поле действительных чисел) многочлен.
Для простых (правильных) дробей с действительными коэффициентами справедлива следующая теорема о разложении на сумму простейших:
Пусть (1) — правильная рациональная дробь с действительными коэффициентами, знаменатель которой имеет вид:

тогда для этой дроби справедливо следующее разложение на сумму простейших
дробей:
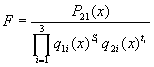
где индексированные переменные B, M, N — некоторые вещественные постоянные (может быть, равные нулю).
Для определения конкретных значений сих коэффициентов следует привести равенство к общему знаменателю и сравнить коэффициенты при одинаковых степенях x в числителе. Т.е. по сути дела решить систему линейных уравнений. Используется эта конструкция по большей части при вычислении интегралов, т.к. таким образом интеграл произвольной рациональной функции сводится, по сути дела, к сумме табличных интегралов.
Рациональной дробью R(x) называется дробь, числителем и знаменателем которой являются многочлены, т. Е. всякая дробь вида:
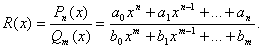
Если степень многочлена в числителе больше или равна степени многочлена в знаменателе (n≥m), то дробь называется неправильной. Если степень многочлена в числителе меньше степени многочлена в знаменателе (n≤m), то дробь называется правильной.
Всякую неправильную рациональную дробь можно представить в виде суммы многочлена (целой части) и правильной рациональной дроби (это представление достигается путем деления числителя на знаменатель по правилу деления многочленов):

где R(x) –
многочлен-частное (целая часть) дроби  Pn(x) – остаток
(многочлен степени n < m).
Pn(x) – остаток
(многочлен степени n < m).
Интегрирование простейших дробей. Простейшей дробью называется правильная рациональная дробь одного из следующих четырех типов:
1) 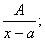
2)  (n≥2);
(n≥2);
3) 
4)  (n≥2).
(n≥2).
Здесь А, a, p, q, M, N – действительные числа, а трехчлен не имеет действительных корней, т. е. p2/4-q < 0.
Простейшие дроби первого и второго типов интегрируются непосредственно с помощью основных правил интегрального исчисления:

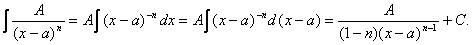
Интеграл от простейшей дроби третьего типа приводится к табличным интегралам путем выделения в числителе дифференциала знаменателя и приведения знаменателя к сумме квадратов:



Интегрирование рациональных дробей.
Разложение
рациональной дроби на простейшие дроби. Всякую правильную рациональную дробь  можно представить в
виде суммы конечного числа простейших рациональных дробей первого – четвертого
типов. Для разложения
можно представить в
виде суммы конечного числа простейших рациональных дробей первого – четвертого
типов. Для разложения  на простейшие дроби
необходимо разложить знаменатель Qm(x) на
линейные и квадратные множители, для чего надо решить уравнение:
на простейшие дроби
необходимо разложить знаменатель Qm(x) на
линейные и квадратные множители, для чего надо решить уравнение:
 - (5)
- (5)
Теорема. Правильную рациональную дробь  где
где  можно единственным
образом разложить на сумму простейших дробей:
можно единственным
образом разложить на сумму простейших дробей:

 - (6)
- (6)
(A1, A2, …, Ak, B1, B2, …, B1, M1, N1, M2, M2, …, Ms, Ns – некоторые действительные числа).
Метод
неопределенных коэффициентов. Суть
метода неопределенных коэффициентов состоит в следующем. Пусть дано разложение
правильной рациональной дроби  по формуле (6) на
простейшие дроби с неопределенными коэффициентами. Приведем простейшие дроби к
общему знаменателю Qm(x) и приравняем
многочлен, получившийся в числителе, многочлену Pn(x).
по формуле (6) на
простейшие дроби с неопределенными коэффициентами. Приведем простейшие дроби к
общему знаменателю Qm(x) и приравняем
многочлен, получившийся в числителе, многочлену Pn(x).
Метод
частных значений. При нахождении
неопределенных коэффициентов вместо того, чтобы сравнивать коэффициенты при
одинаковых степенях х, можно дать
переменной х несколько частных
значений (по числу неопределенных коэффициентов) и получить таким образом
систему уравнений относительно неопределенных коэффициентов. Особенно выгодно
применять этот метод в случае, корни знаменателя рациональной дроби  просты и
действительны. Тогда оказывается удобным последовательно полагать равным
каждому из корней знаменателя.
просты и
действительны. Тогда оказывается удобным последовательно полагать равным
каждому из корней знаменателя.
Правило интегрирования рациональных дробей. Для того чтобы проинтегрировать рациональную дробь, необходимо выполнить следующие действия:
1)
если рассматриваемая рациональная дробь  - неправильная (k≥m),
представить ее в виде суммы многочлена и правильной рациональной дроби:
- неправильная (k≥m),
представить ее в виде суммы многочлена и правильной рациональной дроби:
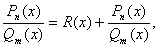
где n < m; R(x) – многочлен;
2)
если рассматриваемая рациональная дробь  - правильная (n < m),
представить ее в виде суммы простейших рациональных дробей по формуле (6);
- правильная (n < m),
представить ее в виде суммы простейших рациональных дробей по формуле (6);
3) интеграл от рациональной дроби представить в виде суммы интегралов от целой части и от соответствующих простейших дробей и вычислить эти интегралы.
Интегрирование дробно-рациональных функций.
Пусть  и
и  некоторые полиномы степени m и n
некоторые полиномы степени m и n


Функция вида
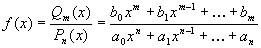
называется дробно-рациональной функцией , или коротко-рациональной дробью.
При m Интегралы от дробно –рациональных функций всегда
вычисляются. Однако мы не будем рассматривать полную теорию интегрирования
таких функций , а рассмотрим только два наиболее важных частных случая Случай 1 Подынтегральная функция имеет вид где все Основной результат который мы приведём без
доказательства , утверждает , что f(x) в этом случае можно представить в виде: Слагаемые вида Рассмотрим вопрос о нахождении
коэффициентов а) Умножим обе части разложения на
простейшие на б) И положим x=b1 . Так как при этом
(x-b1)=0 , то получи (символ Аналогично можно найти и все остальные а) в выражении для f(x) вычеркнуть
сомножитель б) в оставшемся выражении положить Если все Пример: Вычислить а) Разложим подынтегральную функцию на
простейшие. Имеем Поэтому б)Интегрируем Случай 2. Подынтегральная функция
имеет вид Если теперь найти все коэффициенты Bij, то метод разложения приведёт к интегралам 1
и 2 типов которые легко вычисляются. Для нахождения коэффициентов Bijможно использовать так
называемый метод неопределённых коэффициентов. Его алгоритм следующий. а) пишут разложение рациональной дроби на
простейшие с неопределёнными коэффициентами ; б) написанное разложение на простейшие
приводят к общему знаменателю и вновь сворачивают в правильную рациональную
дробь ; в) приравнивают коэффициенты при
одинаковых степеняхx в числителях
исходной дроби и получившейся дроби; г) решают полученную систему линейных
уравнений и определяют Bij. Продемонстрируем этот метод на примере . Пример. Вычислить. продемонстрируем алгоритм по пунктам а) пишем разложение на простейшие с
неопределёнными коэффициентами б) приводим разложение на простейшие к
общему знаменателю. и раскрываем получившийся в числителе
полином в) сравнивая коэффициенты при одинаковых
степенях x y исходной функции и
получившегося выражения, получим Решая эту систему, получим A=2 B=3 C=-1 D=2 так что г) интегрируем Комбинированный метод Метод неопределённых коэффициентов
достаточно трудоёмок .Однако заметим что коэффициенты при старших степенях Поэтому реально комбинируют оба этих метода
:коэффициенты при Пример. В том же самом примере находим так что приводя к общему знаменателю получим Случай 3. Подынтегральная функция имеет вид Разложение
этой функции на простейшие имеет вид. т.е. от сомножителя Коэффициенты при старших степенях Пример. Вычислить Так как N и M находим методом неопределённых
коэффициентов Так как это должно быть равно Отсюда Общий случай правильной рациональной дроби
мы рассматривать не будем . В заключение отметим , что есть
рациональная дробь неправильная , т. е. Степень полинома , стоящего в
числителе , выше степени полинома, стоящего в знаменателе , то следует поделить
эти полиномы друг на друга, выделить целую часть и затем интегрировать отдельно
полученную целую часть и оставшуюся правильную рациональную дробь. Пример. Вычислить Решение . Делим полиномы друг на друга 1 Таким образом и поэтому Последний интеграл уже вычислен выше. “Практическая часть к курсовой работе”. §“Реализация метода простых коэффициентов в Maple”. Для
определения конкретных значений сих коэффициентов следует привести равенство к
общему знаменателю и сравнить коэффициенты при одинаковых степенях x в числителе. Т.е. по сути дела решить систему
линейных уравнений. Используется эта конструкция по большей части при
вычислении интегралов, т.к. таким образом интеграл произвольной рациональной
функции сводится, по сути дела, к сумме табличных интегралов. Этакая лекция по
мат. анализу получилась. Сразу
скажу тем, кому вообще лень что-то делать по этому поводу. Maple делает все, что мы сейчас напишем, одной операцией: > сonvert(rfun, parfrac, x); Ивсе. Спросите:
зачем этот велосипед? Цель — не конечный результат, а идея и методы ее
реализации на Maple. Гораздо интереснее
получается посмотреть на целую программу, реально работающий универсальный
алгоритм, делающий конкретно нечто, чем просто читать обрывки help-ов под каждую команду языка на английском, не понимая
в принципе, как это все связать воедино. Ясное дело, профессионалу,
прочувствовавшему Maple, будет неинтересно читать
подробные объяснения по поводу использованных функций языка, однако для
изучающего систему “не совсем новичка”-математика это будет крайне полезно.
Постараюсь в процессе показать читателю свое разумение философии пакета. Как
всегда первый вопрос: с чем работаем? Действительно, для отладки алгоритма
необходимо создать хоть несколько рациональных дробей. Руками писать неудобно,
поэтому даже этот этап “сгрузим” на машину. > restart: > readlib(randomize): (а) > randomize(): (б) > d1:= rand(1..3): > d2:= rand(2..7): (в) > px:= randpoly(x,
degree=21, coeffs=rand(-7..7), terms = 9): (г) > for i from 1 to 3 do > q[i]:= randpoly(x,
degree=1, coeffs=rand(-7..7))^d1(): > q[i+3]:= (x^2 + x +
d2())^d1(): > od: (д) > rfun:=
px/product(q[k], k=1..6); Разберемся,
что тут мы с вами наворотили. Итак, сначала подробно остановимся на генерации
случайных целых чисел в системе Maple. (а) —
здесь мы заставляем генератор случайных чисел привязаться к системному времени.
Если этого не сделать, то генерируемая последовательность будет каждый раз
одинаковой. Вызов просто функции rand() без
аргументов возвратит двенадцатизначное случайное натуральное число. В
большинстве случаев это ну совсем неудобно. Можно это дело исправить, передавая
функции один аргумент: rand(n) , что приведет к генерации числа из полуинтервала
[0, n) . Зачастую и этого недостаточно для решения
поставленной задачи. Можно еще более сузить “область значений” — (б). Только в
этом случае в d1 вернется отнюдь не число, а
ссылка на процедуру, вызов которой приведет к генерации случайного числа из
заданного отрезка. Произвольный полином максимальной степени 21 степени с
коэффициентами из отрезка [-7,7] и девятью членами получим в (в) . Дальше
интереснее — нужно изготовить знаменатель. “Сделаем” его в виде произведения
трех многочленов первой, и трех — второй степени. Причем по определению
многочлены второй степени не должны иметь действительных корней. Реализующая
эту задачу конструкция (г) очевидна и в пояснениях не нуждается. И наконец,
собрав числитель и знаменатель в одно целое, в (д) получим нашу рациональную
дробь. Выражение product(q[k], k=1..6); является формальным переводом на язык Maple записи: Знаменатель
полученной функции таким образом уже будет разложен на множители. Для того
чтобы задача приняла более правдоподобный характер, вместо (д) можно
реализовать следующее: > rfun:=
px/expand(product(q[k], k=1..6), x); Expand раскроет скобки и приведет подобные слагаемые
относительно переменной x в знаменателе.
В итоге получится настоящая рациональная дробь. То, что коэффициенты целые, —
общности задачи не ограничивает — с таким же успехом мы могли сгенерировать их
и иррациональными. Если
запустить все написанное, исключив строку (а) (генератор случайных чисел будет
стандартно инициализирован), получится в точности: Заметили?
В знаменателе появилась “не заказанная” шестая степень. И вместо шести
множителей получилось только пять. Ну и что? Просто два “произвольных”
многочлена полностью совпали (и по степеням тоже). На что только ни способен
генератор случайных чисел в Maple! Результат
раскрытия можно посмотреть на рисунке — там он выглядит куда меньше. Второй
этап работы заключается в определении характера правильности дроби и выделении
целой части (если нужно), т.е. представлению ее в виде: где
Z(x) — целая
часть, а R(x) не делится на Q(x) . Сделаем это
следующим образом: >
fracpart:= rem(numer(rfun), denom(rfun), x, 'zpart'); Заведем
переменную fracpartи zpart
соответственно для дробной и для целой части рациональной дроби.
Процедура-функция rem возвращает остаток от деления
многочленов как основной результат. Третий (необязательный) параметр — имя
переменной, “в которую будет вычислена” целая часть. Совершенно аналогично
действует функция quo , где основным результатом
является целая часть от деления. Здесь функции numer и denom
соответственно дают доступ к числителю и знаменателю дроби. Сейчас
начинается интересное, а именно: попытка записать, собственно, само разложение
с неопределенными коэффициентами. Для начала нужно проанализировать структуру
знаменателя. Разложим его на множители: >
denomx:= factor(denom(rfun)); Разделим
текущую подзадачу на два этапа: “изготовление” списка знаменателей будущих
простейших дробей и запись самого разложения. Для реализации первого этапа нам понадобится
написать процедуру-функцию, которая бы занималась преобразованием выражения
вида An в
упорядоченный список вида [A, A 2 , A 3 , ..., An ]. (а) > transpol:= proc (p:
polynom) local j; (б) > if degree(p, x) <=
1 then > p; > else (в) > if not type(op(2, p),
numeric) then > p; > else (г) > seq(op(1, p)^p, j=1..
op(2, p)); > fi; > fi; > end: В
(а) объявим имя функции, тип и количество передаваемых параметров, а также
локальные переменные в поле local .
Результатом работы функции будет результат последней выполненной операции.
Теперь опишем сам алгоритм. Если была передана константа либо многочлен первой
степени, то вернется он же — (б) . Дальше получим и проанализируем тип объекта op(2, p) . Здесь я
обращаюсь к многочлену p как к списку. Maple позволяет работать почти с любым из своих объектов
как со списком. После проверки (б) у нас останется лишь три варианта для p : (x 2 +bx+c), (x 2 +bx+c) n , (ax+b) n . Их op(2, p) будет соответственно равен x 2 , n, n . В первом случае (наш “op” — не число) придется возвратить параметр в
первозданном виде — это просто квадратный неприводимый трехчлен, а в остальных
— осуществляем разложение (г) — формируем нужную последовательность. Далее
приготовим список знаменателей будущих простейших дробей, используя только что
написанное: > ds:= [seq(transpol(op(k,
denomx)), k=1.. nops(denomx))]; В
нашем конкретном случае результат с точностью до расположения элементов списка
будет выглядеть следующим образом: ds:= [2, 2x+3, 5x-4, 4x-1,
(4x-1) 2 , (4x-1) 3 , x 2 +x+2, x 2 +x+4, (x 2 +x+4) 2 , ...,(x 2 +x+4) 6 ] Записать
разложение с неопределенными коэффициентами, имея такую прелесть, ничего не
стоит: > rxn:= 0: > lastvar:= 1: > for i from 1 to nops(ds)
do (а) > if degree(op(1, op(i,
ds)), x) = 1 then (б) > rxn:= rxn +
(A[lastvar])/op(i, ds); > else (в) > rxn:= rxn +
(A[lastvar]*x+A[lastvar + 1])/op(i, ds); > lastvar:= lastvar + 1; > fi; > lastvar:= lastvar + 1; >
od: Теперь
все сначала и по порядку. Заведем переменную rxn , в которую после запишем разложение. Счетчик lastvar уже использованных индексов коэффициентов установим в
значение 1 (следующий, не использованный индекс). Далее, пробегая по списку ds знаменателей будущих простейших дробей, анализируем
их степень. Собственно сама реализация такого анализа (а) может показаться
довольно странной. Со встроенной функцией degree все понятно — она возвратит степень многочлена
относительно переменной, переданной в качестве второго параметра. Что же значит
запись op(1, op(i, ds))? Так как
вариантов здесь только два, то их и рассмотрим. Если op(i, ds) — выражение вида (x 2 +bx+c) n либо (x+d) n , то op(1, op(i, ds)) вернет то, что находится в скобках. В другом случае
— x 2 +bx+c либо x+d (скобок нет) — такая композиция возвратит высший член
многочлена (он записан в лексикографическом виде). Таким образом реализуется
определение степени знаменателя без учета кратности . А дальше, в зависимости
от этого формируется числитель степени на единицу меньшей. За что люблю Maple, так это за (б) и (в) . Ну где вы видели, чтоб вот
так “на ходу” можно было “собрать” переменную? А здесь возможно и такое.
Естественно, использовав очередной индекс, необходимо увеличить значение
счетчика. Итак,
нечто весьма похожее на разложение, приведенное в теореме, мы получили. Теперь
дело за малым — нужно вычислить эти самые Ak -ые. Сделаем
это так: приведем полученное разложение к общему знаменателю, разберемся с
подобными и соберем коэффициенты перед xi , где i = 0 ... 21 (в нашем случае) в числителе: >
f:= collect(numer(rxn), x): > for i from 0 to degree(f,
x) do > cundef[i]:= coeff(f, x,
i): >
od: Функция
numer , вернув числитель, “по дороге” приведет rxn к общему знаменателю, collect как раз и повыносит за скобки xi . В
переменные (не массив!) cundef
i выделим с помощью функции coeff (третий параметр — степень переменной, остальные два
очевидны) эти самые коэффициенты. Их количество будет равно степени f плюс один (нулевая). Зачем это надо? А что у нас во fracpart? Именно — то же самое, но коэффициенты определенные.
Что делаем? Составляем систему линейных уравнений и решаем относительно наших Ak -ых.
Единственность решения такой системы доказана до нас, посему спокойно пишем
дальше: > b:= collect(fracpart, x): (а) > for i from 0 to
degree(f, x) do > cdef[i]:= coeff(b, x, i): >
od: Снова
собрали в cdefi коэффициенты при xi , но уже из fracpart (определенные). Внимание на (а) — их должно быть
столько же, сколько и в первом наборе, иначе система не получится. Сформируем
набор переменных ( Ak- ые), относительно которых будем решать нашу систему
и ее саму: > vars:= {seq(A[k],
k=1..lastvar-1)}: > eqns:=
{seq(cundef[i]=cdef[i], i=0.. degree(f, x))}: > assign(solve(eqns,
vars)); Последняя
строка заставит Maple пошевелить мозгами, решить
нашу систему относительно наших переменных. Функция solve требует два параметра: первый — это набор уравнений,
второй — набор переменных. Результат работы будет представлен в виде опять же
набора равенств. На этом этапе присвоения переменным, относительно которых
решалась система, вычисленных значений не происходит. Чтобы это все-таки
сделать, воспользуемся функцией assign в
качестве параметра, которой передается набор равенств. Таким образом вычислены
наши неопределенные Ak -ые. Так как rxn через них выражается, то на результат можно
посмотреть так (см. рисунок): >
zpart + rxn; Это
и есть разложение нашей rfun на сумму
простейших дробей. >
simplify(zpart + rxn — rfun); осуществит
проверку тождественности (функция simplify
как можно дальше упростит выражение), возвратив 0. Другого и не должно быть, в
противном случае алгоритм сработал некорректно, чего я от него никак не жду. Приведенный
пример лишний раз доказывает, что система Maple никак не является просто символьным калькулятором. В
отличие от MathCad, где возможности
программирования представлены не на высшем уровне, она позволяет реализовывать
самые буйные фантазии по части построения сложнейших алгоритмов. unit Unit1; interface uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls,
Forms,
Dialogs, Spin, StdCtrls, Grids, MatUtilits; type signs =
-1..1; polinom
= array of real;
fpolinoms = array of polinom; TForm1
= class(TForm)
StringGrid1: TStringGrid;
Edit1: TEdit;
StringGrid2: TStringGrid; Edit2: TEdit;
SpinEdit1: TSpinEdit;
SpinEdit2: TSpinEdit;
Button1: TButton;
Memo1: TMemo;
Edit3: TEdit;
Label1: TLabel;
Label2: TLabel;
Edit4: TEdit;
procedure Button1Click(Sender: TObject);
procedure SpinEdit1Change(Sender: TObject);
procedure SpinEdit2Change(Sender: TObject);
procedure FormCreate(Sender: TObject); private {
Private declarations } public {
Public declarations }
procedure Polinommul(a:polinom;n:byte;b:polinom;m:byte;var ab:polinom;var
nm:byte);
procedure GetPolinom(r:fpolinoms;step:byte;flag:boolean;numdrob:byte;var
res:polinom);
procedure Calculate(mass1:polinom;n:integer;var formula:string); end; const n10 =10; var Form1:
TForm1;
n1,n2,s1,s2:shortint; roots1,roots2,znamen,matr:fpolinoms;
pol1,pol2,chislit:polinom;
matr1,koef:matdouble;
mass1:array of real;
elem:array[0..n10] of string[10];
equation,eq1,eq2,eq3:string; implementation {$R *.dfm} Процедура
перемножения объектов типа polinom, т. е.
массивов с коэффициентами многочленов и получения результата их перемножения: procedure
TForm1.Polinommul(a:polinom;n:byte;b:polinom;m:byte;var ab:polinom;var
nm:byte); var temp:real; i,j,t:shortint; p1:polinom; begin setlength(p1,m+n+1); setlength(ab,m+n+1);
temp:=0; for
i:=0 to m+n dop1[i]:=0; for
i:=0 to n do for
j:=0 to m do
begin
temp:=a[i]*b[j];
p1[i+j]:=p1[i+j]+temp; end;
nm:=n+m; ab:=p1; { t:=0; for
i:=0 to m+n do if
p1[i]=0 then
begin t:=i+1;
continue; end else
break; setlength(ab,m+n-t); for i:=
0 to m+n-t+1 do
ab[i]:=p1[i+t]; nm:=m+n-t+1;
} end; Процедура,
которая из массива многочленов делает многочлен – или результат их перемножения
– или произведение, но без i-го члена, в
зависимости от flag. procedure
TForm1.GetPolinom(r:fpolinoms;step:byte;flag:boolean;numdrob:byte;var
res:polinom); var
buffer,buffer1,temp:polinom;
i,j,p,p1:byte;
flag1:boolean; begin if not(flag) then begin
setlength(buffer,2); setlength(buffer1,2);
setlength(temp,2);
buffer[0]:=r[0,0];
buffer[1]:=r[0,1]; p:=1; p1:=1; for
i:=1 to step do
begin
setlength(temp,p1+1);
for j:=0 to 1 do
buffer1[j]:=r[i,j];
Form1.Polinommul(buffer,p,buffer1,1,temp,p1);
setlength(buffer,p1);
buffer:=temp;
p:=p1; end; end else begin
setlength(buffer,2);
setlength(buffer1,2);
setlength(temp,2);
buffer[0]:=0;
buffer[1]:=1.0; p:=0; p1:=0; for
i:=0 to step do
begin
if numdrob = i then
begin
buffer1[0]:=0;
buffer1[1]:=1.0;
end;
if numdrob<>i then inc(p);
if numdrob<>i then for j:=0 to 1 dobuffer1[j]:=r[i,j];
if numdrob=i then begin
Form1.Polinommul(buffer,p,buffer1,1,temp,p1);
continue;
end;
Form1.Polinommul(buffer,p,buffer1,1,temp,p1);
if numdrob<>i then setlength(buffer,p1);
buffer:=temp;
end; end; setlength(res,p1); res:=buffer; end; Основной
текст программы, вбирающий в себя процедуры и реализовающий сам процесс
разложения на простые множители. Его я повесил на кнопку: procedureTForm1.Button1Click(Sender: TObject); var
i,j,k:byte;
temp:polinom;
st1,st2,st3,stt:string; begin Form1.Edit1.Text:=''; Form1.Edit2.Text:=''; Form1.Edit3.Text:=''; Form1.Edit4.Text:=''; n1:=strtoint(Form1.SpinEdit1.Text); n2:=strtoint(Form1.SpinEdit2.Text)-1; setlength(chislit,n1+1); setlength(roots2,n2+1,2); setlength(znamen,n2,n2); for i:=0 to n1 do begin
chislit[i]:=strtofloat(Form1.StringGrid1.Cells[i,0]); end; for i:=0 to n2 do begin
roots2[i,0]:=1.0;
roots2[i,1]:=-strtofloat(Form1.StringGrid2.Cells[i,0]); end; form1.GetPolinom(roots2,n2,false,0,pol2); setlength(temp,n2+1); for i:=0 to n2 do begin for
k:=0 to n2 do temp[k]:=0;
form1.GetPolinom(roots2,n2,true,i,temp); for
j:=0 to n2 do
Form1.Edit3.Text:= Form1.Edit3.Text+getfstring(temp[j+1],1)+' '; for
k:=0 to n2 do temp[k]:=0; end; form1.Calculate(chislit,n1+1,st1); form1.Calculate(pol2,n2+2,st2); Form1.Edit1.Text:=st1; Form1.Edit2.Text:=st2; {for i:=0 to n1 do
Form1.Edit1.Text:=Form1.Edit1.Text+getfstring(chislit[i],1)+' '; for i:=0 to n2+1 do
Form1.Edit2.Text:=Form1.Edit2.Text+getfstring(pol2[i],1)+' ';} Setlength(matr,n2+2,n2+1); for i:=0
to n2 do begin
form1.GetPolinom(roots2,n2,true,i,temp); for
j:=1 to n2+1 do matr[i,j-1]:=temp[j]; end; i:=0; for j:=0
to n2 do
matr[n2+1,j]:=0; for
j:=n2-n1 to n2 do begin
matr[n2+1,j]:=chislit[i];
inc(i); end; setlength(matr1,n2+1,n2+2); setlength(koef,n2+1,1); for i:=0
to n2 do for
j:=0 to n2+1 do
matr1[i,j]:=matr[j,i];
korni(matr1,n2+1,n2+2,koef); for i:=0
to n2 do
form1.Edit4.Text:=form1.Edit4.Text+getfstring(koef[i,0],3)+' '; end; procedure TForm1.SpinEdit1Change(Sender:
TObject); begin Form1.StringGrid1.ColCount:=strtoint(Form1.SpinEdit1.Text)+1; end; procedure TForm1.SpinEdit2Change(Sender:
TObject); begin Form1.StringGrid2.ColCount:=strtoint(Form1.SpinEdit2.Text); end; procedure TForm1.FormCreate(Sender: TObject); var i:shortint; begin Form1.StringGrid1.ColCount:=strtoint(Form1.SpinEdit1.Text)+1; Form1.StringGrid2.ColCount:=strtoint(Form1.SpinEdit2.Text); end; Чтобы
вид был более нагляден и информативен, я использовал процедуру преобразования
массива коэффициентов: procedure
TForm1.Calculate(mass1:polinom;n:integer;var formula:string); var i,j,k1:byte; sign:array of signs ; first,flag:boolean; odin:array of boolean; s:integer; begin k1:=n-1; for i:=0 to n-1 do begin
elem[i]:='x^'+inttostr(k1);
dec(k1); end; first:=true; setlength(odin,n); setlength(sign,n); setlength(mass1,n); equation:=''; for i:=0
to n-1 do//calculating and
building begin if abs(mass1[i])=1 then odin[i]:=true; //esli ediniza if
mass1[i]>0 then sign[i]:=1
//check sign
else
if mass1[i]=0 then sign[i]:=0
else sign[i]:=-1; if
odin[i] then//esli ediniza
begin if
i
case sign[i] of 1:
if first then
begin
equation:=equation+elem[i];
first:=false;
end
else
equation:=equation+' + '+elem[i]; 0:
continue; -1:
begin
if first then first:=false;
equation:=equation+' - '+elem[i];
end;
end
else
case sign[i] of 1:
if first then
begin
equation:=equation+'1';
first:=false;
end
else
equation:=equation+' + 1'; 0:
continue; -1:
begin
if first then first:=false;
equation:=equation+' - 1';
end;
end;
continue; end; if
i = n-1 then
case sign[i] of 1:
if first then
begin
equation:=equation+getfstring(abs(mass1[i]),3);
first:=false;
end
else
equation:=equation+' + '+getfstring(abs(mass1[i]),3);
0:continue; -1:
begin
if first then first:=false;
equation:=equation+' - '+getfstring(abs(mass1[i]),3);
end; end else
case sign[i] of 1:
if first then
begin
equation:=equation+getfstring(abs(mass1[i]),3)+'*'+elem[i];
first:=false;
end
else
equation:=equation+' + '+getfstring(abs(mass1[i]),3)+'*'+elem[i]; 0:
continue; -1:
begin equation:=equation+' -
'+getfstring(abs(mass1[i]),3)+'*'+elem[i];
if first then first:=false;
end; end; end; s:=0; { for i:=0 to n-1 do
s:=s+abs(mass1[i]); if s=0
then equation:='0';} formula:=equation; end; end. Пример: В
моей курсовой работе я рассмотрел подробно метод простых коэффициентов и
реализовал программу на Delphi, которая
вычисляет значения коэффициентов для случая простых действительных корней
знаменателя. В Mapleэта процедура тоже есть и вычисляет коэффициенты для
любой дробно – рациональной функции. Нехватка времени не позволила мне довести
мою программу до полной функциональности: вычисление коэффициентов для любого
знаменателя, т. е. знаменателя с любыми корнями. В дальнейшем, может быть, я
это осуществлю. Однако, даже в таком варианте она полезна для практического
использования – быстрого вычисления коэффициентов. Список литературы. 1.Бахвалов Н.С., Лапин А.В.,
Кобельков Г. М. Численные методы. – М.: Физматлит, 2001. 2.Волков Е.А. Численные
методы. – Петербург, изд – во «Лань», 2004. 3.Демидович Б.П., Марон И.А.
Основы вычислительной математики. - М.: Наука, 1970. 4.Вержбицкий В.М. Численные
методы. Линейная алгебра и нелинейные уравнения. - М.: Высшая школа, 2000. 5.Бахвалов Н.С., Лапин А.В.
Численные методы в задачах и упражнениях. – М.: Высшая школа, 2000. 6.Фаддеев Д.К., Фаддеева
В.Н. Вычислительные методы линейной алгебры. – Петербург, изд –во «Лань», 2002. 7.Самарский А.А., Гулин А.В. Численные методы
математической физики. – М.: Научный мир, 2003. 8.Деммель Дж. Вычислительная линейная алгебра. – М.:
«Мир», 2001. 9.Косарев
В.И. 12 лекций по вычислительной математике. – М.: изд –во МФТИ, 2000. 10.Лобанов
А.И., Мещеряков М.В., Чудов Л.А. Задачи для самостоятельного исследования в
курсе вычислительной математики. – М.: изд –во МФТИ, 2001  ,
, различны и m
различны и m
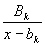 называются простейшими , а само приведённое разложение называется
“разложением рациональной дроби на простейшие”.
называются простейшими , а само приведённое разложение называется
“разложением рациональной дроби на простейшие”. . Рассмотрим , например , вычисления
. Рассмотрим , например , вычисления 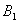 . Для этого
. Для этого 


 означает , что в написанном слева выражении надо положить
означает , что в написанном слева выражении надо положить  )
) . Этот метод получил название “метода вычёркивания “. Он
формулируется так : чтобы вычислить коэффициент
. Этот метод получил название “метода вычёркивания “. Он
формулируется так : чтобы вычислить коэффициент  нужно
нужно
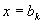 .
.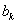 найдены, то дальнейшее очень просто
найдены, то дальнейшее очень просто  и получившиеся интегралы 1 типа легко вычисляются
и получившиеся интегралы 1 типа легко вычисляются 
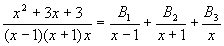
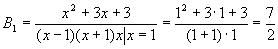


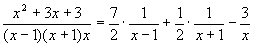

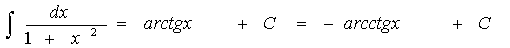
 т.е. сомножитель вида
т.е. сомножитель вида 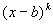 даёт группу слагаемых вида
даёт группу слагаемых вида 

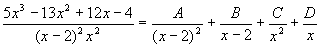

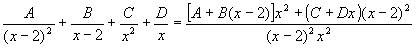





 , т.е. при
, т.е. при  можно определять методом вычёркивания.
можно определять методом вычёркивания. определяют методом вычёркивания , а оставшиеся – методом
неопределённых коэффициентов.
определяют методом вычёркивания , а оставшиеся – методом
неопределённых коэффициентов.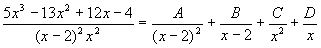
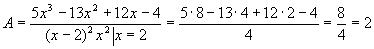
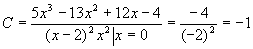
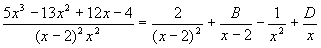 ,
,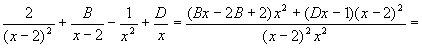
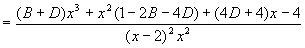 .
.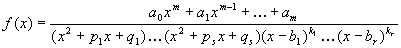
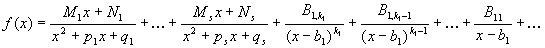

 идёт слагаемое вида
идёт слагаемое вида 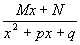 . Оно при интегрировании даст интеграл третьего типа.
. Оно при интегрировании даст интеграл третьего типа.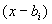 , т.е. при
, т.е. при 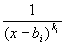 находятся методом вычёркивания , остальные – методом неопределённых
коэффициентов.
находятся методом вычёркивания , остальные – методом неопределённых
коэффициентов.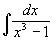
 , то
, то 
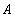 находим методом вычёркивания
находим методом вычёркивания 

 то имеем
то имеем  при
при  и при
и при 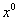 )
) 
 (В последнем интеграле N=2 , M=1, p=1, q=1).
(В последнем интеграле N=2 , M=1, p=1, q=1). 




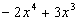







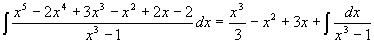
Часть 2.
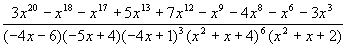

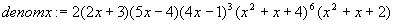

§ “Реализация метода простых коэффициентов на Delphi”.
Листинг:


Заключение.