Квазистатический метод анализа случайных процессов в нелинейных системах

Примечание	от автора: с книги автор - Тихонов
	Загрузить архив:
	Файл: ref-25524.zip (938kb [zip], Скачиваний: 125) скачать

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ГРАЖДАНСКОЙ АВИАЦИИ

                                                      Кафедра ОРТЗИ

РЕФЕРАТна тему

«КВАЗИСТАТИЧЕСКИЙ МЕТОД АНАЛИЗА СЛУЧАЙЙНЫХ ПРОЦЕССОВВ НЕЛИНЕЙНЫХ   СИСТЕМАХ»

по дисциплине

«Теория помехоустойчивости».

Выполнил:

Студент группы БИ 4-2

Зыков Антон В.

Москва - 2018

МЕТОДЫ АНАЛИЗА СЛУЧАЙЙНЫХ ПРОЦЕССОВВ НЕЛИНЕЙНЫХ   СИСТЕМАХ

                       1. ФОРМУЛИРОВКА    ЗАДАЧИ.    МЕТОДЫ АНАЛИЗА

В соответствии с классификацией преобразований cл. пр., рассмотрим детерминированные нелинейные инерционные преобразования. При таких преобразованиях ин­тересующий нас процесс на выходе нелинейной системы η(t) связан с входным процессом ξ(t) нелинейным дифференциальным уравнением. Вид этого уравнения определяется конкретной си­стемой или устройством.

В качестве примеров типовых нелинейных радиотехнических систем можно указать следующие: все автоколебательные системы (автогенераторы гармонических и импульсных колебаний), нели­нейные усилители и детекторы различных видов, модуляторы, разнообразные следящие системы (фазовая и частотная автопод­стройки, дальномеры, автомагическая регулировка усиления), триггеры и др. При этом следует различать два вида или класса моделей нелинейных систем: системы, представляющие собой разные комбинации нелинейных безынерционных устройств

Рис. 1. Пример нелинейной системы

и линейных звеньев и системы, описыва­емые нелинейными дифференциальными уравнениями.

Анализ моделей нелинейных систем первого вида по существу сводится к раздельному пересчету вероятностных характеристик сл. пр. через нелинейные безынерционные устройства и линейные системы; правила таких пересчетов были рассмотрены ранее.

Пусть, например, требуется вычислить корреляционную фун­кцию на выходе нелинейной системы (рис. 5.1), состоящей из двух нелинейных безынерционных устройств, между которыми включена линейная система с импульсной характеристикой h(t), при нулевых начальных условиях:

     (1.1)

Отсюда видно, что для вычисления требуемой корреляционной функции необходимо знать двумерную п. в. процесса ξ(t) на выходе линейной системы. Если принять, что входной процесс ξ(t) гауссовский, то процесс η(t) на выходе первого нелинейного элемента будет негауссовским и задача определения двумерной п.в. p_ξ(ξ₁, ξ₂, t_1, t₂) может быть решена лишь приближенно. Приведенные рассуждения можно обобщить на нелиней­ные системы, описываемые функциональными рядами Вольтерра .

Встречаются трудности при анализе ел. пр. в нелинейных системах второго вида, описываемых нелинейными дифференци­альными уравнениями. Будем говорить, что система имеет порядок k, если она описывается дифференциальным уравнением k-го порядка. Применительно к нелинейной системе первого порядка нелинейное дифференциальное уравнение может, напри­мер, иметь вид

(1.2)

Вид функций f(•) и g(•) определяется параметрами рассмат­риваемой системы.Для  детерминированнойсистемы   (преоб­разования) эти функции считаются детерминированными и извест-Если функции f и gнелинейны относительно η, то (2) eсть нелинейное дифференциальное уравнение первого порядка.

В том случае, когда входное воздействие ξ(t) содержит белый шум п((), уравнение принято называть стохастическим диф­ференциальным уравнением. Если же ξ(t) содержит только кор­релированное воздействие (cл. пр. с конечным, не нулевым интервалом корреляции), то соответствующее дифференциальное уравнение будем называть флюктуационным дифференциальным уравнением, хотя в литературе встречаются и другие названия (уравнение Ланжевена, кинетическое уравнение}.

Формулировка задачи анализа остается прежней: предполагая известными параметры модели системы, т. е. конкретный вид уравнения (2) и необходимые вероятностные характеристики входного процесса (воздействия) ξ(t), требуется найти нужные вероятностные характеристики выходного процесса η(t). Те характеристики выходного процесса η(t), которые нужно нахо­дить, определяются физическим содержанием конкретной задачи. Обычно интересуются моментами (чаще всего м. о. и корреляци­онной функцией) выходного процесса η(t) или же п. в. (чаще одномерной и реже двумерной).

Известно, что характер решения нелинейного дифференци­ального уравнения зависит от его вида, формы внешнего воздействия и начальных условий, причем в общем случае невозможно записать решение в квадратурах. В этом состоит существенное отличие нелинейных инерционных преобразований ел. пр. от линейных, для которых выходной процесс выражается через входной с помощью интеграла свертки.

По этой же причине нелинейные инерционные преобразования принципиально отличаются от безынерционных преобразований и сводящихся к ним. При безынерционных (функциональных) преобразованиях ел. пр. известны сравнительно простые методы «пересчета» вероятностных характеристик (9). Для нелинейных инерционных преобразований не существует единого метода решения.

Метод решения нелинейных флюктуационных дифференциальных уравнений, в частности уравнения (2), определяется двумя фактора­ми: 1) интенсивностью случайного воздействия !;(/) и 2) отношением интервала корреляции t_к. воздействия к характерной постоянной времени системы t_с. При этом, говоря об интенсивности случайного воздействия, здесь имеем в виду не фактическую величину самого сл. пр. ξ(t) (например, величину его дисперсии), а вызываемый им в системе эффект (случайный разброс). Отметим, что если система сложная и характеризуется несколькими постоянными времени, то в качестве времени тс следует брать минимальное из них. Аналогично, ели внешнее случайное воздействие ξ(t) характеризуется нескольки­ми временами, то под t_к следует понимать максимальное из них зависимости от указанных двух факторов можно указать следующие частные случаи и соответствующие методы их рассмотрения.

1. Случайное воздействие малой интенсивности. В данном случае независимо от соотношения t_к и t_с применим метод линеаризации. Он заключается в том, что сначала находится решение исходного нелинейного дифференциального уравнения в отсутствие малого случайного воздействия, а затем уравнение линеаризуется относительно малых случайных отклонений от невозмущенных значений и делается пренебрежение нелинейными членами, содержащими эти случайные отклонения. В результате для случайных отклонений получается линейное дифференциаль­ное уравнение. Методы преобразования cл. пр. линейными системами были рассмотрены ранее.

Метод линеаризации позволяет сравнительно просто вычис­лить м. о. и корреляционную функцию процесса η(t) в стаци­онарном и нестационарном состояниях. Однако при негауесовском возмущении ξ(t) весьма трудно (например, методом вычисления моментов) найти даже одномерную п. в. для η(t).

2. Случайное воздействие большой интенсивности. Здесь нет единого и универсального метода решения; выбор метода зависит от соотношения t_к и t_с.

a. Если t_с>>t_к и входное воздействие ξ(t) представляет собой гауссовский cл. пр, то применим хорошо разработанный аппарат марковских процессов. В частности, для анализа поведения динамических систем можно использовать известное уравнение ФПК, а задачи, связанные с достижением границ (срывом слежения и автозахватом), решать с помощью уравнения Пон-трягина. Данный случай характерен для многих следящих ра­диотехнических устройств. Метод марковских процессов даже в существенно нелинейных задачах в принципе позволяет находить непосредственно п. в. выходного процесса η(t). Сложность фак­тического получения решения для конкретной задачи существенно зависит от порядка дифференциального уравнения, описывающего поведение рассматриваемой системы, и вида начальных и гранич­ных условий.

К настоящему времени аналитическими и численными ме­тодами получено много важных и оригинальных результатов в основном для одномерных и двумерных нелинейных систем. Применительно к динамическим системам, описываемым диф­ференциальными уравнениями третьего и более высоких порядков, часто возникают трудности в получении точных и компактных аналитических и численных результатов. В подобных случаях, когда возникают затруднения, иногда можно продуктивно вос­пользоваться явлением нормализации ел. пр. на выходе инер­ционной системы.При этом заранее принимается,что п. в. выходного -процессаявляетсянормальной,  изатемтем или иным способом вычисляются ее определяющие параметры. В ча­стности, если дисперсия выходного процесса мала, то ее можно определять из линеаризованного уравнения, а м. о. из нелинейногоуравнения. Кроме такого метода применяют также квазилинейный метод (часто называемый методом статистической линеаризации). При его применении предполагается заранее известной п. в. выходного процесса, и поэтому он часто фактически базируется на том же явлении нормализации.

b. При t_с«t_к можно ограничиться решением задачи в ква­зистатическом приближении. Оно характеризуется тем, что в пер­вом приближении делается пренебрежение временной производ­ной, например в уравнении (2). После этого задача сводится к нелинейному безынерционному преобразованию

                      (1.3)

Решив это уравнение относительно η(t), получим η(t) = F(t, ξ,(t)).

При квазистатическом приближении внешнее случайное воз­действие считается настолько медленно изменяющимся, что система с определенной деформацией безынерционно отслеживает его. В некоторых задачах при сведении инерционного нелинейного преобразования к безынерционному целесообразно воспользовать­ся методом осреднения Н. Н. Боголюбова.

в. Случай промежуточных времен корреляции (tс~t.к) является наиболее сложным при анализе. Ряд нелинейных систем при таком условии можно анализировать, используя функциональное представление Вольтерра нелинейных дифференциальных ура­внений2.

Отметим, что области применения перечисленных методов анализа принципиально не ограничиваются порядком нелинейного дифференциального уравнения. Однако с повышением порядка уравнения существенно возрастает трудоемкость вычислений.

В дальнейшем проиллюстрируем методику применения разных методов на конкретных радиотехнических примерах, рассмотрение которых представляет самостоятельный интерес.

                                       2. КВАЗИСТАТИЧЕСКИЙ МЕТОД

Общие условия применения квазистатического метода и его сущность были кратко указаны выше. Получим этим методом конкретные результаты применительно к детектированию

Рис. 2. Упрощенная схема типового радиоприемника

Рис. 3. Схема амплитудного де­тектора

ставить в виде (7.42): случайных узкополосных процессов. Основными элементами типового радиоприемника являются УПЧ и детектор (рис.2). Обычно УПЧ представляет собой линейный уз­кополосный четырехполюсник. При воздействии на него широкопо­лосного гауссовского шума п({) (например, собственных шумов предыдущих каскадов) и полезного гармонического сигнала 5(0 вы­ходное напряжение можно пред-

(2.1)

Для простоты предполагается, что частота полезного сигнала совпадает с центральной частотой полосы пропускания УПЧ.

Случайное напряжение ξ(t) воздействует на детектор. Найдем характеристики случайного напряжения η(t) на выходе детектора. Проиллюстрируем методику применения квазистатистического метода на примере амплитудного детектора огибающей, схема которого изображена на рис.3.

Пусть нелинейный элемент Д (диод) имеет вольт-амперную характеристику i=g(v), v = ξ — η. Считая равным нулю внутреннее сопротивление генератора входного напряжения ξ(t) из очевидных соотношений

получим дифференциальное уравнение

                                                                   (2.2)

Поскольку назначение любого детектора в радиоприемнике состоит в возможно лучшем выделении модулирующего напряже­ния, то он, во-первых, должен сглаживать радиочастотные колебания и, во-вторых, напряжение на цепи КС должно успевать «следить» за изменениями модулирующего напряжения (приме­нительно к амплитудному детектору следить за огибающей). Выполнение этих двух условий достигается тем, что параметры детектора должны удовлетворять двум неравенствам:

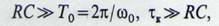       (2.3)

-интервал корреляции огибающей В(t).

Петектор для которого выполняются эти два неравенства, принято называть детектором огибающей. Другие случаи ис­пользования детектора, когда эти условия не выполняются, здесь не рассматриваются .

Выполнение условий (3) существенно упрощает задачу ис­следования процесса детектирования случайных сигналов, так сак при этом выходное напряжение η(t) почти безынерционно (квазистатически) зависит от огибающей В(t).

Проинтегрируем это уравнение за период Т₀:

Подставив (1) в (2)' имеем

                            (2.4)

При выполнении первого условия (3) функция η(t) мало изменя­ется за период Т₀. Поэтому разность η(t+T₀) - η(t) почти не отличается от η(t)Т₀. Медленно изменяющиеся величины под знаком интеграла можно принять приближенно постоянными, т. е. можно положить

и учитывать изменение только cos(wt' + Ψ). Поэтому (4) можно записать как

и это уравнение затруднительно решить в общем виде. Хотя

г и переходный процесс, рассмотрим в дальнейшем

щионарное состояние. Для стационарного состояния при

выполнении второго неравенства (3) можно ограничиться квазистатистическим ограничением

Т. е. в левой части уравнения (5)можно пренебречь производной. После этого получим уравнение

(2.6) дающее безынерционную зависимость выходного напряжения η(t) от огибающей В(t). Здесь при интегрировании по х величины В и г) принимаются постоянными.

Таким образом, при исследовании воздействия узкополосного сл. пр. на детектор огибающей в стационарном состоянии можно ограничиться квазистатическим приближением, т. е. вместо точ­ного дифференциального уравнения (2) можно ограничиться анализом приближенного функционального соотношения (6).

Для линейного детектора огибающей, имеющего характеристику

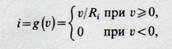
(2.7)

где R₁— внутреннее сопротивление диода в открытом состоянии, из (о) получим

               (2.8)

Безразмерную величину А; можно назвать коэффициентом воспроизведения оги­бающей.

Характерным свойством линейного детектора огибающей, в отличие от других типов амплитудных детекторов, является то, что коэффициент воспро­изведения огибающей k не зависит от значения самой огибающей и определяется только отношением сопротивлений R/R₁. После вычисления коэффициента А; веро­ятностные характеристики выходного напряжения η(t) = kВ(t) просто находятся по соответствующим характеристикам огибающей.

При квадратичном детектировании нелинейная характеристика задается вы­ражением

                                                (2.9)

В данном случае формула (6) приводит к следующему результату:

                                                                                  (2.10)

Теперь коэффициент & не имеет прежнего прямого смысла, поскольку он зависит от значения огибающей В(1).

При βRB≤0,1 выполняется неравенство k«1. Полагая аrccosk=π/2из (10) найдем

                          (2.11)

напряжение пропорционально квадрату огибающей. Для больших значений βRВ коэффициент k можно найти путем численного решения трансцен­дентного уравнения (10).

Укажем, что если в схеме рис.2 за УПЧ включен идеальный ограничитель и вместо амплитудного детектора стоит фазовый или частотный детектор и для них выполняются условия, аналогичные (3), обеспечивающие применимость квазистатичес­кого приближения, то напряжение на выходе фазового детектора будет пропорционально случайной фазе Ψ(t) узкополосного cл. пр. (1), а на выходе частотного детектора - пропорционально мгновенной частоте dΨ(t)/dt

                                                                    ЛИТЕРАТУРА.

1 Стратонович Р. Л. Избранные вопросы теории флюктуации в радиотехнике.— М.: Сов. радио, 1961.—558с.

2 Баруча-Рид А. Т. Элементы теории марковских процессов и их приложения: Пер. с англ./Под ред. А. Н. Ширяева.—М.: Наука, 1969.—512с.

3 Гардинер К. В.   Стохастические   методы   в   естественных   науках: с англ./Под ред. Р. Л. Стратоновича.— М.: Мир, 1986.— 526с.

   4Тихонов. Моделирование нелинейных систем на основе теории Вине-ра//ТИИЭР.- 1981.—Т. 69, № 12—С. 261—269.