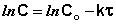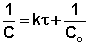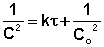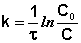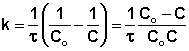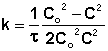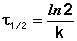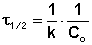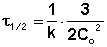Химическая кинетика
| Загрузить архив: | |
| Файл: ref-26917.zip (87kb [zip], Скачиваний: 233) скачать |
Московский Авиационный Институт
Кафедра физической химии
КУРСОВАЯ РАБОТА
на тему: Химическая кинетика
Выполнила: студентка группы 11-102
Мединцева Е. Ф.
Преподаватель: Романенков А. А.
Москва, 2018
Содержание:
1. Введение………………………………………………………………………...3
2. Скорость протекания химической реакции…………………………………..4
3. Зависимость скорости реакции от концентрации реагентов………………...6
4. Порядок химической реакции…………………………………………………7
5. Молекулярность химической реакции………………………………………12
6. Методы определения порядка реакции……………………………………...13
7. Влияние температуры на скорость реакции……………………………..….16
8. Энергия активации……………………………………………………………19
9. Химическое равновесие………………………………………………………22
10. Заключение…………………………………………………………………...25
11. Список литературы………………………………………………………......27
Введение
Данная курсовая работа посвящена одному из разделов общей химии, называемому химической кинетикой или кинетикой химических реакций. Изучает данный раздел механизмы протекания химических реакций, порядок химической реакции, а также закономерности протекания химических реакций во времени.
Начнем со скорости протекания химической реакции. Скорость химической реакции определяется как изменение молярной концентрации одного из реагирующих веществ за единицу времени. Скорость химической реакции - величина всегда положительная, поэтому если она определяется по исходному веществу (концентрация которого убывает в процессе реакции), то полученное значение домножается на -1.
Например, для реакции 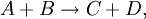 скорость можно выразить так:
скорость можно выразить так:
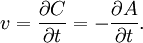
В 1865 году Н.Н. Бекетовым и в 1867 году К.М. Гульдбергом и П. Вааге был сформулирован закон действующих масс, согласно которому скорость химической реакции в каждый момент времени пропорциональна концентрациям реагентов, возведенным в некоторые степени. Кроме концентрации на скорость химической реакции оказывают влияние следующие факторы: природа реагирующих веществ, наличие катализатора, температура и площадь поверхности реагирующих веществ.
Скорость протекания химической реакции
Химическая термодинамика позволяет предсказать принципиальную возможность или невозможность самопроизвольного течения химических реакций, а также рассчитать равновесные концентрации реагирующих веществ. Однако, знание рассмотренных закономерностей еще не достаточно, чтобы предсказать реальную возможность химической реакции, определить скорость реакции и ее механизм, а также управлять процессом.
Скорость химической реакции равна изменению количества вещества в единицу времени в единице реакционного пространства. В зависимости от типа химической реакции (гомогенной или гетерогенной) меняется характер реакционного пространства.
Гомогенная реакция - реакция в одной фазе состояния вещества.
Гетерогенная реакция протекает на границе раздела фаз.
Отношение количества вещества к объёму называется концентрацией (С).
Скорость гомогенной реакции равна изменению концентрации любого из исходных веществ или продуктов реакции во времени. Различают среднюю и мгновенную скорости реакций. (Скорость реакции всегда положительна).
Средняя скорость реакции:
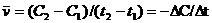 (7.1)
(7.1)
Мгновенная скорость реакции:
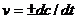 (7.2)
(7.2)
В ходе реакции изменяются концентрации всех исходных веществ и продуктов реакции. Если у всех реагентов одинаковые стехиометрические коэффициенты, то изменения их концентраций (по модулю) во времени также одинаковы. Например, для реакции:
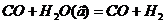
Для реакций с различными стехиометрическими коэффициентами скорости изменения концентрации реагентов будут различными. Для реакции:
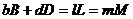
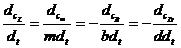
Скорость реакции зависит от природы реагирующих веществ. Некоторые реакции, например взрывы, протекают мгновенно, другие идут годами. На скорость реакции влияют многие факторы: концентрация, температура, катализаторы, внешние воздействия.
Зависимость скорости реакции от концентрации реагентов
Чтобы произошла реакция, необходимо столкновение молекул. При одной температуре число столкновений растёт с увеличением числа реагирующих частиц в единице объёма, т.е. с возрастанием концентрации реагентов.
Скорость необратимой реакции:
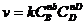 (7.3)
(7.3)
k - константа скорости реакции; 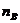
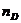 - коэффициенты,
называемые порядками реакции по веществам B и D.
- коэффициенты,
называемые порядками реакции по веществам B и D.
Уравнение (7.3) называется кинетическим уравнением химической реакции.
Константа скорости не зависит от
концентрации реагентов, но зависит от их природы и температуры. Из уравнения
(7.3) следует, что при 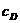
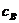
Например, для реакции диссоциации молекулы
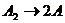
для которой
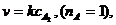
единица измерения константы скорости
реакции, исходя из анализа размерностей, будет равна: 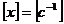
Итак, скорость реакции пропорциональна произведению концентраций реагентов в степенях, называемых порядками реакции по реагентам.
Порядок химической реакции
Сумма порядков реакции по реагентам называется порядком реакции n:
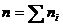 (7.4)
(7.4)
где 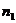 порядок реакции по i реагенту.
порядок реакции по i реагенту.
Если реакция простая, т.е. протекает в одну стадию, то порядок реакции равен сумме стехиометрических коэффициентов:
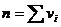
где
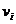 i –
вещества в уравнении реакции (стехиометрический коэффициент).
i –
вещества в уравнении реакции (стехиометрический коэффициент).
Если
bB+dD=lL+mM протекает в одну стадию, то 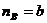 и
и 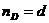 и соответственно в этом случае кинетическое уравнение для указанной
реакции примет вид:
и соответственно в этом случае кинетическое уравнение для указанной
реакции примет вид:
 (7.5)
(7.5)
и называется законом действующих масс для химической кинетики.
Для реакции образования иодида водорода:
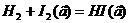
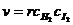 , т.е.
n=1+1=2.
, т.е.
n=1+1=2.
Для многостадийных реакций порядки реакции по реагентам, как правило, не совпадают со стехиометрическими коэффициентами, а общий порядок реакции не равен сумме стехиометрических коэффициентов. В этом случае для расчёта скорости реакции используют кинетическое уравнение (7.3), а не его частный случай- закон действующих масс для кинетики (7.5).
Наиболее часто встречаются реакции первого, второго и иногда третьего порядка. Некоторые реакции имеют дробный порядок (0.5, 1.5). Реакции более высокого порядка чем третий не известны.
Итак, порядок простой (одностадийной) реакции равен сумме стехиометрических коэффициентов, а сложной (многостадийной) реакции ниже этой суммы.
Скорость реакции первого порядка характеризуется кинетическим уравнением
V=kc (7.6)
Первый порядок, например, имеют реакции диссоциации или разложения молекул:
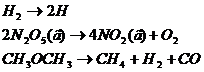
По уравнению (7.2)
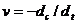
Приравнивая уравнения (7.2) и (7.6) и разделяя переменные, получаем:
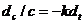
Решение данного уравнения для
начального условия 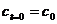 приводит к выражению:
приводит к выражению:
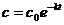 (7.7)
(7.7)
Подставляя уравнение (7.7) в (7.6), найдём
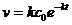 (7.8)
(7.8)
Как видно, концентрация реагентов и скорость реакции первого порядка уменьшается во времени по экспоненциальному закону.
Уравнение (7.7) можно записать в виде
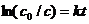 (7.9а)
(7.9а)
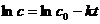 (7.9б)
(7.9б)
Преобразуя уравнение (7.9а), найдём выражение для константы скорости реакции
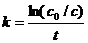 (7.10)
(7.10)
Так как 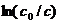 безразмерен, то
константа скорости реакции первого порядка имеет единицу измерения обратного
времени
безразмерен, то
константа скорости реакции первого порядка имеет единицу измерения обратного
времени 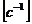
Из графика изменения концентрации реагента во времени (рис 7.1а) легко определяется константа скорости реакции:
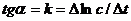
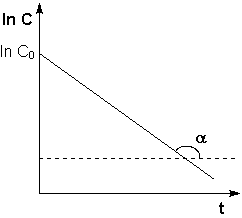
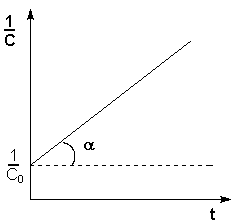
а б
(рис 7.1) изменение концентрации исходных веществ во времени для реакций первого (а) и второго (б) порядков.
В качестве критерия скорости реакции
нередко используется период полураспада 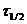
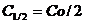
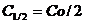 и
и 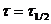 в (7.10), и преобразуя
получаем
в (7.10), и преобразуя
получаем
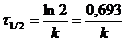 (7.11)
(7.11)
Период полураспада реагента в случае реакции первого порядка не зависит от начальной концентрации, а определяется лишь константой скорости. Реакции по уравнению (7.11) можно рассчитать константу скорости реакции, если известен период полураспада.
Скорость реакции второго порядка для двух B и D подчиняется кинетическому уравнению:
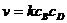 (7.12)
(7.12)
Если
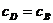 или если реагируют
одинаковые частицы, то
или если реагируют
одинаковые частицы, то
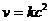 (7.13)
(7.13)
Второй порядок имеют, например реакции разложения йодида водорода и диоксида азота:
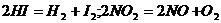
Как показывает анализ, характер изменения концентрации реагента во времени одинаков как для (7.12), так и для (7.13). Используя уравнение (7.2) и разделяя переменные:
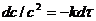
Решение уравнения для начального
условия 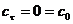 имеет вид:
имеет вид:
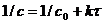 (7.14)
(7.14)
или
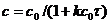 (7.15)
(7.15)
Уравнение (7.15) является уравнением кинетической кривой реакции второго порядка. Как видно концентрация реагента изменяется во времени по сложному закону. Величина обратная концентрации растёт во времени линейно. Из уравнения (7.14) получим выражение для константы скорости реакции
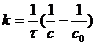 (7.16)
(7.16)
Из анализа единиц измерения уравнения
(7.16) с 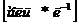 и
и 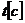 k
k 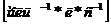
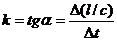
Период полупревращения в данном случае уменьшается с ростом концентрации реагента.
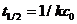 (7.17)
(7.17)
Измерения константы скорости для реакций третьего порядка производиться по формуле:
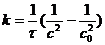
Молекулярность химической реакции
Молекулярность химической реакции - число частиц реагентов, взаимодействующих друг с другом в одной элементарной (простой) реакции и превращающихся в продукты. Так, для реакций в растворах молекулярность реакции не учитывает число молекул растворителя, образующих сольватную оболочку или молекулярные комплексы с реагентами, т. к. эти молекулы не входят в состав продуктов реакции. В р-циях замещения и элиминирования орг. соед., протекающих часто в неск. стадий, М. р. оценивается как число молекул, претерпевающих хим. превращение в лимитирующей стадии. Соответственно числу реагирующих частиц различают мономолекулярные реакции, бимолекулярные реакции и тримолекулярные реакции, отличающиеся кинетическими закономерностями и механизмом. Как правило, молекулярность простой реакции совпадает с порядком реакции, однако бывают и несовпадения. Напр., рекомбинации атомов в газовой фазе протекают через тройные столкновения типа:
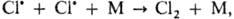
где М - третья частица. Суммарный порядок таких реакций - третий (скорость u = = k[М][Сl]2, где k-константа скорости), но молекулярность равна 2, т.к. в хим. взаимодействии участвуют два атома хлора, а частица М лишь принимает на себя энергию, выделившуюся при рекомбинации атомов, не претерпевая при этом хим. превращения.
Методы определения порядка реакции
Проведение реакции в условиях, когда концентрация одного из реагентов много меньше концентрации другого (других) и скорость реакции зависит от концентрации только этого реагента, используется для определения частных порядков реакции – это т.н. метод избыточных концентраций или метод изолирования Оствальда. Порядок реакции по данному веществу определяется одним из перечисленных ниже методов.
Графический
метод заключается в построении графика зависимости концентрации реагента от
времени в различных координатах. Для различных частных порядков эти зависимости
имеют следующий вид:
|
Порядок реакции |
Зависимость концентрации от времени |
|
1 |
|
|
2 |
|
|
3 |
|
Если построить графики этих зависимостей на основании опытных данных, то лишь одна из них будет являться прямой линией. Если, например, график, построенный по опытным данным, оказался прямолинейным к координатах lnC = f(t), то частный порядок реакции по данному веществу равен единице.
Метод
подбора кинетического уравнения заключается в подстановке экспериментальных
данных изучения зависимости концентрации вещества от времени в кинетические
уравнения различных порядков. Подставляя в приведённые в таблице уравнения
значения концентрации реагента в разные моменты времени, вычисляют значения
константы скорости. Частный порядок реакции по данному веществу равен порядку
того кинетического уравнения, для которого величина константы скорости остаётся
постоянной во времени.
|
Порядок реакции |
Выражение для константы скорости |
|
1 |
|
|
2 |
|
|
3 |
|
Метод
определения времени полупревращения заключается в определении t1/2
для нескольких начальных концентраций. Как видно из приведённых в таблице
уравнений, для реакции первого порядка время полупревращения не зависит от Co,
для реакции второго порядка – обратно пропорционально Co, и
для реакции третьего порядка – обратно пропорционально квадрату начальной
концентрации.
|
Порядок реакции |
Выражение для периода полупревращения |
|
1 |
|
|
2 |
|
|
3 |
|
По характеру зависимости t1/2 от Co нетрудно сделать вывод о порядке реакции по данному веществу. Данный метод, в отличие от описанных выше, применим и для определения дробных порядков.
Таким образом, характер изменения концентрации реагента во времени, период полураспада и единица измерения константы скорости реакции зависят от порядка реакции.
Влияние температуры на скорость реакции
Правило Вант-Гоффа.
Повышение температуры ускоряет большинство химических реакций. Согласно правилу Вант-Гоффа при повышении температуры на 10 К скорость многих реакций увеличивается в 2-4 раза
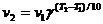 (7.26)
(7.26)
v2 и v1 скорости реакций при температурах Т2 и Т1, Y коэффициент, значение которого для эндотермической реакции выше, чем для экзотермической реакции. Для многих реакций Y лежит в пределах 2-4.
Уравнение (7.26) можно использовать лишь для ориентировочных расчётов, так как их точность не очень высока.
Уравнение Аррениуса.
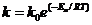 (7.27)
(7.27)
k - константа скорости реакции
k - предэкспоненциальный множитель
e - основание натурального логарифма
E - постоянная, называемая энергией активации, определяемая природой реакции. Значения Ea для химических реакций лежат в пределах 40-400 кДж/моль.
Если при изменении температуры концентрация реагентаостаёся постоянной, то зависимость скорости реакции от температуры описываеться уравнением:
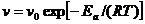
Где Ea =0, Vo=V
Уравнение (7.27) можно представить в виде
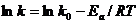 (7.28)
(7.28)
или
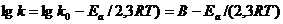 (7.28б)
(7.28б)
Графическое изображение уравнения (7.28б) приведено на рис 7.2.

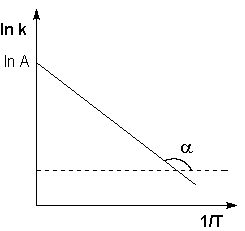
(рис 7.2 зависимость логарифма константы скорости от обратной температуры по уравнению аррениуса)
Как видно из уравнения (7.28б) и рис (7.2)
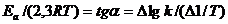
Уравнение Аррениуса озволяет проводить более точные расчеты изменения скорости реакции с увеличением температуры, чем уравнение (7.26). Приведём уравнение Аррениуса для двух температур:
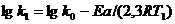
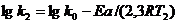
Вычитая из второго уравнения первое, получаем
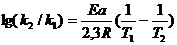 (7.29а)
(7.29а)
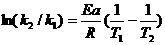 (7.29б)
(7.29б)
По уравнениям (7.29аб) можно рассчитать отношение констант скоростей реакции при двух температурах, если известно Ea, или энергию активации, если известно соотношение констант скоростей реакции при двух температурах.
Аналогичное уравнение можно вывести и из скоростей реакции:
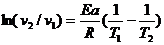 (7.30)
(7.30)
Из уравнений (7.26) и (7.29) следует,
что 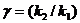 и
и 
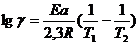
Итак, константа скорости реакции ( а при постоянных концентрациях и скороть реакции) возрастает с увеличением температуры по экспоненциальному закону. В соответсвии с уравнением Аррениуса константа скорости реакции уменьшаеться с ростом энергии активации. Из уравнения Аррениуса также следуе, что чем выше энергия активации, тем выше градиент скорости реакции по температуре. Уравнение Аррениуса позволяет рассчитывать константы скорости (и скорости) реакции при различных температурах.
Энергия активации
В ходе химической реакции разрушаются одни и возникают другие молекулы и соединения, происходит изменение химических связей, т.е. перераспределение электронной плотности. Если бы старые химические связи в ходе реакции сразу полностью разрушались, то на это потребовалось бы большое количество энергии и реакция протекала крайне медленно. Как показали исследования, в ходе реакции система проходит через переходное однородное состояние через образование, так называемого, активированного комплекса.
Например: AB+DC=AD+BC можно представить как:
A-B A…B A B
+ -> . . -> | |
D-C C…D D C
исх в-во акт.комп. прод. р-ии
В активированном комплексе старые связи еще не разрушены, но ослаблены, новые связи наметились, но не образованны. В результате образуется либо новое вещество, либо исходное. Система в переходном состоянии имеет более высокую энергию, чем в исходном и конечном состояниях.
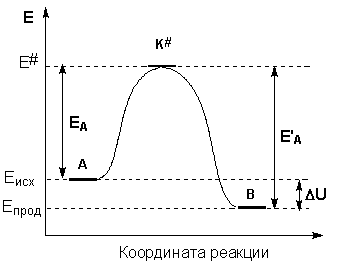
(рис 7.3) энерг. диаграмма хода реакции
Энергия необходимая для перехода вещества в состояние активного комплекса - энергия активации.
Возможность образования активированного комплекса, а соответственно и химического взаимодействия определяется энергией молекул. Как видно из рис 7.4, с увеличением температуры растет и доля молекул способных к активным столкновениям с образованием активированного комплекса, т.е. происходит ускорение реакции.
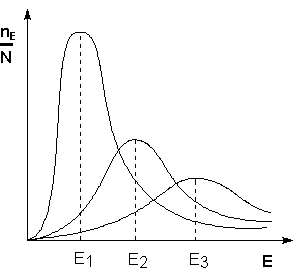
(рис 7.4) Кинетическая энергия молекул
Экзотермические реакции протекают с
меньшей энергией активации, чем эндотермические (см. рис. 7.3.). Высокая
энергия активации является причиной того, что многие химические реакции при не
высоких температурах не протекают, хотя возможны (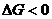
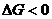
Раздел химии, изучающий реакции в низкотемпературной плазме, получил название плазмохимии, а изучающий химические реакции в сверхнизких температурах - криптохимии.
Итак, энергия активации - это энергия необходимая для перехода частиц в состояние активированного комплекса. С ростом температуры растёт доля этих частиц и скорость реакции. С увеличением энергии активации уменьшается доля активных молекул и скорость реакции.
Химическое равновесие
При некоторой температуре
энтальпийный и энтропийный факторы уравниваются, т.е. 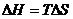 в этом случае
выполняется уравнение:
в этом случае
выполняется уравнение:
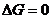 (5.17)
(5.17)
которое является термодинамическим уравнением химического равновесия. В условиях химического равновесия концентрации (или парциальное давление для газов) исходных веществ и продуктов реакции не изменяеться со временем и называются равновесными концентрациями.
Константа химического равновесия.
при равновесной химической реакции:
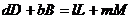
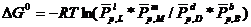 (5.22)
(5.22)
или
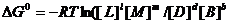 (5.23)
(5.23)
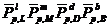 равновесные
относительные
равновесные
относительные
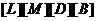 равновесные
концентрации соответствующих веществ
равновесные
концентрации соответствующих веществ
l,m,d,b- показатели степени, равные стехиометрическим коэффициентам.
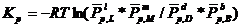 (5.24)
(5.24)
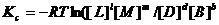 (5.25)
(5.25)
Закон действующих масс: отношение произведения равновесных концентраций продуктов реакции в степенях, равных стехиометрическим коэффициентам, к произведению равновесных концентрация исходных веществ в степенях, равных стехиометрическим коэффициентам, при T=const, является величиной постоянной.
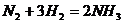
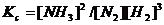
или
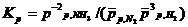
для газов
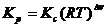 (5.26)
(5.26)
подставляя константу равновесия:
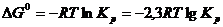 (5.27)
(5.27)
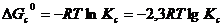 (5.28)
(5.28)
При 298 К 
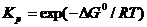 (5.29)
(5.29)
Константа химического равновесия может быть определенна если известно стандартное значение энергии Гиббса.
Принцип Ле Шетелье:
Если на систему, находящуюся в равновесии, оказываеться внешнее воздействие, то равновесие смещается в таком направлении, которое
ослабляет внешнее воздействие.
Например увеличение температуры
вызывает смещение равновесия рассматриваемой реакции получения водорода 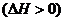 в правую
сторону, а для экзотермической реакции:
в правую
сторону, а для экзотермической реакции:
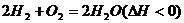
в левую.
Итак, принцип Ле Шетелье позволяет прогнозировать влияние внешних воздействий на смещение равновесия.
Знание законов химической термодинамики позволяет рассчитывать энергетические эффекты химических реакций и фазовых превращений, предсказывать возможность или невозможность протекания химических процессов, а также находить условия химического, фазового и адсорбционного равновесий, и равновесные концентрации реагирующих веществ.
Заключение
В заключение еще раз определим понятие химической кинетика, как науки. Химическая кинетика (от греч. кинетикос – движущий) - наука о механизмах химических реакций и закономерностях их протекания во времени.
В 19 в. результате развития основ
химической термодинамики химики научились рассчитывать состав равновесной смеси
для обратимых химических реакций. Кроме того, на основании несложных расчетов
можно было, не проводя экспериментов, сделать вывод о принципиальной
возможности или невозможности протекания конкретной реакции в данных условиях.
Однако «принципиальная возможность» реакции еще не означает, что она пойдет.
Например, реакция С + О2 = СО2 с точки зрения термодинамики весьма
благоприятна, во всяком случае, при температурах ниже 1000° С (при более
высоких температурах происходит уже распад молекул СО2), т.е. углерод и
кислород должны (практически со 100%-ным выходом) превратиться в диоксид
углерода. Однако опыт показывает, что кусок угля может годами лежать на
воздухе, при свободном доступе кислорода, не претерпевая никаких изменений. То
же можно сказать и о множестве других известных реакций. Например, смеси
водорода с хлором или с кислородом могут сохраняться очень долго без всяких
признаков химических реакций, хотя в обоих случаях реакции термодинамически
благоприятны. Это означает, что после достижения равновесия в стехиометрической
смеси H2 + Cl2 должен остаться только хлороводород, а в смеси 2Н2 + О2 – только
вода. Другой пример: газообразный ацетилен вполне стабилен, хотя реакция C2H2 =
Термодинамически разрешенные реакции, подобные рассмотренным, могут пойти только в определенных условиях. Например, после поджигания уголь или сера самопроизвольно соединяются с кислородом; водород легко реагирует с хлором при повышении температуры или при действии ультрафиолетового света; смесь водорода с кислородом (гремучий газ) взрывается при поджигании или при внесении катализатора. Почему же для осуществления всех этих реакций необходимы специальные воздействия – нагревание, облучение, действие катализаторов? Химическая термодинамика не дает ответа на этот вопрос – понятие времени в ней отсутствует. В то же время для практических целей очень важно знать, пройдет ли данная реакция за секунду, за год или же за многие тысячелетия.
Опыт показывает, что скорость разных реакций может отличаться очень сильно. Практически мгновенно идут многие реакции в водных растворах. Так, при добавлении избытка кислоты к щелочному раствору фенолфталеина малинового цвета раствор мгновенно обесцвечивается, это означает, что реакция нейтрализации, а также реакция превращения окрашенной формы индикатора в бесцветную идут очень быстро. Значительно медленнее идет реакция окисления водного раствора иодида калия кислородом воздуха: желтая окраска продукта реакции – иода появляется лишь через продолжительное время. Медленно протекают процессы коррозии железных и особенно медных сплавов, многие другие процессы.
Предсказание скорости химической реакции, а также выяснение зависимости этой скорости от условий проведения реакции – одна из важных задач химической кинетики – науки, изучающей закономерности протекания реакций во времени. Не менее важна и вторая задача, стоящая перед химической кинетикой – изучение механизма химических реакций, то есть детального пути превращения исходных веществ в продукты реакции.
Список литературы:
1. Ахметов Н.С. Неорганическая химия;
2. Карапетьянц М.Х. Дракин С.И. Общая и неорганическая химия;
3. Коттон Ф. Уилкинсон Дж. Современная неорганическая химия, том 2;
4. Реми Г. Курс неорганической химии, том
5. Общая химия./Под редакцией Соколовской Е.М. и Гузея Л.С.
6. Химический энциклопедический словарь под редакцией И.Л. Кнунянца;
7. Химическая энциклопедия.
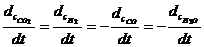 .
.