Интегрирование линейных неоднородных уравнений второго порядка с постоянными коэффициентами. Вынужденные колебания материальной точки
| Примечание | от редактора: автор не назваля себя |
| Загрузить архив: | |
| Файл: ref-26966.zip (504kb [zip], Скачиваний: 252) скачать |



Выполнила:
Проверила:.
Содержание. PAGEREF _Toc169020975 h 2
Введение. PAGEREF _Toc169020976 h 3
Основные понятия и определения. PAGEREF _Toc169020977 h 5
Глава I Интегрирование линейных однородных дифференциальных уравнений. PAGEREF _Toc169020978 h 9
§1.1 Свойства линейного оператора. PAGEREF _Toc169020979 h 9
§1.2 Линейные однородное дифференциальные уравнения второго порядка. PAGEREF _Toc169020980 h 11
1.3.1 Предварительные замечания. PAGEREF _Toc169020982 h 15
1.3.2 Случай различных корней характеристического уравнения. PAGEREF _Toc169020983 h 15
1.3.3 Случай кратных корней характеристического уравнения. PAGEREF _Toc169020984 h 20
§2.3 Метод неопределенных коэффициентов. PAGEREF _Toc169020989 h 32
Глава III Вынужденные колебания материальной точки. PAGEREF _Toc169020990 h 38
§3.2 Свободные колебания. PAGEREF _Toc169020992 h 39
§3.3 Вынужденные колебания. PAGEREF _Toc169020993 h 45
§3.4 Явление резонанса. PAGEREF _Toc169020994 h 47
Глава IV Применение явления резонанса. PAGEREF _Toc169020995 h 51
§4.1 Учет и использование резонанса. PAGEREF _Toc169020996 h 51
§4.3 Дифференциальное уравнение цепной линии. PAGEREF _Toc169020998 h 59
Заключение. PAGEREF _Toc169020999 h 67
Список литературы.. PAGEREF _Toc169021000 h 68
Введение
В математике дифференциальные уравнения занимают особое место. Математическое исследование самых разнообразных явлений, происходящих в природе, часто приводит к решению таких уравнений, поскольку сами законы, которым подчиняется то или иное явление, записывается в виде дифференциальных уравнений.
Задача интегрирования дифференциальных уравнений является классической и важнейшей задачей математического анализа.
Предметом исследования моей дипломной работы являются вынужденные колебания материальной точки, которые задаются неоднородным линейным уравнением второго порядка с постоянными коэффициентами. Проинтегрировав это уравнение, получим закон движения материальной точки. Рассмотрен также частный случай уравнения вынужденный колебаний, т.е. когда частота возмущающей силы совпадает с частотой собственных колебаний - явление резонанса. Так же мною было изучено применение явления резонанса в технике, строительстве, производстве и т.д. Рассмотрены случаи, когда явление резонанса приводило к разрушениям.
Мы живем в мире колебаний. Маятник стенных часов, фундамент быстроходной турбины, кузов железнодорожного вагона, струна гитары и т.д.
По современным воззрениям, все звуковые, тепловые, световые, электрические и магнитные явления, т.е. важнейшие физические процессы окружающего нас мира, сводятся к различным формам колебания материи.
Речь, средство общения людей, музыка, способная вызвать у людей сложные эмоции, - физически определяются так же, как и другие звуковые явления, колебаниями струн, воздуха, пластин и других упругих тел.
Колебания играют важную роль в таких ведущих областях техники, как электричество и радио. Выработка, передача и потребление электрической энергии, телефония, радиовещание, телевидение, радиолокация – все эти важные отрасли основаны на использовании электрических и электромагнитных колебаний.
С колебаниями мы встречаемся и в живом организме. Биение сердца, сокращение желудка, деятельность кишечника имеют колебательный характер.
Строители и механики имеют дело с колебаниями сооружений и машин. Кораблестроители – с качкой и вибрацией корабля и т. д.
Резкое возрастание амплитуды вынужденных колебаний при совпадении собственной частоты и частоты вынуждающей силы называется резонансом.
Резонанс возникает из-за того, что внешняя сила, действуя в такт со свободными колебаниями тела, все время совершает положительную работу. За счет этой работы энергия колеблющегося тела увеличивается и амплитуда колебаний возрастает.
Явление резонанса может играть как полезную, так и вредную роль.
На применении резонанса основано действие язычкового частотометра. Заметив, какая пластина вошла в резонанс, мы определим частоту системы. Маленький ребенок может раскачать язык большого колокола, если будет действовать на веревку в такт со свободными колебаниями языка.
С резонансом можно встретиться и тогда, когда это совсем нежелательно. Так, например, в 1750 году близ города Анжера во Франции через цепной мост длиной 102 м шел в ногу отряд солдат. Частота их шагов совпала с частотой свободных колебаний моста. Из-за этого размахи колебаний моста резко увеличились, и цепи оборвались. Мост обрушился в реку. В 1830 году по той же причине обрушился подвесной мост около Манчестера в Англии, когда по нему маршировал военный отряд. В 1906 году из-за резонанса разрушился и так называемый Египетский мост в Петербурге, по которому проходил кавалерийский эскадрон. Теперь для предотвращения подобных случаев войсковым частям приказывают “сбить ногу” и идти не строевым, а вольным шагом.
Чтобы избежать резонанса при переезде поезда через мост, он проходит его либо на медленном ходу, либо на максимальной скорости (чтобы частота ударов колес о стыки рельсов не оказалась равной собственной частоте моста).
При отборе материала для дипломной работы я старалась изложить основные
идеи и методы, применяемые для изучения линейных неоднородных дифференциальных
уравнений второго порядка с постоянными коэффициентами. Уравнения такого типа
являются предметом внимательного изучения ученых, так как к ним приводится
большое количество задач механики и других наук. Они особенно просты по своей
природе и вместе с тем важны по своим приложениям. Они имеют значение в важном
вопросе о малых колебаниях, так как было показано выше, что линейные
неоднородные дифференциальные уравнения второго порядка с постоянными
коэффициентами описывают процесс колебаний, так как мы живем в «мире
колебаний».
Основные понятия и определения
В настоящей дипломной работе применены следующие термины с соответствующими определениями.
Дифференциальные уравнения – это уравнения, в которые неизвестная функция входит под знаком производной. Основная задача теории дифференциальных уравнений – изучение функций, являющихся решением таких уравнений. Решением дифференциального уравнения называется функция, которая при подстановке в уравнение обращает его в тождество.
Дифференциальные уравнения можно разделить на обыкновенные дифференциальные уравнения, в которых неизвестные функции являются функциями одной переменной, и на дифференциальные уравнения в частных производных, в которых неизвестные функции являются функциями двух и большего числа переменных.
Наивысший порядок производной, входящей в дифференциальное уравнение, называется порядком этого уравнения.
Процесс отыскания решения дифференциального уравнения называется его интегрированием, а график решения дифференциального уравнения – интегральной кривой.
Дифференциальные уравнения первого порядка
Дифференциальное уравнение первого порядка в общем случае можно записать в виде
 (1)
(1)
Уравнение связывает независимую
переменную x, искомую функцию y и ее производную 

 (2)
(2)
и называют дифференциальным уравнение первого порядка, разрешенным относительно производной.
Уравнение (2) устанавливает связь
между координатами точки  и угловым
коэффициентом
и угловым
коэффициентом  касательной к
интегральной кривой, проходящей через эту точку. Следовательно,
дифференциальное уравнение
касательной к
интегральной кривой, проходящей через эту точку. Следовательно,
дифференциальное уравнение  дает совокупность
направлений (поле направлений) на плоскости Oxy. Таково геометрическое истолкование
дифференциального уравнения первого порядка.
дает совокупность
направлений (поле направлений) на плоскости Oxy. Таково геометрическое истолкование
дифференциального уравнения первого порядка.
Дифференциальное уравнение первого порядка, разрешимое относительно производной, можно записать в дифференциальной форме:
 (3)
(3)
где  и
и  - известные функции.
Уравнение (3) удобно тем, что переменные x
и y в нем равноправны, т.е. любую из
них можно рассматривать как функцию другой. Отметим, что от одного вида записи
дифференциального уравнения можно перейти к другому.
- известные функции.
Уравнение (3) удобно тем, что переменные x
и y в нем равноправны, т.е. любую из
них можно рассматривать как функцию другой. Отметим, что от одного вида записи
дифференциального уравнения можно перейти к другому.
Чтобы решение дифференциального уравнения приобрело конкретный смысл, его надо подчинить некоторым дополнительным условиям.
Условие, что при  функция y должна быть равна заданному числу
функция y должна быть равна заданному числу 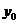
 называется начальным условием. Начальное условие
записывается в виде
называется начальным условием. Начальное условие
записывается в виде
 или
или  (4)
(4)
Общим решением дифференциального уравнения первого
порядка называется функция 
1. Функция  является решением
дифференциального уравнения при каждом фиксированном значении c.
является решением
дифференциального уравнения при каждом фиксированном значении c.
2. Каково бы ни было начальное условие
(4), можно найти такое значение постоянной 
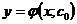 удовлетворяет данному
начальному условию.
удовлетворяет данному
начальному условию.
Частным решением дифференциального уравнения первого
порядка называется любая функция 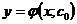
 при конкретном
значении постоянной
при конкретном
значении постоянной 
Задача отыскания решения дифференциального уравнения первого порядка (3), удовлетворяющего заданному начальному условию (4), называется задачей Коши.
Теорема (существования и единственности
задачи Коши). Если в уравнении (2) функция  и ее частная
производная
и ее частная
производная  непрерывны в некоторой
области D, содержащей точку
непрерывны в некоторой
области D, содержащей точку 
 этого уравнения,
удовлетворяющее начальному условию (4).
этого уравнения,
удовлетворяющее начальному условию (4).
Дифференциальные уравнения высших порядков
Дифференциальные уравнения порядка выше первого называются дифференциальными уравнениями высших порядков. Дифференциальное уравнение второго порядка в общем случае запишется в виде
 (5)
(5)
или, если это возможно, в виде, разрешенном относительно старшей производной:
 (6)
(6)
Решением дифференциального уравнения
(6) называется всякая функция вида 
Общим решением дифференциального уравнения
называется функция вида 
 и
и  - не зависящее от x произвольные постоянные,
удовлетворяющая условиям:
- не зависящее от x произвольные постоянные,
удовлетворяющая условиям:
1.  является решением
дифференциального уравнения для каждого фиксированного значения
является решением
дифференциального уравнения для каждого фиксированного значения  и
и 
2. Каковы бы ни были начальные условия

 (7)
(7)
существуют единственные значения
постоянных  и
и  такие, что функция
такие, что функция  является решением
уравнения (6) и удовлетворяет начальным условиям (7).
является решением
уравнения (6) и удовлетворяет начальным условиям (7).
Всякое решение  уравнения (6),
получающееся из общего решения
уравнения (6),
получающееся из общего решения  при конкретных
значениях постоянных
при конкретных
значениях постоянных  и
и  частным
решением.
частным
решением.
Как и в случае уравнения первого порядка, задача нахождения решения дифференциального уравнения, удовлетворяющего заданным начальным условиям (7), называется задачей Коши.
Теорема (существования и единственности
задачи Коши). Если в уравнении (6) функция  и ее частные
производные
и ее частные
производные  и
и  непрерывны в некоторой
области D изменения переменных x, y и
непрерывны в некоторой
области D изменения переменных x, y и 
 существует
единственное решение
существует
единственное решение  уравнения (6),
удовлетворяющее начальным условиям (7).
уравнения (6),
удовлетворяющее начальным условиям (7).
Аналогичные понятия и определения
имеют место и для дифференциального уравнения  порядка, которое в
общем виде записывается как
порядка, которое в
общем виде записывается как

Нам часто будут встречаться функции
вещественного переменного t, называемого временем. Производная
по t называется скоростью и обозначается
чаще всего точкой наверху:  t называется ускорением и
обозначается:
t называется ускорением и
обозначается: 
Глава
I
Интегрирование линейных однородных дифференциальных уравнений
§1.1 Свойства линейного оператора
Линейное уравнение  порядка имеет следующий
общий вид:
порядка имеет следующий
общий вид:
 (1.1.1)
(1.1.1)
Если в рассматриваемом интервале
изменения x функция  тождественно равна
нулю, то уравнение (1.1.1) принимает вид
тождественно равна
нулю, то уравнение (1.1.1) принимает вид
 (1.1.2)
(1.1.2)
и называется однородным. Если  неоднородным.
неоднородным.
Будем предполагать, что функции 
 - непрерывны на
интервале
- непрерывны на
интервале 
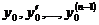 при любом
при любом 
 будет только очевидное
нулевое решение y = 0.
будет только очевидное
нулевое решение y = 0.
Для упрощения дальнейшего изложения
обозначим левую часть линейного уравнения (1.1.1) через 
 (1.1.3)
(1.1.3)
Таким образом  есть результат
выполнения над функцией y операций,
указанных в правой части формулы (1.1.3), а именно: вычисление производных от
функции y вплоть до
порядка n включительно,
умножение
есть результат
выполнения над функцией y операций,
указанных в правой части формулы (1.1.3), а именно: вычисление производных от
функции y вплоть до
порядка n включительно,
умножение  на заданные функции
на заданные функции 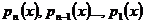 L:
L:

и будем называть его линейным
дифференциальным оператором  . В частности, линейный дифференциальный
оператор второго порядка имеет вид
. В частности, линейный дифференциальный
оператор второго порядка имеет вид

Пример 1. Рассмотрим оператор

Вычислим 
 и
и 

Линейный дифференциальный оператор L обладает следующими основными свойствами (линейность оператора L):
1) постоянный множитель можно выносить знак оператора

2) оператор от суммы двух функций равен сумме операторов от этих функций

В справедливости этих свойств легко убедиться непосредственной проверкой. В самом деле, имеем





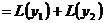
Из этих основных свойств оператора L следует, что

т.е. оператор от линейной комбинации m функций равен линейной комбинации операторов от этих функций.
Используя оператор L, можно записать неоднородное и однородное линейные уравнения (1.1.1) и (1.1.2) соответственно в виде
 (1.1.4)
(1.1.4)
и
 (1.1.5)
(1.1.5)
Если функция  является решением
уравнения (1.1.4) или (1.1.5) в некотором интервале
является решением
уравнения (1.1.4) или (1.1.5) в некотором интервале  L от этой функции равно
L от этой функции равно  или нулю при всех x из
или нулю при всех x из 


или


§1.2 Линейные однородное дифференциальные уравнения второго порядка
Рассмотрим линейное однородное дифференциальное уравнение второго порядка
 (1.2.1)
(1.2.1)
и установим некоторые свойства его решений.
Теорема 1. Если функции  и
и  являются частными
решениями уравнения (1.2.1), то решением этого уравнения является также функция
являются частными
решениями уравнения (1.2.1), то решением этого уравнения является также функция
 (1.2.2)
(1.2.2)
где  и
и  - произвольные
постоянные.
- произвольные
постоянные.
Подставим функцию  и ее производные в
левую часть линейного однородного уравнения (1.2.1). Получаем:
и ее производные в
левую часть линейного однородного уравнения (1.2.1). Получаем:



так как функции  и
и  - решения уравнения
(1.2.1) и, значит, выражения в скобках тождественно равны нулю.
- решения уравнения
(1.2.1) и, значит, выражения в скобках тождественно равны нулю.
Таким образом, функция (1.2.2) также является решением уравнения (1.2.1).
Из
теоремы 1, как следствие, вытекает, что если  и
и  - решения уравнения
(1.2.1), то решениями его будут также функции
- решения уравнения
(1.2.1), то решениями его будут также функции  и
и 
Функция (1.2.2) содержит две произвольные постоянные и является решением уравнения (1.2.1). Может ли она являться общим решением уравнения (1.2.1)? Для ответа на вопрос введем понятие линейной зависимости и линейной независимости функций.
Функции  и
и  называются линейно
независимыми на интервале
называются линейно
независимыми на интервале 
 (1.2.3)
(1.2.3)
где 

Если хотя бы одно из
чисел  или
или  отлично от нуля и
выполняется равенство (1.2.3), то функции
отлично от нуля и
выполняется равенство (1.2.3), то функции  и
и  называются линейно
зависимыми на
называются линейно
зависимыми на 
Очевидно, что функции  и
и  линейно зависимы тогда
и только тогда, когда они пропорциональны, т.е. для всех
линейно зависимы тогда
и только тогда, когда они пропорциональны, т.е. для всех  выполняется равенство
выполняется равенство 

Например, функции  и
и  линейно зависимы:
линейно зависимы: 
 и
и  - линейно независимы:
- линейно независимы: 
 и
и  являются линейно
независимыми: равенство
являются линейно
независимыми: равенство  выполняется для всех
выполняется для всех  лишь при
лишь при  (или
(или 
Средством изучения линейной зависимости системы функций является определитель Вронского или вронскиан.
Для двух дифференцируемых
функций  и
и  вронскиан имеет вид
вронскиан имеет вид

Имеют место следующие теоремы.
Теорема 2. Если дифференцируемые функции  и
и  линейно зависимы на
линейно зависимы на 
Так как функции  и
и  линейно зависимы, то в
равенстве (1.2.3) значение
линейно зависимы, то в
равенстве (1.2.3) значение  и
и  отлично от нуля. Пусть
отлично от нуля. Пусть




Теорема 3. Если функции  и
и  - линейно независимые
решения уравнения (1.2.1) на
- линейно независимые
решения уравнения (1.2.1) на 
Из теорем 2 и 3 следует,
что вронскиан не равен нулю ни в одной
точке интервала  тогда и только тогда,
когда частные решения линейно независимы.
тогда и только тогда,
когда частные решения линейно независимы.
Совокупность любых двух
линейно независимых на интервале  частных решений
частных решений  и
и  линейного однородного
дифференциального уравнения второго порядка определяет фундаментальную систему
решений этого уравнения: любое произвольное решение может быть получено как
комбинация
линейного однородного
дифференциального уравнения второго порядка определяет фундаментальную систему
решений этого уравнения: любое произвольное решение может быть получено как
комбинация 
Теперь можно сказать, при каких условиях функция (1.2.2) будет общим решением уравнения (1.2.1).
Теорема 4. (структура
общего решения). Если два частных решения  и
и  линейного однородного
дифференциального уравнения (1.2.1) образуют на интервале
линейного однородного
дифференциального уравнения (1.2.1) образуют на интервале  фундаментальную
систему, то общим решением этого уравнения является функция
фундаментальную
систему, то общим решением этого уравнения является функция
 (1.2.4)
(1.2.4)
где  и
и  - произвольные
постоянные.
- произвольные
постоянные.
Согласно теореме 1, функция (1.2.4) является решением уравнения (1.2.1). Остается доказать, что это решение общее, т.е. что из него можно выделить единственное частное решение, удовлетворяющее заданным начальным условиям

 (1.2.5)
(1.2.5)
где 
Подставив начальные условия (1.2.5) в решение (1.2.2), получим систему уравнений

где  и
и 
Так как решения  и
и  образуют
фундаментальную систему решений на
образуют
фундаментальную систему решений на  и
и 



Решение  является частным
решением (единственным, в силу теоремы единственности) уравнения (1.2.1),
удовлетворяющим начальным условиям (1.2.5).
является частным
решением (единственным, в силу теоремы единственности) уравнения (1.2.1),
удовлетворяющим начальным условиям (1.2.5).
Теорема доказана.
§1.3 Интегрирование однородного линейного уравнения второго порядка с постоянными коэффициентами методом Эйлера
1.3.1 Предварительные замечания
Рассмотрим линейное уравнение n-ого порядка
 (1.3.1)
(1.3.1)
где коэффициенты  суть вещественные
числа, а правая часть
суть вещественные
числа, а правая часть  непрерывна в некотором
интервале
непрерывна в некотором
интервале 

Так как интегрирование неоднородного линейного уравнения приводится к интегрированию соответствующего однородного уравнения, то рассмотрим сначала вопрос о построении общего решения однородного уравнения
 (1.3.2)
(1.3.2)
Для нахождения общего решения этого уравнения достаточно знать фундаментальную систему решений. Так как коэффициенты уравнения постоянны и, следовательно, заведомо непрерывны при всех значениях x, то согласно теореме Пикара и все решения уравнения (1.3.2) определены при всех значениях x. Поэтому в дальнейшем мы не будем указывать ни интервал существования частных решений, ни область общего решения.
Эйлер доказал, что для однородного линейного уравнения с постоянными коэффициентами всегда можно построить фундаментальную систему решений, состоящую из элементарных функций, и, следовательно, это уравнение всегда интегрируется в элементарных функциях.
1.3.2 Случай различных корней характеристического уравнения
Частным случаем линейных однородных дифференциальных уравнений являются линейные однородные дифференциальные уравнения с постоянными коэффициентами.
Пусть дано линейное однородное дифференциальное уравнение второго порядка
 (1.3.3)
(1.3.3)
где  и
и  - вещественные числа.
Будем, следуя Эйлеру, искать частное решение уравнения (1.3.3) в виде
- вещественные числа.
Будем, следуя Эйлеру, искать частное решение уравнения (1.3.3) в виде
 (1.3.4)
(1.3.4)
где  - подлежащее
определению число (вещественное или комплексное). Согласно определению решения
функции (1.3.4) будет решением уравнения (1.3.3), если
- подлежащее
определению число (вещественное или комплексное). Согласно определению решения
функции (1.3.4) будет решением уравнения (1.3.3), если  выбрано так, что
функция (1.3.4) обращает это уравнение в тождество
выбрано так, что
функция (1.3.4) обращает это уравнение в тождество
 (1.3.5)
(1.3.5)
Вычисляя 
 (1.3.6)
(1.3.6)
будем иметь

так что
 (1.3.7)
(1.3.7)
или

где

Из (1.3.7) следует, что
интересующее нас тождество (1.3.5) будет выполнятся тогда и только тогда, когда

 является корнем
уравнения
является корнем
уравнения
 (1.3.8)
(1.3.8)
Это уравнение называется характеристическим уравнением, а его корни – характеристическими числами уравнения (1.3.3).
Заметим, что
характеристическое уравнение (1.3.8) может быть составлено по данному
дифференциальному уравнению (1.3.3) заменой 
 и
и  на
на 
 и 1, т.е. степень
и 1, т.е. степень  совпадает с порядком
производной, если условиться считать, что производная нулевого порядка от
функции есть сама функция
совпадает с порядком
производной, если условиться считать, что производная нулевого порядка от
функции есть сама функция 
Структура фундаментальной системы решений, а вместе с ней и общего решения уравнения (1.3.3) зависит от вида корней характеристического уравнения (1.3.8).
Рассмотрим сначала
случаи, когда эти корни различные и вещественные. Обозначим их через  и
и 
 числа
числа  и
и 

 (1.3.9)
(1.3.9)
Эти решения, очевидно, линейно независимы, так как их отношение

не равно тождественно постоянной величине. В линейной независимости решений (1.3.9) можно убедиться также при помощи определителя Вронского. Имеем

Следовательно, частные решения (1.3.9) образуют фундаментальную систему решений. А тогда общим решением уравнения (1.3.3) будет

Пример 1. Рассмотрим уравнение
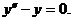
Характеристическим уравнением будет

Его корни 
 (вещественные и
различные). Поэтому фундаментальная система решений имеет вид
(вещественные и
различные). Поэтому фундаментальная система решений имеет вид


а общим решением будет

Пример 2. Пусть дано уравнение

Имеем



Общим решением будет

Предположим теперь, что корни характеристического уравнения комплексные. Так как коэффициенты этого уравнения вещественные, то эти комплексные корни являются сопряженными, так что они имеют вид


Подставляя корень  в формулу (1.3.4),
получим комплексное решение
в формулу (1.3.4),
получим комплексное решение
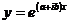 (1.3.10)
(1.3.10)
Но

поэтому решение (1.3.10) можно записать так
 (1.3.11)
(1.3.11)
Отделяя в комплексном решении (1.3.11) вещественную и мнимую части, получим два вещественных частных решения

 (1.3.12)
(1.3.12)
Эти решения независимы, так как
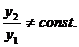
Аналогично убеждаемся,
что сопряженному корню  соответствуют
вещественные частные решения
соответствуют
вещественные частные решения

 (1.3.13)
(1.3.13)
Решения (1.3.13), очевидно, линейно зависимы с решениями (1.3.12).
Таким образом, паре
сопряженных комплексных корней  соответствуют два
вещественных линейно независимых частных решения (1.3.12).
соответствуют два
вещественных линейно независимых частных решения (1.3.12).
Решения (1.3.12) образуют фундаментальную систему решений уравнения (1.3.3). Поэтому

или

будет общим решением уравнения (1.3.3).
Если корни  и
и  чисто мнимые, т.е.
чисто мнимые, т.е. 


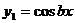
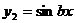 (1.3.14)
(1.3.14)
Эти решения образуют фундаментальную систему решений уравнения (1.3.3), а

есть общее решение этого уравнения.
Пример 3. Рассмотрим уравнение
 (1.3.15)
(1.3.15)
Характеристическое уравнение

имеет сопряженные комплексные корни 


Общим решением будет
 (1.3.16)
(1.3.16)
Заметим, что из формулы общего решения (1.3.16) видно, что все ненулевые решения уравнения (1.3.15) обладают свойством:

Пример 4. Решить уравнение
 (1.3.17)
(1.3.17)
Характеристическое уравнение

имеет чисто мнимые корни 


так что общим решением будет
 (1.3.18)
(1.3.18)
Из формулы общего решения
(1.3.18) видно, что все решения уравнения (1.3.17) ограничены по x на интервале 
1.3.3 Случай кратных корней характеристического уравнения
Предположим теперь, что
характеристическое уравнение (1.3.8) имеет равные корни 
 (1.3.19)
(1.3.19)
или

Убедимся непосредственной подстановкой в уравнение (1.3.3) в том, что
 (1.3.20)
(1.3.20)
есть второе частное решение уравнения (1.3.3), линейно независимое с решением (1.3.19):


Поэтому

(так как 
Общим решением уравнения (1.3.3) будет

Пример 5. Решить уравнение
 (1.3.21)
(1.3.21)
Характеристическое уравнение

имеет равные корни 


Образуют фундаментальную систему решений, а общим решением будет
 (1.3.22)
(1.3.22)
Из формулы общего решения (1.3.22) видно, что все ненулевые решения уравнения (1.3.21) обладают свойством:

§1.4 Система линейно независимых решений (фундамент) и определитель Вронского
Зная n частных решений y1, y2,…,yn, можно построить семейство решений, зависящее от n произвольных постоянных:
 (1.4.1)
(1.4.1)
Это решение, как показано ниже, будет общим решением, если частные решения y1, y2,…,yn обладают одним дополнительным свойством, относящемся к характеру зависимости между ними.
Прежде чем сформулировать это свойство, введем понятие о линейной независимости функций.
Пусть даны  функций от
функций от 

 (1.4.2)
(1.4.2)
Составим их линейную комбинацию с постоянными коэффициентами:

Если эта линейная
комбинация тождественно равна нулю в интервале 


только в очевидном случае, т.е. при
нулевых значениях коэффициентов 

 и
и  линейно независимы в интервале
линейно независимы в интервале 


Пример 1.Функции


линейно независимы в любом интервале. В самом деле, соотношение
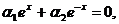
в котором хотя бы одно из чисел  и
и  отличны от нуля, может
выполняться не более чем при одном значении x. Это следует также из того, что
отличны от нуля, может
выполняться не более чем при одном значении x. Это следует также из того, что

Пример 2. Функции


линейно зависимы в любом интервале, ибо

так что 


 есть однородная
линейная функция от
есть однородная
линейная функция от  .
.
Теорема. Если функции (1.4.2) линейно
зависимы в интервале  .
.
Действительно, пусть


где, например, 

т.е.  является линейной
комбинацией функций
является линейной
комбинацией функций 
Совокупности  решений
решений

 (1.4.3)
(1.4.3)
однородного линейного уравнения 




Пример 3. Рассмотрим уравнение

Это однородное линейное уравнение
второго порядка имеет два частных решения  и
и 

Дадим признак линейно
независимости  частных решений
(1.4.3) однородного линейного уравнения
частных решений
(1.4.3) однородного линейного уравнения 
 включительно:
включительно:

Этот определитель
называется определителем Вронского решений 
Теорема. Для того, чтобы решения (1.4.3)
были линейно независимыми в 

 не обращался в нуль ни
в одной точке из
не обращался в нуль ни
в одной точке из 
Необходимость. Пусть
решения (1.4.3) линейно независимы в 


Построим однородную
линейную систему  уравнений
уравнений
 (1.4.4)
(1.4.4)
с неизвестными 


(т.е. хоть одно из чисел  не равно нулю).
не равно нулю).
Построим линейную
комбинацию решений (1.4.3), взяв в качестве коэффициентов числа 
 (1.4.5)
(1.4.5)
Это решение удовлетворяет нулевым начальным условиям
 при
при 
как это видно из системы (1.4.4),
если заменить в ней неизвестные  их значениями,
найденными из этой системы. Следовательно, в силу единственности задачи Коши,
которая имеет место вследствие непрерывности коэффициентов уравнения
их значениями,
найденными из этой системы. Следовательно, в силу единственности задачи Коши,
которая имеет место вследствие непрерывности коэффициентов уравнения  (1.4.5)
должно быть нулевым, т. е.
(1.4.5)
должно быть нулевым, т. е.

 (1.4.6)
(1.4.6)
Так как среди чисел  хоть одно отлично от
нуля, то тождество (1.4.6) означает, что вопреки предположению решения (1.4.4)
линейно зависимы в
хоть одно отлично от
нуля, то тождество (1.4.6) означает, что вопреки предположению решения (1.4.4)
линейно зависимы в 
Достаточность. Предположим,
что  не обращается в нуль в
не обращается в нуль в




где, например,  Тогда
Тогда
 (1.4.7)
(1.4.7)
откуда
 (1.4.8)
(1.4.8)
Заменив теперь элементы
последнего столбца определителя Вронского их значениями из формул (1.4.7) и
(1.4.8). Получим определитель, у которого элементы одного (последнего) столбца
являются линейными комбинациями элементов (всех) других столбцов. Такой
определитель, как известно, равен нулю. Таким образом, вопреки предложению  в
в 
Теорема доказана.
Заметим, что при доказательстве необходимости существенно использовано
предложение о непрерывности коэффициентов уравнения в интервале 
Значение определителя
Вронского  решений однородного
линейного уравнения
решений однородного
линейного уравнения  тесно связано с самим
уравнение, а именно: имеет место следующая формула Остроградского – Лиувилля:
тесно связано с самим
уравнение, а именно: имеет место следующая формула Остроградского – Лиувилля:
 (1.4.9)
(1.4.9)
Из формулы (1.4.9) видно,
что определитель Вронского  решений уравнения
решений уравнения  обладает двумя
замечательными свойствами:
обладает двумя
замечательными свойствами:
1. Если  обращается в нуль в
одной точке из интервала
обращается в нуль в
одной точке из интервала  .
.
2. Если  не равен нулю хотя бы
в одной точке
не равен нулю хотя бы
в одной точке 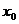 из интервала
из интервала  .
.
Таким образом, для того
чтобы  решений (1.4.3)
составляли фундаментальную систему решений уравнения
решений (1.4.3)
составляли фундаментальную систему решений уравнения  в интервале
в интервале 

В частности решения
уравнения (1.4.3) с начальными условиями 



 образуют фундаментальную систему решений. Такая
фундаментальная система называется нормированной в точке
образуют фундаментальную систему решений. Такая
фундаментальная система называется нормированной в точке 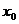
Пример 4. Рассмотрим уравнение

Оно имеет решения  и
и 
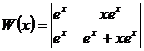

Следовательно, решения  и
и  образуют
фундаментальную систему решений в
образуют
фундаментальную систему решений в 
Глава
II
Интегрирование линейных неоднородных дифференциальных уравнений второго порядка
§2.1 Структура общего решения линейного неоднородного уравнения второго порядка
Рассмотрим линейное неоднородное уравнение второго порядка
 (2.1.1)
(2.1.1)
где 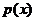

 - заданные,
непрерывные на
- заданные,
непрерывные на  функции. Уравнение
функции. Уравнение
 (2.1.2)
(2.1.2)
левая часть которого совпадает с левой частью линейного неоднородного дифференциального уравнения (2.1.1), называется соответствующим ему однородным уравнением.
Теорема 1. (структура
общего решения). Общим решением y
уравнения (2.1.1) является сумма его произвольного частного решения  и общего решения Y соответствующего однородного уравнения (2.1.2), т.е.
и общего решения Y соответствующего однородного уравнения (2.1.2), т.е.
 (2.1.3)
(2.1.3)
Убедимся, что функция
(2.1.3) – решение уравнения (2.1.1). Так как  есть решение уравнения
(2.1.1), а Y – решение уравнения (2.1.2), то
есть решение уравнения
(2.1.1), а Y – решение уравнения (2.1.2), то
 и
и 
В таком случае имеем:



Это означает, что функция  является решением
уравнения (2.1.1). Покажем теперь, что функция
является решением
уравнения (2.1.1). Покажем теперь, что функция
 (2.1.4)
(2.1.4)
является общим решением уравнения (2.1.1). Для этого надо доказать, что из решения (2.1.4) можно выделить единственное частное решение, удовлетворяющее заданным начальным условиям

 (2.1.5)
(2.1.5)
Продифференцировав функцию (2.1.4) и подставив начальные условия (2.1.5) в функцию (2.1.4) и ее производную, получим систему уравнений:

где 

 и
и 
 для функции
для функции  и
и  в точке
в точке 
 и
и  линейно независимы
(образуют фундаментальную систему решений), т.е.
линейно независимы
(образуют фундаментальную систему решений), т.е. 
 и
и 
Решение  является частным
решением уравнения (2.1.1), удовлетворяющим заданным начальным условиям
(2.1.5).
является частным
решением уравнения (2.1.1), удовлетворяющим заданным начальным условиям
(2.1.5).
Теорема доказана.
Теорема 2. (о наложении решений) Если правая часть уравнения (2.1.1)
представляет собой сумму двух функций: 
 и
и 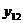 - частные решения
уравнений
- частные решения
уравнений  и
и  соответственно, то
функция
соответственно, то
функция  является решением
данного уравнения.
является решением
данного уравнения.
Действительно, 
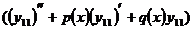

Пример. Рассмотрим уравнение

Для уравнений
 и
и 
легко находятся частные решения. Для
первого из них частным решением будет 

 есть частное решение
уравнения, а его общим решением будет
есть частное решение
уравнения, а его общим решением будет

§2.2 Метод вариации произвольных постоянных (метод Лагранжа) для уравнения второго порядка
Пусть дано неоднородное линейное уравнение второго порядка
 (2.2.1)
(2.2.1)
где коэффициенты 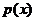
 и правая часть
и правая часть  есть функции от x, непрерывные в некотором интервале
есть функции от x, непрерывные в некотором интервале 
Рассмотрим наряду с уравнением (2.2.1) соответствующее ему однородное уравнение
 (2.2.2)
(2.2.2)
Пусть 
 - фундаментальная
система решений уравнения (2.2.2), так что
- фундаментальная
система решений уравнения (2.2.2), так что

 (2.2.3)
(2.2.3)
и
 (2.2.4)
(2.2.4)
Тогда, как известно, общее решение уравнения (2.2.2) имеет вид
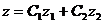
где  и
и  - произвольные
постоянные.
- произвольные
постоянные.
Будем искать решение уравнения (2.2.1) в виде
 (2.2.5)
(2.2.5)
где 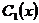 и
и  - некоторые функции от
x, подлежащие определению.
- некоторые функции от
x, подлежащие определению.
Подставляя (2.2.5) в
уравнение (2.2.1), получим одно условие, которому должны удовлетворять две
неизвестные функции 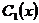 и
и 
 (2.2.6)
(2.2.6)
Оно содержит производные
второго порядка от искомых функций 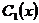 и
и  y мы получили уравнение того же порядка,
но уже с двумя неизвестными функциями -
y мы получили уравнение того же порядка,
но уже с двумя неизвестными функциями - 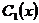 и
и 
Дифференцируя обе части равенства (2.2.5), имеем

Чтобы при вычислении  не появились
производные второго порядка от
не появились
производные второго порядка от 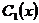 и
и 

Это и есть то
дополнительное условие на искомые функции 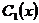 и
и 
 примет вид
примет вид
 (2.2.7)
(2.2.7)
Вычисляя теперь 
 (2.2.8)
(2.2.8)
Подставим выражения для 
 и
и  из формул (2.2.5),
(2.2.7) и (2.2.8) в уравнение (2.2.1).
Для этого умножим левые и правые части этих формул соответственно на
из формул (2.2.5),
(2.2.7) и (2.2.8) в уравнение (2.2.1).
Для этого умножим левые и правые части этих формул соответственно на 
 и 1, сложим почленно и
приравняем сумму правой части уравнения (2.2.1). Получим
и 1, сложим почленно и
приравняем сумму правой части уравнения (2.2.1). Получим

Здесь в силу (2.2.3) первые два слагаемых равны нулю, поэтому

Это и есть новый вид
условия (2.2.6). Теперь оно уже не содержит производных второго порядка от 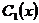 и
и 
Таким образом, мы получили систему дифференциальных уравнений

Эта система в силу
(2.2.4) однозначно разрешим относительно 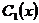 и
и 

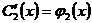
где  и
и  суть вполне
определенные функции от x. Их можно
найти, например, по правилу Крамера. При этом, так как
суть вполне
определенные функции от x. Их можно
найти, например, по правилу Крамера. При этом, так как 

 и
и  непрерывны в интервале
непрерывны в интервале

 и
и  будут непрерывны в
интервале
будут непрерывны в
интервале 


где  и
и  - произвольные
постоянные.
- произвольные
постоянные.
Подставляя найденные
значения функций 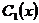 и
и  в формулу (2.2.5),
получим
в формулу (2.2.5),
получим
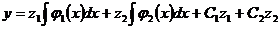 (2.2.9)
(2.2.9)
Полагая здесь 

так что формулу (2.2.9) можно записать в виде

откуда в силу теоремы о том, что
решение неоднородного линейного уравнения равно сумме какого-нибудь частного
решения этого уравнения и общего решения соответствующего однородного
уравнения, следует, что формула (2.2.9) дает общее решение уравнения (2.2.1).
Все решения, входящие в формулу (2.2.9), заведомо определены в интервале 
Пример. Рассмотрим уравнение
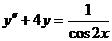 (2.2.10)
(2.2.10)
Здесь первая часть непрерывна в каждом из интервалов
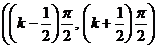
где  - любое целое число.
Соответствующее однородное уравнение
- любое целое число.
Соответствующее однородное уравнение

имеет фундаментальную систему решений


так что общим решением этого
уравнения будет 
Будем искать решение уравнения (2.2.10) в виде
 (2.2.11)
(2.2.11)
Для нахождения 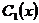 и
и  имеем систему
имеем систему

Решая ее, найдем

Подставляя найденные
значения 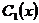 и
и  в формулу (2.2.11),
получим общее решение уравнения (2.2.10) в виде
в формулу (2.2.11),
получим общее решение уравнения (2.2.10) в виде

§2.3 Метод неопределенных коэффициентов
Рассмотрим линейное неоднородное уравнение второго порядка с постоянными коэффициентами
 (2.3.1)
(2.3.1)
где  и
и  - вещественные числа;
- вещественные числа;  - непрерывная функция.
- непрерывная функция.
Как известно, общее
решение такого уравнения представляет собой сумму частного решения
неоднородного уравнения и общего решения соответствующего однородного
уравнения. Частное решение уравнения (2.3.1) может быть найдено методом
вариации произвольных постоянных. Однако если в правой части уравнения (2.3.1)
– многочлен, либо показательная функция, либо тригонометрическая функция  или
или 
Суть метода неопределенных коэффициентов состоит в следующем: по виду
правой части  уравнения (2.3.1)
записывают ожидаемую форму частного решения с неопределенным коэффициентами,
затем подставляют ее уравнение (2.3.1) и из полученного тождества находят
значения коэффициентов.
уравнения (2.3.1)
записывают ожидаемую форму частного решения с неопределенным коэффициентами,
затем подставляют ее уравнение (2.3.1) и из полученного тождества находят
значения коэффициентов.
Рассмотрим различные виды правых частей уравнения (2.3.1):
I. Правая часть имеет вид
 (2.3.2)
(2.3.2)
где  - многочлен степени n.
- многочлен степени n.
Тогда частное решение

где  - многочлен той же
степени, что и
- многочлен той же
степени, что и  r – число
корней характеристического уравнения, равных нулю.
r – число
корней характеристического уравнения, равных нулю.
Пример 1. Найти общее решение уравнения

Общее решение соответствующего однородного уравнения имеет вид

Так как правая часть уравнения –
многочлен первой степени и ни один из корней характеристического уравнения  не равен нулю (
не равен нулю (

где А и В – неизвестные
коэффициенты. Дифференцируя дважды  и подставляя
и подставляя 
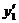 и
и  в данное уравнение,
найдем
в данное уравнение,
найдем

Приравнивая коэффициенты при одинаковых степенях x в обеих частях равенства: A = 1, -2А + В = 1, находим: А = 1, В = 3. Итак, частное решение данного уравнения имеет вид

а его общее решение

II. Правая часть имеет вид
 (2.3.3)
(2.3.3)
где  - многочлен степени n. Тогда частное решение следует искать
в виде
- многочлен степени n. Тогда частное решение следует искать
в виде
 (2.3.4)
(2.3.4)
где  - многочлен той же
степени, что и
- многочлен той же
степени, что и  r – число
корней характеристического уравнения равных
r – число
корней характеристического уравнения равных 


1)
Пусть  не является корнем
характеристического уравнения
не является корнем
характеристического уравнения
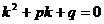
т.е. 
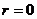



После подстановки функции  и ее производных в
уравнение (2.3.3), сокращения ее на
и ее производных в
уравнение (2.3.3), сокращения ее на 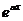
 (2.3.5)
(2.3.5)
Слева – многочлен степени n с неопределенными коэффициентами,
справа – многочлен степени n, но с
известными коэффициентами. Приравнивая коэффициенты при одинаковых степенях x, получим систему (n+1) алгебраических уравнений для определения коэффициентов 
2)
Пусть  является однократным
(простым) корнем характеристического уравнения
является однократным
(простым) корнем характеристического уравнения 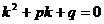

В этом случае искать
решение в форме  нельзя, т.к.
нельзя, т.к. 

В левой части - многочлен степени
(n-1), в правой части – многочлен степени n. Чтобы получить тождество
многочленов в решении  n+1). Поэтому частное решение
n+1). Поэтому частное решение  следует искать в виде
следует искать в виде

(в равенстве (2.3.4) положить r = 1).
3)
Пусть  является двукратным
корнем характеристического уравнения
является двукратным
корнем характеристического уравнения 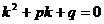

 и
и 

Слева стоит многочлен
степени (n-2). Понятно, чтобы иметь слева многочлен степени n, частное решение  следует искать в виде
следует искать в виде
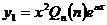
(в равенстве (2.3.4) положить r = 2).
Пример 2. Найти общее решение уравнения

Характеристическое
уравнение  имеет корни
имеет корни 

 В правой части этого
уравнения – произведение многочлена первой степени на показательную функцию
В правой части этого
уравнения – произведение многочлена первой степени на показательную функцию 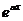 при
при 
 = 1. В
данном случае
= 1. В
данном случае  - многочлен первой
степени. Поэтому частное решение данного уравнения ищем в виде
- многочлен первой
степени. Поэтому частное решение данного уравнения ищем в виде

Дифференцируя и подставляя в уравнение, получаем
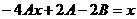
Приравнивая коэффициенты при
одинаковых степенях x в обеих частях
равенства: 


 А и В в выражение для
А и В в выражение для 


III. Правая часть имеет вид

где  и
и  - известные числа.
Тогда частное решение
- известные числа.
Тогда частное решение  надо искать в виде
надо искать в виде

где А и В – неизвестные
коэффициенты, а r – число корней
характеристического уравнения, равных 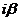
Пример 3. Найти общее решение уравнения

Характеристическое
уравнение 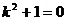 имеет корни
имеет корни 





 - корень
характеристического уравнения, то r =
1 и частное решение надо искать в виде
- корень
характеристического уравнения, то r =
1 и частное решение надо искать в виде

Дифференцируя и подставляя в уравнение, получаем

откуда 
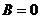


IV. Правая часть имеет вид

где  и
и  - многочлены степени n и m
соответственно,
- многочлены степени n и m
соответственно,  и
и  - действительные числа.
Уравнение (2.3.1) запишется в виде
- действительные числа.
Уравнение (2.3.1) запишется в виде

Тогда частное решение следует искать в виде

где r – число, равное кратности  как корня
характеристического уравнения
как корня
характеристического уравнения 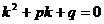
 и
и  - многочлены степени l с неопределенными коэффициентами, l – наивысшая степень многочленов
- многочлены степени l с неопределенными коэффициентами, l – наивысшая степень многочленов  и
и 

Пример 4. Найти общее решение уравнения

Здесь характеристическое
уравнение  имеет корни
имеет корни 




 не является корнем
характеристического уравнения, поэтому r = 0, и
частное решение ищем в виде
не является корнем
характеристического уравнения, поэтому r = 0, и
частное решение ищем в виде

Дифференцируя и подставляя в уравнение, получаем

Приравнивая коэффициенты при  и
и 


откуда 



Глава III
Вынужденные колебания материальной точки
§3.1 Применение линейных уравнений второго порядка с постоянными коэффициентами к исследованию простейших колебаний
Рассмотрим прямолинейное движение материальной точки массы m по оси x. Пусть движение происходит под действием трех сил:
1) силы, притягивающей точку к началу координат и имеющей проекцию на ось x, равную –ax (a>0);
2) силы сопротивления среды, которую будем считать пропорциональной первой степени скорости:

3) возмущающей силы, направленной силы
по оси x и равной  в момент времени t.
в момент времени t.
Тогда, применяя второй закон Ньютона, получим дифференциальное уравнение движения
 (3.1.1)
(3.1.1)
Разделив обе части уравнения (3.1.1) на m, перепишем его в виде
 (3.1.2)
(3.1.2)
где

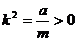

Уравнение (3.1.2) есть неоднородное линейное уравнение второго порядка с постоянными коэффициентами. Проинтегрировав его, найдем закон движения рассматриваемой точки.
Так как наибольший
интерес имеют случаи, когда движения, определяемые равнением (3.1.2),
представляют собой колебания точки около положения x = 0, то уравнение (3.1.2) называют уравнением колебаний. При этом если
возмущающая сила отсутствует, так что 
 (3.1.3)
(3.1.3)
и называется уравнением свободных колебаний. Дифференциальное уравнение (3.1.2),
в котором  вынужденных
колебаний.
вынужденных
колебаний.
К интегрированию линейного уравнения второго порядка с постоянными коэффициентами приходим при изучении не только механических колебаний, но и многих других колебательных явлений: например, с такими уравнениями мы встречаемся в теории электрических цепей.
Уравнение (3.1.2) всегда
интегрируется хотя бы в квадратурах, ибо соответствующее однородное уравнение
(3.1.3), будучи однородным линейным уравнением с постоянными коэффициентами,
всегда интегрируется в элементарных функциях, а тогда, применяя метод Лагранжа,
можно найти общее решение уравнения (3.1.2) при любой непрерывной функции 
 t.
t.
§3.2 Свободные колебания
Рассмотрим
дифференциальное уравнение (3.1.3); изучим свойства решений (движений),
определяемых этим уравнением. В частности, выясним, как влияют параметры h и k
на характер движений. Предположим сначала, что  в среде без сопротивления. В этом случае уравнение (3.1.3)
принимает вид
в среде без сопротивления. В этом случае уравнение (3.1.3)
принимает вид
 (3.2.1)
(3.2.1)
Его характеристическим уравнением будет

откуда 


и общее решение имеет вид
 (3.2.2)
(3.2.2)
Формула (3.2.2) дает все решения (движения), определяемы уравнением (3.2.1).
Введем вместо  и
и  новые произвольные
постоянные А и
новые произвольные
постоянные А и 


Получим движение
 (3.2.3)
(3.2.3)
Такое движение называется
гармоническим колебанием. Как видно
из формулы (3.2.3), оно является периодическим движением с периодом  и частотой k. Число A называется амплитудой,
а
и частотой k. Число A называется амплитудой,
а  - начальной фазой колебания (3.2.3).
- начальной фазой колебания (3.2.3).
|

|
|
|
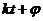 t =
0 называется начальной фазой.)
t =
0 называется начальной фазой.)
|
|
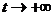
|
|

График движения (3.2.3) (рис. 3.1)
получают в результате элементарных
Рис. 3.1 преобразований графика
функции 
Всякими начальными условиями

 и при
и при 
в силу теоремы существования и
единственности решения задачи Коши для линейного уравнения n-ого порядка
соответствует одно вполне определенное движение; оно содержится в формуле
(3.2.3) при соответствующих значениях амплитуды A и начальной фазы 
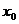 и
и 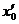 в систему
в систему


Получаем


откуда


В частности, если точка
начинает движение из положения  без начальной скорости
(
без начальной скорости
(


и движение имеет вид
 или
или 
(рис. 3.2).
Если
точка начинает движение из положения  с начальной скоростью
с начальной скоростью 


и соответствующим движением будет (рис. 3.3):

|
|
|
|
|

|
|
|
|
|
|

Рис. 3.2 Рис. 3.3
Наконец, если оба
начальных значения 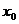 и
и 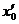 равны нулю, то
равны нулю, то 

т.е. выродится в состояние покоя. Это есть единственное движение, удовлетворяющее нулевым начальным условиям

 при
при  (3.2.4)
(3.2.4)
Скорость этого движения, очевидно, равна нулю при всех t.
Состояние покоя  все
движения, у которых начальные значения
все
движения, у которых начальные значения 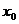 и
и 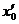 не равны одновременно
нулю, но достаточно малы, будут при всех
не равны одновременно
нулю, но достаточно малы, будут при всех  сколь угодно мало
отклоняется от состояния покоя и иметь сколь угодно малую скорость. Действительно, эти движения имеют вид (общее
решение в форме Коши)
сколь угодно мало
отклоняется от состояния покоя и иметь сколь угодно малую скорость. Действительно, эти движения имеют вид (общее
решение в форме Коши)

Их скорость определяется формулой

Так как синус и косинус по абсолютной величине не превосходят числа 1, то


откуда и следует, что x и  будут сколь угодно
малы при всех
будут сколь угодно
малы при всех 
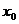 и
и 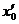 достаточно малы.
достаточно малы.
Предположим
теперь, что в уравнении (3.1.3)  среде с сопротивлением.
среде с сопротивлением.
Выясним, как влияет наличие h на характер колебаний, определяемых уравнением (3.1.3), как изменяется это влияние с изменением величины h (если k постоянно), т.е. какой характер имеет колебание при малых и больших сопротивлениях среды. Для этого найдем общее решение уравнения (3.1.3).
Характеристическое уравнение

имеет корни

Здесь возможны три случая.
Первый случай. 
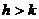
 (3.2.5)
(3.2.5)
Движения, соответствующие
решениям (3.2.5), являются апериодическими.
Выясним, как ведут себя движения (3.2.5) по отношению к состоянию покоя  при
при 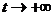
Нетрудно убедиться, что если 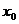 и
и 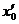 достаточно малы, то
x и
достаточно малы, то
x и  будут сколь угодно
малы при всех
будут сколь угодно
малы при всех  . Кроме того,
все ненулевые решения (3.2.5) обладают свойством:
. Кроме того,
все ненулевые решения (3.2.5) обладают свойством:

 и при
и при 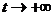 (3.2.6)
(3.2.6)
Второй случай. 


Общим решением уравнения (3.1.3) будет
 (3.2.7)
(3.2.7)
Движения, соответствующие
решениям (3.2.7), также являются апериодическими. Для любых 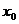 и
и 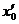 соответствующие им x
и
соответствующие им x
и  будут бесконечно
малыми при
будут бесконечно
малыми при 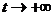 . Другими словами, все ненулевые решения (3.2.7) обладают
свойством (3.2.6).
. Другими словами, все ненулевые решения (3.2.7) обладают
свойством (3.2.6).
Третий случай. 


Поэтому общее решение имеет вид

или
 (3.2.8)
(3.2.8)
Движение, соответствующее
решению (3.2.8), называется затухающими
гармоническим колебанием с периодом  и частотой
и частотой 
 и начальной фазой
и начальной фазой  В отличие от гармонического колебания (3.2.3) здесь
амплитуда уже непостоянна. Заметим, что она ограничена, так как
В отличие от гармонического колебания (3.2.3) здесь
амплитуда уже непостоянна. Заметим, что она ограничена, так как

и стремится к нулю при 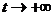 Число А называет начальной амплитудой, а h
– коэффициентом затухания. Множитель
Число А называет начальной амплитудой, а h
– коэффициентом затухания. Множитель  характеризует быстроту
затухания.
характеризует быстроту
затухания.
Начальная амплитуда A и начальная фаза  определяется из
начальных условий. При этом, так как из формулы (3.2.8) следует, что
определяется из
начальных условий. При этом, так как из формулы (3.2.8) следует, что

то графики ненулевых решений (1) (колебаний, отличных от состояния покоя) заключены между графиками показательных функций (2) и (3) (рис. 3.4):
|
 и
и 
|
|
|
|
 Можно показать, что если
Можно показать, что если 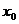 и
и 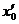 достаточно малы, то
соответствующие им x и
достаточно малы, то
соответствующие им x и  будут сколь угодно
малы при
будут сколь угодно
малы при 
|
|
|
Рис. 3.4 |

|
|
 видоизменяет характер
колебаний;
видоизменяет характер
колебаний;
причем пока сопротивление h сравнительно невелико (
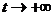 ; при большом сопротивлении среды
; при большом сопротивлении среды  движения становятся
апериодическими.
движения становятся
апериодическими.
Все решения уравнения
(3.1.3) при  обладают свойством
(3.2.6).
обладают свойством
(3.2.6).
§3.3 Вынужденные колебания
Рассмотрим дифференциальное уравнение вынужденных колебаний (3.1.2)

Согласно теореме о структуре общего решения неоднородного линейного уравнения все движения, определяемые уравнением (3.1.2), складываются из совокупности всех движений, определяемых соответствующим однородным уравнением и называемых собственными колебаниями точки, и какого-нибудь однородного движения, определяемого неоднородным уравнением (3.1.2).
Как было отмечено, все колебания, определяемые уравнением (3.1.2), всегда можно найти методом вариации произвольных постоянных.
Если правая часть уравнения (3.1.2) имеет специальный вид, позволяющий найти частное решение методом неопределенных коэффициентов, то метод Лагранжа применять не следует.
Рассмотрим случай, когда
возмущающая сила  периодическая и имеет
синусоидальный характер, причем колебания происходят в среде без сопротивления
(
периодическая и имеет
синусоидальный характер, причем колебания происходят в среде без сопротивления
(
Итак, пусть дано уравнение
 (3.3.1)
(3.3.1)
Здесь собственные колебания, определяемые уравнением (3.2.1)

являются гармоническими колебаниями (3.2.3):

Остается найти частное
решение уравнения (3.3.1). Вид частного решения зависит от того, будет ли число
 корнем характеристического
уравнения (3.2.1), так как это характеристическое уравнение имеет корни
корнем характеристического
уравнения (3.2.1), так как это характеристическое уравнение имеет корни  совпадению
частоты возмущающей силы с частотой собственных колебаний (резонанс) или к несовпадению этих частот (нерезонансный
случай).
совпадению
частоты возмущающей силы с частотой собственных колебаний (резонанс) или к несовпадению этих частот (нерезонансный
случай).
Рассмотрим сначала
нерезонансный случай (
 (3.3.2)
(3.3.2)
где  и
и  - коэффициенты,
подлежащие определению.
- коэффициенты,
подлежащие определению.
Имеем


Поэтому
 (3.3.3)
(3.3.3)
Общим решением уравнения (3.3.1) будет

Вынужденные колебания, определяемые этим общим решением, являются наложениями гармонических колебаний.
§3.4 Явление резонанса
Рассмотрим уравнение вынужденных колебаний
 (3.4.1)
(3.4.1)
Это уравнение есть частный случай
уравнения (3.3.1), когда 

 является простым
корнем характеристического уравнения для соответствующего однородного уравнения
(3.2.1). Поэтому частное решение в отличие от нерезонансного случая,
рассмотренного выше, приобретает множитель t,
т.е. имеет вид
является простым
корнем характеристического уравнения для соответствующего однородного уравнения
(3.2.1). Поэтому частное решение в отличие от нерезонансного случая,
рассмотренного выше, приобретает множитель t,
т.е. имеет вид
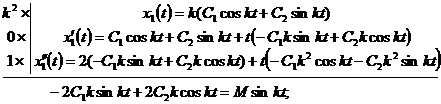

Поэтому
 (3.4.2)
(3.4.2)
Частное решение (3.4.2) представляет
собой вынужденное колебание, оно имеет на  неограниченную
амплитуду. График этого колебания заключен между прямыми (1) и (2) (рис. 3.5):
неограниченную
амплитуду. График этого колебания заключен между прямыми (1) и (2) (рис. 3.5):
 и
и 
|
|
|


|
|
|
|
|
|
Рассмотрим уравнение вынужденных колебаний (3.1.2) в среде с малым сопротивлением
|
Рис. 3.5 |
 (
(
имеет синусоидальный характер
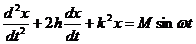 (3.4.3)
(3.4.3)
Собственные колебания имеют вид (3.2.8). Частное решение уравнения (3.4.3) следует искать в виде
 (3.4.4)
(3.4.4)
где коэффициенты  и
и  находятся подстановкой
(3.4.4) в (3.4.3). Получим
находятся подстановкой
(3.4.4) в (3.4.3). Получим
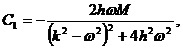
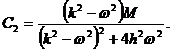
Поэтому
 (3.4.5)
(3.4.5)
Общее решение уравнения (3.4.3) имеет вид

Заметим, что при 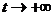 последнее слагаемое
стремиться к нулю, так что при достаточно больших t можно считать, что
последнее слагаемое
стремиться к нулю, так что при достаточно больших t можно считать, что

т.е. собственными (затухающими) колебаниями можно пренебречь.
Амплитуда  вынужденного колебания
(3.4.5) выражается формулой
вынужденного колебания
(3.4.5) выражается формулой

Если сопротивление h очень мало, то 

 k амплитуда
k амплитуда  становится весьма значительной
даже при мало M. Аналогичный вывод,
как нетрудно видеть, можно сделать вблизи резонанса
становится весьма значительной
даже при мало M. Аналогичный вывод,
как нетрудно видеть, можно сделать вблизи резонанса 
Замечание. Однородные линейные дифференциальные уравнения с постоянными коэффициентами, как показано выше, всегда интегрируются в элементарных функциях.
Приведем два примера.
Пример 1. Рассмотрим однородное линейное уравнение Эйлера второго порядка
 (
( (3.4.6)
(3.4.6)
Сделаем замену независимой переменной x на новую независимую переменную t по формуле
 (3.4.7)
(3.4.7)
Нам нужно выразить производные от
искомой функции  по x через производные от
по x через производные от  по t. Имеем
по t. Имеем
 ,
,
так что операторы  и
и  связаны
соотношением
связаны
соотношением
 .
.
Используя это соотношение, находим 

или
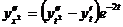
Заменяя теперь в уравнении (3.4.6) x на  , а
, а  и
и  найденными значениями,
получим
найденными значениями,
получим

или

Это уравнение с постоянными коэффициентами. Интегрируя его и возвращаясь к независимой переменной x, найдем общее решение уравнения (3.4.6).
Нетрудно убедиться, что та же подстановка (3.4.7) приводит к уравнению с постоянными коэффициентами и однородное уравнение Эйлера n-ого порядка

Пример 2. Пусть дано уравнение Бесселя
 (
( (3.4.8)
(3.4.8)
Сделаем (однородную линейную) замену
искомой функции y по формуле 
где  - новая неизвестная
функция от x.
- новая неизвестная
функция от x.
Вычисляя  и
и  и подставляя в
уравнение (3.4.8), получим уравнение с постоянными коэффициентами
и подставляя в
уравнение (3.4.8), получим уравнение с постоянными коэффициентами 
Общим решением уравнения Бесселя (3.4.8) будет

Глава IV
Применение явления резонанса
§4.1 Учет и использование резонанса
Жилые дома и промышленные корпуса, железные дороги и самолеты, морские суда и автомобили, космические корабли и ракеты, гидравлические турбины и двигатели внутреннего сгорания, мосты и тоннели являются колебательными системами, в которых при определенных условиях могут возникать вынужденные колебания. Иногда амплитуда вынужденных колебаний становится столь большой, что сооружение может разрушиться. Это заставляет учитывать возможность резонанса в сооружениях. В ряде случаев явление резонанса может быть использовано и для достижения положительного эффекта.
Явление резонанса находит широкое применение в технике. Так, для уплотнения сыпучего основания под фундаменты и дороги, а также для уплотнения бетона используют специальные вибраторы-уплотнители. Существует большое число конструкций вибраторов, но основная часть каждого из них – прочное основание, на котором установлен двигатель с неуравновешенным маховиком или системой неуравновешенных грузов. При работе двигателя насаженные на его ось грузы (или маховик) вызывают колебания всей установки. Для получения больших амплитуд собственную частоту колебаний уплотнителя делают равной частоте вибрации вала двигателя. Колебания виброуплотнителя передаются через площадку грунту или бетону.
Вибраторы, аналогичные описанному, применяются для вибрационного погружения свай, шпунов, труб и т.п. Для вибрационного погружения сваи мощный вибратор устанавливают на ее верхнем основании. При включении двигателя свая начинает вибрировать; грунт под сваей «разжижается», и под действием силы тяжести она погружается. Особенно широкое применение этот метод погружения свай и труб нашел на строительстве морских и озерных сооружений.
Явление резонанса используют для измерения частоты колебаний. Располагая набором резонаторов (колебательных систем с малым затуханием), частоты которых заранее известны, можно определить частоту происходящих колебаний. Частота эта равна частоте наиболее сильно колеблющегося резонатора.
Этот принцип используют, например, в язычковом частотомере, который представляет комплект упругих пластин, имеющих разную частоту свободных колебаний.
Каждая такая пластина, будучи закреплена одним концом в массивной обойме, является колебательной системой, собственная частота которой определяется массой и упругостью пластины.
При колебании пластины ее торцовая часть видна в виде размытой полоски. Измеряемая частота совпадает с частотой колебаний той из пластин, амплитуда колебаний которой наибольшая.
Явление электрического резонанса играет полезную роль при настройке радиоприемника на нужную радиостанцию изменяя величины индуктивности и ёмкости, можно добиться того, что собственная частота колебательного контура совпадёт с частотой электромагнитных волн, излучаемых какой-либо радиостанцией. В результате этого в контуре возникнут резонансные колебания данной частоты, амплитуды же колебаний, создаваемых другими станциями, будут малы. Это приводит к настройке радиоприёмника на нужную станцию.
Явление резонанса давно было известно физикам в области акустики. Оно состоит в следующем. Представьте себе натянутую струну. Она способна, если по ней ударить или провести по ней смычком, звучать в некотором определенном тоне, при этом она приходит в колебания со вполне определенной частотой. Каждому тону соответствует своя частота. Скажем, что наша струна способна совершать 435 колебаний в секунду. Это соответствовало бы тону "ля". Предположим, что струна находится в покое. Возьмем теперь вблизи другую струну, которая тоже способна совершать 435 колебаний в секунду, и заставим эту струну звучать. Тогда окажется, что под влиянием колебаний нашей второй струны приходит в колебания - и сильные колебания - и первая. Это явление называется резонансом. Но если вторая струна имеет отличное от первой число колебаний, то первая струна молчит и на колебания второй струны не отвечает.
Объяснение явления резонанса несложно. Та струна, которую мы заставляем непосредственно колебаться, передает первой струне через воздух маленькие толчки, следующие друг за другом в темпе ее колебаний, т. е. каждую 1/435 сек один толчок. Каждый толчок сам по себе крайне незначителен. Первый толчок действительно приведет струну в ничтожно слабое колебание, но если темп этих колебаний и приходящих толчков один и тот же, то второй толчок придется как раз вовремя и усилит действие первого. Третий усилит колебания еще больше, и т. д. Произойдет накопление действия отдельных толчков, и в результате получается сильное звучание. Между тем если отдельные толчки следуют друг за другом невпопад, то действие одного будет уничтожаться действием следующего и заметного эффекта не будет.
Явление резонанса, изученное впервые в акустике, ею абсолютно не ограничивается. Звонарь на колокольне, раскачивающий тяжелый колокол, пользуется, хотя и бессознательно, тем же явлением. Он не в состоянии преодолеть тяжесть колокола одним усилием и поэтому он поступает так. Он дает веревке слабый толчок: колокол отклоняется, но очень незначительно, а затем возвращается обратно; как раз в момент возвращения звонарь дает следующий толчок и такими ритмичными, следующими в tempo колебаний колокола толчками он его раскачивает до тех пор, пока язык не ударит по колоколу. Вот почему, между прочим, звонить в тяжелый колокол, особенно снизу, при помощи веревки, т. е. в условиях, когда следить за колебанием нельзя, требует немалого навыка.
§4.2 Явление резонанса, ведущее к разрушению. Способы гашения нежелательных вынужденных колебаний
Электрические двигатели, паровые и газовые турбины, двигатели внутреннего сгорания даже из-за небольшой несбалансированности вращающихся масс являются источником колебаний, передающихся основаниям, на которых они установлены. Если двигатель жестко укреплен на фундаменте, колебания почти полностью передаются грунту и через грунт зданию, в котором машина установлена.
Если колебательная система обладает малым трением, то лишь небольшая часть подводимой к ней энергии превращается во внутреннюю энергию системы. В этих условиях (при совпадении частоты вынуждающих колебаний с частотой свободных колебаний) амплитуда вынужденных колебаний может достичь больших значений и вызвать разрушение здания.
Во второй половине прошлого столетия стали обращать на себя внимание инженеров случаи непонятных обрушений мостов, особенно цепных мостов, которые в то время как раз строились в сравнительно большом количестве. Непонятных - потому, что мосты рушились под весьма небольшой тяжестью, которую они по расчету должны были свободно выдерживать и фактически раньше выдерживали. Повторные проверки не обнаруживали ошибочности расчетов, а катастрофы были налицо. Инженеры беспомощно стояли перед совершившимися несчастиями и не имели средств предотвратить их в будущем.
И только в последнем десятилетии прошлого века решение вопроса было найдено. Вот что оказалось. Цепной мост представляет собой не жесткую систему, а систему, которая может, подобно струне, совершать колебания, с той разницей, что струна колеблется быстро, совершая несколько сот колебаний в секунду, в то время как мост, если его заставить колебаться, совершает за секунду, скажем, одно или даже меньше колебаний. И вот при известных условиях нагрузки наступало так называемое явление резонанса, несшее гибель мосту.
Известно много случаев, когда источником опасных колебаний механических сооружений были люди, идущие в ногу. Например, в 1831 году в Манчестере по мосту через реку Ирвель проходили строем, шагая в ногу, 60 солдат. Частота ударов солдатских ног совпала с частотой свободных колебаний моста, и мост разрушился. Аналогичный случай произошел в 1905 году в Петербурге, когда был разрушен цепной мост через реку Фонтанку в результате прохождения по нему эскадрона гвардейской кавалерии. Частота ударов ног хорошо обученных лошадей совпала с частотой свободных колебаний моста. Цепи, на которых висел мост, разорвались, мост обрушился.
Теперь ясно, как явление резонанса может оказаться губительным для моста. Представьте себе, и это действительно бывало при некоторых катастрофах, что по мосту проходит военный отряд, идущий в ногу. Отдельные толчки, производимые при этом, не оказывают сколько-нибудь заметного действия. Но если случайно период этих ритмических толчков совпадает с периодом колебаний моста - а это, особенно в цепных мостах, может случаться очень легко, - то наступает явление резонанса. Действия отдельных толчков накапливаются, мост раскачивается все сильнее, материал не выдерживает, и мост рушится. Вот почему, между прочим, теперь при проходе отряда через такой мост солдатам дается команда идти не в ногу. Это, конечно, одна из причин, а подобных причин наступления резонанса может быть множество, и оградить себя от таких ритмических нагрузок трудно. Поэтому в настоящее время - а это и есть главный практический результат, к которому привела теория, - почти совершенно отказались от нежестких систем, имеющих собственные колебания.
Современные конструкции имеют гораздо большую жесткость, чем прежние цепные мосты, и этим возможность колебаний, а значит и возможность наступления губительного резонанса, устраняется.
Теперь также стало ясным, почему случаи, подобные описанному, казались непонятными и загадочными. Конструкторы рассчитывали прочность своих мостов исключительно статически, т. е. они принимали во внимание только постоянную нагрузку, и с этой точки зрения их расчеты были совершенно правильны. Они не учитывали и даже не напали на мысль о необходимости учета ритмически изменяющейся нагрузки, с одной стороны, и колебаний моста - с другой. Их кругозор был ограничен и не охватывал явлений во всем их разнообразии. Но нашлись люди с широкой теоретической подготовкой, для которых звучание струны и колебания моста являлись лишь частными случаями, охватываемыми одним общим законом, и вопрос был решен.
Интересно, что аналогичное явление повторилось в совершенно другой области. Вы знаете, что для передачи электрической энергии пользуются иногда кабелем, состоящим по существу из двух металлических проводников, несущих ток, и изолированных друг от друга каким-нибудь изолирующим веществом, например гуттаперчей. Слой гуттаперчи между проводами должен быть больше или меньше, смотря по тому электрическому напряжению, иначе говоря, смотря по числу вольт, при котором передача энергии идет. Понятно при этом, что из соображений экономии и из-за тяжести кабеля слой гуттаперчи делают не больше (конечно, с известным запасом), чем это нужно для данного случая. Проверка делается в заводской лаборатории. Для этого соединяют один провод с положительным, другой - с отрицательным полюсом батареи и смотрят, выдерживает ли кабель нужное напряжение. И вот наблюдались случаи, что при работе с переменным током кабель, полностью выдержавший испытание в лаборатории, в работе пробивался.
Вопрос разъяснился и здесь тоже лишь тогда, когда к нему подошли с физико-теоретической стороны. Оказалось, что здесь, как и в случае моста, губительным фактором было явление резонанса. Дело в том, что кабель, смотря по длине, имеет различные периоды собственных электрических колебаний. Он представляет собой электрическую аналогию струны. С другой стороны, отличительной чертой переменного тока является его ритмическая пульсация.
И вот, если длина кабеля оказывалась такова, что период пульсации тока совпадал с периодом колебаний кабеля, наступало явление резонанса, происходило нарастание колебаний электрического напряжения, которое благодаря этому достигало гораздо большей величины, чем то, которое давали динамо-машины и на которое был рассчитан кабель, и изоляция пробивалась.
С резонансом можно встретиться не только на суше, но и в море и даже в воздухе. Так, например, при некоторых частотах вращения гребного вала в резонанс входили целые корабли. А на заре развития авиации некоторые авиационные двигатели вызывали столь сильные резонансные колебания частей самолета, что он разваливался в воздухе.
То обстоятельство, что амплитуда вынужденных колебаний может достичь опасных для конструкций значений, заставило искать способы гашения вынужденных колебаний.
Один способ гашения вынужденных
колебаний состоит в измерении частоты свободных колебаний системы, так чтобы
она не совпала с частотой вынуждающих колебаний и не была ей кратна. Например,
при изготовлении паровой турбины для теплоэлектростанции учитывают, что турбина
будет работать при частоте 3000 мин-1. Следовательно, колебания,
вызываемые вращением ротора, будут иметь частоту  Чтобы избежать
резонансных колебаний, вся система «генератор – турбина – фундамент» должна
иметь частоту свободных колебаний, отличную от 50 и не кратную 50.
Чтобы избежать
резонансных колебаний, вся система «генератор – турбина – фундамент» должна
иметь частоту свободных колебаний, отличную от 50 и не кратную 50.
Проиллюстрируем этот способ борьбы с опасными последствиями на опыте. Соберем установку, показанную на рисунке 4.1. При включении вибратора пружинный маятник начинает колебаться с все возрастающей амплитудой, что свидетельствует о том, что частота вынужденных колебаний близка к частоте свободных колебаний.
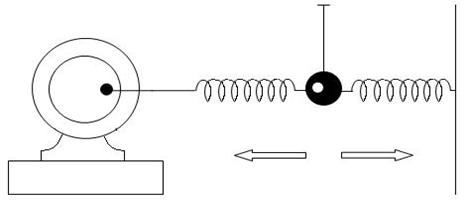
Рис. 4.1
Остановив маятник, заменим его груз другим грузом большей массы (этим мы изменим собственную частоту колебаний маятника). Вновь включив вибратор, увидим, что амплитуда колебаний маятника стала значительно меньше. Теперь колебания не имеют резонансного характера.
Другой способ борьбы заключается в увеличении трения системы (рис. 4.2): чем больше трение, тем меньше амплитуда резонансных колебаний.

Рис. 4.2
§4.3 Дифференциальное уравнение цепной линии

Для данного пролета s и ширины моста b вес проездного пути  v принимаются за известные. Например,
для тяжелых городских уличных мостов и мостовой на них можно принять
v принимаются за известные. Например,
для тяжелых городских уличных мостов и мостовой на них можно принять 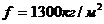 для проездного пути и
для проездного пути и  для нагрузки движения.
Оба рода нагрузки принимаются равномерно распределенными по пролету s. Если положить число висячих цепей
по одной стороне моста равным N, то через каждую из них на любой из
проволочных канатов передается нагрузка
для нагрузки движения.
Оба рода нагрузки принимаются равномерно распределенными по пролету s. Если положить число висячих цепей
по одной стороне моста равным N, то через каждую из них на любой из
проволочных канатов передается нагрузка 


Рис. 4.3
Для подготовки решения исследуем некоторое число заданных параллельных сил на плоскости (рис.4.4):


 и попытаемся найти между ними такое
расположение каната, при котором эти силы будут находиться в равновесии.
и попытаемся найти между ними такое
расположение каната, при котором эти силы будут находиться в равновесии.

Рис. 4.4 Рис. 4.5
Отложим силы по величине (1 мм = 100 кг) и по направлению на прямой, параллельной направлению сил (рис.4.5), вследствие чего на ней получаются точки 0, 1, …, 7.
Из произвольного выбранного полюса О, проводим прямые линии в точки 0 – 7, благодаря чему получается диаграмма усилий 0-7-0.
К прямым от 0-0 до 0-7 проводят 8
параллелей (рис.4.4) так, чтобы две последующих пересекались на одной из линий,
по которым расположены силы 
 0-1-2-3-4-5-6-7.
0-1-2-3-4-5-6-7.
Рассмотрим теперь стороны веревочного многоугольника, как состоящие из действительных кусков каната, из которых первый (0) и последний (7) прикреплены к двум неподвижным точкам А и В (рис.4.4).
В узловых точках вообразим
приложенными параллельные силы 

Натяжения отдельных частей троса
могут быть определены из-за диаграммы усилий; они равны прямым линям 0-0 и 0-7,
если будут в том же масштабе, как и силы 
Напряжение 0,0 = 4500 кг 0,4 = 3200 кг
0,1 = 3800 кг 0,5 = 3400 кг
0,2 = 3450 кг 0,6 = 3900 кг
0,3 = 3200 кг 0,7 = 4450 кг
Для точки многоугольника 5 нарисован
параллелограмм сил 

 = 05 (рис.4.6 и 4.7).
= 05 (рис.4.6 и 4.7).


Рис. 4.6 Рис. 4.7
Все напряжения троса обладают тем свойством, что при разложении на вертикальное и горизонтальное направления последнее в точности равно горизонтальной составляющей H, которая в предыдущем случае составляет 3150 кг. Величину H называют горизонтальным натяжением веревочного многоугольника.
Этот факт получается прямо из рис. 4.5 разложением напряжения троса 0-0 до 0-7 на вертикальную и горизонтальную составляющую Н.
Величина АВ называется пролетом веревочного многоугольника. Веревочный многоугольник вполне определен, ели даны: система сил, опоры А и В и горизонтальное натяжение.
Чем больше принята при заданной системе сила горизонтального натяжения, тем более плоским становится веревочный многоугольник и тем больше становятся натяжениях отдельных частях троса. Горизонтальное натяжение определяется расстоянием полюса О до линии сил 0-7 (рис.4.8).
При этом выбор полюса произволен и влияет на положение опорных пунктов. Поэтому выбор полюса следует делать так, чтобы положение опорных пунктов, которым он соответствует, совпало с данным. Например, если хотят, чтобы опорные точки А и В имели расположение, указанное на рис.5, тогда нужно только вертикальные растяжения углов по прямой АВ, взятые на рис.4.9. После этого получится фигура равновесия каната.
II. Возвратимся теперь к висячему мосту (рис.4.3). Вся его длина пусть равна
40 м, ширина 20 м, N = 20 подвесных канатов. Таким
образом на каждый из них приходится нагрузка 

Рис. 4.8
Эти 20 нагрузок Р отложим на диаграмме усилий друг за другом – это отрезки между точками 0,1,2,…,20. После выбора полюса, для горизонтального натяжения Н, о котором мы будем говорить потом, получится веревочный многоугольник 0123…20. Последний тотчас дает форму каната висячего моста, если полюс О поместить симметрично – на перпендикуляре линии 0123…20 рис. 4.9. На этом рисунке видно, что в данном случае, в иду большого числа рассматриваемых сил Р, многоугольник похож на кривую. Это сходство еще более возрастает при увеличении числа вертикальных канатов моста.

Рис. 4.9
III. Таким образом можно прейти в пределе к равномерному распределению
нагрузки на опорный канат моста. При этом можно оставить случай постоянной по
величине нагрузки и считать, что имеется какая-то неравномерная нагрузка  x – расстояния от опоры А. на рис. 4.10 график это нагрузки
представлен кривой DE. В этом случае тоже можно нарисовать многоугольник сил, причем вся
нагрузка Q выразиться интегралом
x – расстояния от опоры А. на рис. 4.10 график это нагрузки
представлен кривой DE. В этом случае тоже можно нарисовать многоугольник сил, причем вся
нагрузка Q выразиться интегралом

Ее откладывают по вертикали ON. Напряжение в какой-нибудь точке Р висячей цепи получают, если провести в Р касательную и через полюс параллель с ней до пересечения с вертикалью ON. Расстояние полюса от вертикали ON равно натяжению в наинизшей точке висячего каната. Во всех точках каната горизонтальная составляющая натяжения остается постоянной.
Чтобы найти форму висячего каната вычислительным путем, введем систему координат xy с началом в точке А. Направление положительных y возьмем вниз, абсциссы будем считать направо.
Рассмотрим бесконечно малый элемент
кривой, на которой расположится канат. Вообразим этот элемент вырезанным из
каната. Чтобы равновесие его сохранялось, к нему должны быть приложены слева и
справа силы натяжения каната S и S1. Кроме них на элемент действует еще
вертикальная сила нагрузки  S и S1 на горизонтальные и вертикальные
составляющие.
S и S1 на горизонтальные и вертикальные
составляющие.
По условию равновесия горизонтальные составляющие слева и справа равны:
H = H1.
Это совпадет с известным раньше обстоятельством – горизонтальная составляющая величина постоянная.



Рис. 4.10
Условие для вертикальных составляющих дает:
 (4.3.1)
(4.3.1)
Так как можно написать, что 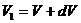
 (4.3.2)
(4.3.2)
Принимая во внимание, что напряжение направлено по касательной, имеем:
 (4.3.3)
(4.3.3)
отсюда
 (4.3.4)
(4.3.4)
Величина Н постоянная. Поэтому дифференцирование дает:
 (4.3.5)
(4.3.5)
Подставляет это
в (4.3.2) и сокращая 
 (4.3.6)
(4.3.6)
Это и есть дифференциальное уравнение цепной линии, по которой располагается канат, на каждый элемент которого действует нагрузка q.
Оно второго
порядка, так как в нем имеется вторая производная неизвестной функции 
Полагая
 (4.3.7)
(4.3.7)
можем сразу интегрировать уравнение
 (4.3.8)
(4.3.8)
После интегрирования получаем:
 (4.3.9)
(4.3.9)
Интегрируя еще раз, находим:
 (4.3.10)
(4.3.10)
или проще:
 (4.3.11)
(4.3.11)
Здесь С1 и С2 – две произвольные постоянные, получающиеся при интегрировании. Всякая определенная пара их значений дает частный интеграл. Таким образом существует, как и следует ожидать, бесчисленное множество цепных линий. Из этого множества надо выбрать нужную, которая выполняет прочные условия, подразумевающиеся в задаче. Таким условием может явиться требование, чтобы кривая проходила через две данные точки.
Вопрос об этих
условий мы разберем для простейшего случая, когда нагрузка равномерно
распределена по длине пролета l. Тогда 
 (4.3.12)
(4.3.12)
так как y – квадратичная функция от x, то форма кривой – парабола. Дополнительных условий два: 1) кривая должна проходить через точку x = 0, y = 0, т.е. через левую опору, и 2) правая опора должна быть ниже, чем левая на a единиц, т.е. кривая должная проходить через точку x = l, y = a. Из первого условия находим:
 (4.3.13)
(4.3.13)
а из второго получится:
 (4.3.14)
(4.3.14)
отсюда
 (4.3.15)
(4.3.15)
Подставляя значения С1 и С2 в (4.3.12), находим тот частный интеграл, который нужен для данной задачи:
 (4.3.16)
(4.3.16)
Здесь участвует еще величина горизонтальной составляющей натяжения, т.е. H. Ее величина не изменится, если изменить а. Полагая в (4.3.16) а = 0, получим:
 (4.3.17)
(4.3.17)
Провес каната f при этом
получается из (4.3.17) при 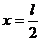
 (4.3.18)
(4.3.18)
Отсюда при данном f можно найти Н.
Заключение
Вынужденные колебания и резонанс широко используются в технике, особенно в акустике, электротехнике, радиотехнике и других областях. Явление резонанса используется в тех случаях, когда из большого набора колебаний разной частоты хотят выделить колебания вполне определенной частоты. Резонанс используется и при измерении очень слабых периодически повторяющихся величин.
Однако в ряде случаев резонанс - нежелательное явление, так как может привести к большим деформациям и разрушению конструкций. Резонанс приходится учитывать при конструировании машин и различных сооружений.
Вращающиеся части машин, валы двигателей самолетов и кораблей невозможно абсолютно точно уравновесить. В результате они испытывают переменную нагрузку, совершая вынужденные колебания и вызывая вынужденные колебания всей системы (например, самолета). Различные части системы или система в целом могут прийти в резонанс с вынуждающей силой, что может привести к их разрушению или повреждению. Поэтому инженеры должны так конструировать ту или иную установку, чтобы не возникало резких резонансных явлений ни во всей установке, ни в ее отдельных частях.
Список литературы
1) . Александров Н.В. и Яшкин А.Я. Курс общей физики. Механика. М.: “Просвещение”, 1978 г.
2) Айнс Э.Л. Обыкновенные дифференциальные уравнения (перевод с английского) под ред. Эфрос А.М.. ОНТИ. Харьков, 1939 г. – 719 с.
3) Арнольд В.И. Геометрические методы в теории обыкновенных дифференциальных уравнений. – Ижевск: Ижевская республиканская типография, 2000 г., 400 с.
4) Арнольд В.И., Ильяшенко Ю.С. Обыкновенные дифференциальные уравнения. М.: Наука, 1972 г., 149 с.
5) Бибиков Ю.Н. Курс обыкновенных дифференциальных уравнений. М.: Высшая школа, 1991 г., 303 с.
6) Гершензон Е.М., Малов Н.Н. Курс общей физики: Механика. -М., “Просвещение”, 1987 г.
7) Голубев В.В. Лекции по аналитической теории дифференциальных уравнений. М.: Гос. изд. технико-теоретической литературы 1950 г., 436 с.
8) Зельдович Я.Б., Мышкис А.Д. Элементы прикладной математики. М.: Наука 1965 г., 616 стр. с илл.
9) Зельдович Я.Б. Высшая математика для начинающих физиков и техников. М.: Наука, 1972 г., 510 с.
10) Коддингтон Э.А., Левинсон Н. Теория обыкновенных дифференциальных уравнений (перев. с английского Левитана Б.М.). М.: Изд. иностранной литературы, 1958 г., 475 с.
11) Курант Р. Курс интегрального и дифференциального исчисления. М., 1970 г., 672 стр. с илл.
12) Лефшец С. Геометрическая теория дифференциальных уравнений. М.: Изд. иностр. лит., 1960 г., 388 с.
13) Матвеев Н.М. Обыкновенные дифференциальные уравнения: Учеб. Пособие для студентов пед. ин-тов и физ.-мат. спец. СПб.: Спец. Литература, 1996.
14) Матвеев Н.М. Сборник задачи упражнений по обыкновенным дифференциальным уравнениям: Учебное пособие, 7-е изд., доп. – Спб.: Издательство «Лань», 2002. – 432 с. – (Учебники для вузов. Специальная литература).
15) Мышкис А.Д. Лекции по высшей математике. М.: Изд. «Наука», 1973 г., 640 с. с илл.
16) Понтрягин Л.С. Обыкновенные дифференциальные уравнения, гос. изд. физ.-мат. литературы, М., 1961 г.
17) Преподавание физики в высшей школе. Сборник научных трудов. №1. -М., изд. МПГТУ. 1994 г.
18) Хайкин С.Э. Физические основы механики. - М.,физматгиз,1963.
19)

