Оценивание параметров и проверка гипотез о нормальном распределении (WinWord, Excel)
| Загрузить архив: | |
| Файл: 025-0014.zip (75kb [zip], Скачиваний: 102) скачать |
|
|

Кафедра математической статистики и эконометрики
Расчетная работа №1
По курсу:
“Математическая статистика”
по теме:
“Оценивание параметров
и проверка гипотез
о нормальном распределении”
Группа: ДИ 202
Студент: Шеломанов Р.Б.
Руководитель: Кацман В.Е.
Москва 1999
Содержание
TOC "заглавн;1" ЗАДАНИЕ № 23--------------------------------------------------------------------------------- PAGEREF _Toc445447422 h 3
Построение интервального вариационного ряда распределения PAGEREF _Toc445447423 h 3
Вычисление выборочных характеристик распределения PAGEREF _Toc445447424 h 4
Графическое изображение вариационных рядов--------- PAGEREF _Toc445447425 h 5
Расчет теоретической нормальной кривой распределения PAGEREF _Toc445447426 h 6
Проверка гипотез о нормальном законе распределения PAGEREF _Toc445447427 h 7
ЗАДАНИЕ № 23
Продолжительность горения электролампочек(ч) следующая:
|
750 |
750 |
756 |
769 |
757 |
767 |
760 |
743 |
745 |
759 |
|
750 |
750 |
739 |
751 |
746 |
758 |
750 |
758 |
753 |
747 |
|
751 |
762 |
748 |
750 |
752 |
763 |
739 |
744 |
764 |
755 |
|
751 |
750 |
733 |
752 |
750 |
763 |
749 |
754 |
745 |
747 |
|
762 |
751 |
738 |
766 |
757 |
769 |
739 |
746 |
750 |
753 |
|
738 |
735 |
760 |
738 |
747 |
752 |
747 |
750 |
746 |
748 |
|
742 |
742 |
758 |
751 |
752 |
762 |
740 |
753 |
758 |
754 |
|
737 |
743 |
748 |
747 |
754 |
754 |
750 |
753 |
754 |
760 |
|
740 |
756 |
741 |
752 |
747 |
749 |
745 |
757 |
755 |
764 |
|
756 |
764 |
751 |
759 |
754 |
745 |
752 |
755 |
765 |
762 |
По выборочным данным, представленным в заданиях №1-30, требуется:
1* Построить интервальный вариационный ряд распределения;
Построение интервального вариационногорядараспределения
Max: 769
Min:733
R=769-733=36
H= R / 1+3,32 lg n=36/(1+3,32lg100)=4,712
A1= x min - h/2=730,644
B1=A1+h; B2=A2+h

2* Вычислить выборочные характеристики по вариационному ряду:
среднюю арифметическую (x ср.), центральные моменты (мю к, к=1,4), дисперсию (S^2), среднее квадратическое отклонение (S), коэффициенты асимметрии (Ас) и эксцесса (Ек), медиану (Ме), моду (Мо), коэффициент вариации(Vs);
Вычисление выборочных характеристик распределения
Di=(xi- xср)
 xср =å xi mi/å mi
xср =å xi mi/å mi
xср=751,7539
Вспомогательная таблица ко второму пункту расчетов

Выборочный центральный момент К-го порядка равен






 M k = ( xi - x)^k mi/ mi
M k = ( xi - x)^k mi/ mi



В нашем примере:
|
Центр момент 1 |
0,00 |
|
Центр момент 2 |
63,94 |
|
Центр момент 3 |
-2,85 |
|
Центр момент 4 |
12123,03 |
Выборочная дисперсия S^2 равна центральному моменту второго порядка:
В нашем примере:
S^2=63,94
Ввыборочное среднее квадратическое отклонение:
В нашем примере:
S=7,996
Выборочные коэффициенты асимметрии Ас и эксцесса Fk по формулам
Ac = m3/ S^3;
В нашем примере:
Ас =-0,00557
Ek = m4/ S^4 -3;
В нашем примере:
Ek = -0,03442
Медиана Ме - значение признакаx (e), приходящееся на середину ранжированного ряда наблюдений( n = 2l -1). При четном числе наблюдений( n= 2l)медианой Ме является средняя арифметическая двух значений, расположенных в середине ранжированного ряда: Me=( x(e) + x( e+1) /2
Если исходить из интервального ряда, то медиану следует вычислять по ормуле
Me= a me +h * ( n/2 - mh( me-1) / m me
где mе- означает номер медианного интервала, ( mе -1) - интервала, редшествующего медианому.
В нашем примере:
Me=751,646
Мода Мо для совокупности наблюдений равна тому значению признака ,которому соответствует наибольшая частота.
Для одномодального интервального ряда вычисление моды можно производить по формуле
Mo= a mo + h * ( m mo- m(mo-1))/2 m mo- m( mo-1) - m( mo+1)
где мо означает номер модального интервала ( интервала с наибольшей частотой), мо-1, мо+1- номера предшествующего модальному и следующего за ним интервалов.
В нашем примере:
Mo = 751,49476
Так какХср, MoMe почти не отличаются друг от друга, есть основания предполагать теоретическое распределение нормальным.
 Коэффициент вариации Vs
= S/ x * 100 %= 3.06%
Коэффициент вариации Vs
= S/ x * 100 %= 3.06%
В нашем примере:
Vs= 1,06%
3* Построить гистограмму, полигон и кумуляту.
Графическое изображение вариационных рядов
Для визуального подбора теоретического распределения, а также выявления положения среднего значения (x ср.) и характера рассеивания (S^2 и S) вариационные ряды изображают графически.
Полигон и кумулята применяются для изображения как дискретных, так и интервальных рядов, гистограмма – для изображения только интервальных рядов. Для построения этих графиков запишем вариационные ряды распределения (интервальный и дискретный) относительных частот (частостей)
Wi=mi/n, накопленных относительных частот Whi и найдем отношение Wi/h, заполнив таблицу 1.4.
Интервалы xi WiWhi Wi/h
Ai-bi
1 2 3 4 5
4,97-5,08 5,03 0,02 0.02 0,18
5,08-5,19 5,14 0,03 0,05 0,27
5,19-5,30 5,25 0.12 0,17 1,09
5,30-5,41 5,36 0,19 0,36 1,73
5,41-5,52 5,47 0,29 0,65 2,64
5,52-5,63 5,58 0,18 0,83 1,64
5,63-5,74 5,69 0,13 0,96 1,18
5,74-5,85 5,80 0,04 1,00 0,36
|
-1,00 - |
Для построения гистограммы относительных частот (частостей) на оси абсцисс откладываем частичные интервалы, на каждом из которых строим прямоугольник, площадь которого равна относительной частотеWiданного i-го интервала. Тогда высота элементарного прямоугольника должна быть равна Wi/h,. Следовательно, позади под гистограммой равна сумме всех носительных частот, т.е. единице.
Из гистограммы можно получить полигон того же распределения. Если середины верхних оснований прямоугольников соединить отрезками прямой.
4* Сделать вывод о форме ряда распределения по виду гистограммы и полигона, а также по значениям коэффициентов Ас и Ек.
4 Анализ графиков и выводы
Гистограмма и полигон являются аппроксимациями кривой плотности (дифференциальной функции) теоретического распределения (генеральной совокупности). Поэтому по их виду можно судить о гипотическом законе распределения.
Для построения кумуляты дискретного ряда по оси абсцисс откладывают значения признакаxi, а по оси ординат – накопленные относительные частоты Whi. Для интервального ряда по оси абсцисс откладывают интервалы .
С кумулятой сопоставляется график интегральной функции распределения F(x).
В нашем примере коэффициенты асимметрии и эксцесса не намного отличаются от нуля. Коэффициент асимметрии оказался отрицательным (Ас=-0,005), что свидетельствует о небольшой левосторонней асимметрии данного распределения. Эксцесс оказался также отрицательным (Ек= -0,034). Это говорит о том, что кривая, изображающая ряд распределения, по сравнению с нормальной, имеет несколько более плоскую вершину. Гистограмма и полигон напоминают кривую нормального распределения (рис.1.1 и 1.2.). Все это дает возможность выдвинуть гипотезу о том, что распределение продолжительности горения электролампочек является нормальным.
Приечание: Кумулята, гистронрамма и полигон находятся в приложениях к работе.
5* Рассчитать плотность и интегральную функцию теоретического нормального распределения и построить эти кривые на графиках гистограммы и кумуляты соответственно.
Расчет теоретической нормальной кривой распределения
Приведем один из способов расчета теоретического нормального распределения по двум найденным выборочным характеристикам x и S эмпирического ряда.
При расчете теоретических частот m^тi за оценку математического ожидания(мю) и среднего квадратического отклонения Gнормального закона распределения принимают значения соответствующих выборочных характеристик x ср. и S, т.е. (мю)=Xср.= 751,7539; G=S=7,99.
Теоретические частоты находят по формуле: M^i=npi,
гдеn – объем; Pi – величина попадания значения нормально распределенной случайной величины в i-й интервал.
Вероятность Pi определяется по формуле
Pi=P(ai
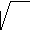
Где Ф(t)=2 2(пи)=интегралу с границами от (0;t) е^x2/2dx - интегральная функция Лапласа – находится по таблице для
T2i=bi-x ср. S
T1i=ai-x ср.S
Таблицы Для вычисления вероятности нормальной кривой распределения
|
Интервалы |
Mi |
T1 |
T2 |
1/2Ф(T1) |
1/2Ф(T2) |
Pi |
|||
|
a(i) |
b(i) |
||||||||
|
730,644 |
735,356 |
2 |
-2,640 |
-2,051 |
0,4958 |
0,4798 |
-0,0080 |
||
|
735,356 |
740,068 |
8 |
-2,051 |
-1,461 |
0,4798 |
0,4279 |
-0,0260 |
||
|
740,068 |
744,780 |
6 |
-1,461 |
-0,872 |
0,4279 |
0,3078 |
-0,0601 |
||
|
744,780 |
749,492 |
18 |
-0,872 |
-0,283 |
0,3078 |
1,1103 |
0,4013 |
||
|
749,492 |
754,204 |
35 |
-0,283 |
0,306 |
0,0300 |
0,6619 |
0,3160 |
||
|
754,204 |
758,916 |
12 |
0,306 |
0,896 |
0,1179 |
0,3133 |
0,0977 |
||
|
758,916 |
763,628 |
11 |
0,896 |
1,485 |
0,3133 |
0,4306 |
0,0587 |
||
|
763,628 |
768,340 |
6 |
1,485 |
2,074 |
0,4306 |
0,4808 |
0,0251 |
||
|
768,340 |
773,052 |
2 |
2,074 |
2,664 |
0,4808 |
0,4960 |
0,0076 |
||
|
Pi*n |
Mi(теор) |
Mi(теор)/h |
Mi(теор)накоп |
||||||
|
-0,8000 |
1 |
0,002 |
0,0080 |
||||||
|
-2,5950 |
3 |
0,006 |
0,0340 |
||||||
|
-6,0050 |
6 |
0,013 |
0,0940 |
||||||
|
40,1250 |
40 |
0,085 |
0,4953 |
||||||
|
31,5950 |
32 |
0,068 |
0,8153 |
||||||
|
9,7700 |
10 |
0,021 |
0,9130 |
||||||
|
5,8650 |
6 |
0,012 |
0,9716 |
||||||
|
2,5100 |
3 |
0,005 |
0,9967 |
||||||
|
0,7600 |
1 |
0,002 |
1,0000 |
||||||
|
100 |
|||||||||
Сравнение гистограммы и нормальной кривой наглядно показывает согласованность между теоретическим и эмпирическим распределением.
Примечание: Построенные графики находятся в приложениях к работе.
6* Проверить гипотезу о нормальном законе распределения по критерию согласи яПирсона f^2).
Проверка гипотез о нормальном законе распределения
Частоты для проверки соответствия эмпирического ряда распределения нормальному закону используют критерий X^2, основанный на сравнении эмпирических частот mi с теоретическими m^тi, которые можно ожидать при принятии определенной нулевой гипотезы.
Значение X^2набл. – наблюдаемое значение критерия, полученное по результатам наблюдений, равно
к


 F^2набл.= (mi-m^тi)
F^2набл.= (mi-m^тi)

 I=1 m^i
I=1 m^i
Где к – число интервалов (после объединения).M^i – теоретические частоты. Все вспомогательные расчеты, необходимые для вычисления f^2, сведем в таблицу 1.6.
Таблица 1.6.
Вычисление критерия X^2 при проверке нормальности продолжительности горения электролампочек
|
Интервалы |
Mi(Практ) |
Mi(теор) |
(Mi-Mi(теор))^2 |
…../Mi(теор) |
||
|
a(i) |
b(i) |
|||||
|
730,644 |
735,356 |
2 |
2 |
9 |
1,29 |
|
|
735,356 |
740,068 |
8 |
5 |
|||
|
740,068 |
744,780 |
6 |
13 |
49 |
3,88 |
|
|
744,780 |
749,492 |
18 |
21 |
9 |
0,43 |
|
|
749,492 |
754,204 |
35 |
25 |
100 |
4,01 |
|
|
754,204 |
758,916 |
12 |
21 |
81 |
3,89 |
|
|
758,916 |
763,628 |
11 |
12 |
1 |
0,08 |
|
|
763,628 |
768,340 |
6 |
5 |
1 |
0,14 |
|
|
768,340 |
773,052 |
2 |
2 |
|||
|
X^2набл |
13,71 |
|||||
Правило проверки гипотезы заключается в следующем. Определяем по таблице распределения xu-квадрат критическое значение X^2кр.(альфа для числа степеной свободы V=к-3 и заданного уровня значимости альфа. Затем сравниваем X^2кр.
Если X^2 набл.<=X^2кр. , то выдвинутая гипотеза о законе распределения не отвергается(не противоречит опытным данным).
Если X^2 набл. >X^2кр. , то выдвинутая гипотеза о нормальном законе распределения отвергается с вероятностью ошибки a.
Для нашего примера X^2набл.=13,71, a=0,005, V=7-3=4 (число интервалов после объединения стало равным 7) и X^2кр. (0,005; 4) =14,9
Так как X^2набл.