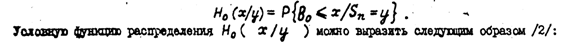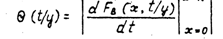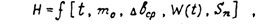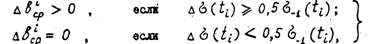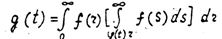Физико-статистическая оценка ресурса теплообменных труб с начальными дефектами производства в виде трещин
| Загрузить архив: | |
| Файл: 021-0004.zip (55kb [zip], Скачиваний: 74) скачать |
ФИЗИКО-СТАТИСТИЧЕСКАЯ ОЦЕНКА РЕСУРСА ТЕПЛООБМЕННЫХ ТРУБ С НАЧАЛЬНЫМИ ДЕФЕКТАМИ ПРОИЗВОДСТВА В ВИДЕ ТРЕЩИН .
В настоящее время при конструировании и разработке энергетического оборудования, в частности парогенераторов для быстрых реакторов большой мощности возникает задача прогнозирования уровня надежности элементов и узлов этого оборудования. Как показывает опыт эксплуатации, одним из основных видов отказа парогенератора "натрий - вода" является течь воды в натрий, которая возникает после образования сквозной трещины в поверхности теплообмена. С этой точки зрения, в качестве основного процесса отказа целесообразно выбрать рост усталостной трещины в теплообменной трубке парогенератора "натрий – вода”, возникшей на месте начального дефекта производства трещиноподобного типа присутствовавшего в материале трубки. Очевидно, что критерием отказа в этом случае будет появление сквозной трещины в стенке теплообменной трубки.
Для определения характеристик надежности в этих условиях на этапе проектно-конструкторской разработки предлагается использовать математическую модель, а именно зависимость вида

(1)
где Н - показатель надежности, являющийся Функцией следующих аргументов:t - время;b0 -начальное повреждение материала трубки;G - нагрузка; Мф - масштабный фактор.
Модель должна соответствовать
следующим требованиям: иметь простую структуру; содержать небольшоечисло основных значимых параметров; позволять
физическую интерпретацию полученных зависимостейдолжна быть пригодной для прогнозирования
срока службы изделия. В основе модели лежит предположение о том, что
поверхность теплообмена трубки площадью Sn , содержит начальные дефекты
эллиптической формы, расположенные перпендикулярно к первичным окружным
напряжениям. В связи с тем, что трубка представляет собой
тонкостенный сосуд давления, поверхностные дефекты подобного расположения,
формы и ориентации наиболее склонны к развитию . В процессе эксплуатации дефект
растет по глубине, оставаясь геометрически подобной фигурой. Глубина начального
дефекта В0является
случайной величиной. Введем условную функцию распределенияH0(x/y), которая представляет собой
вероятность того, что на поверхности площадью Sn=y существует дефект глубина
которого В0,
(2) где
к
,р - опытные константы. Поддействием циклических знакопеременных термонапряжений, действующих на поверхности теплообменной
трубки при эксплуатации парогенератора "натрий - вода" начальный
дефект прорастает по глубине. Рост глубины дефекта во
времени полагаем нестационарным случайным процессомB(t)основными характеристиками которого считаем функцию
математического ожиданиияmb(t)и функцию распределения Fb(x,t)
в сечении случайного процесса. В общем виде виде эти
характеристики можно определять исходя из некоторых положений линейной
механики разрушения. Известно, что все многообразие интегральных кривых
роста трещины в зависимости от наработки
могло свести к четырем формам ,
одной из которых, наиболее приемлемой в данном случав, является криволинейная
кривая прогрессирующего типа. Поэтому очевидно, что mb ( t ) является нелинейной функцией времени
параболического вида. При этом необходимо также учитывать, что процесс роста
трещины идет скачкообразно. Исходя из вышеуказанных соображений, предлагается в
качестве функции математического ожидания mb ( t ) процессаB ( t ) выбрать следующую зависимость:
(3) где m0 математическое ожидание глубины начального дефектаB0; Dbср - средняя величина скачка трещины;W (t) - неубывающая
функция времени, представляющая собой число скачков трещины в единицу времени. Таким образом, в
выражения (3) Dbср представляет средний размер скачка трещины, а
произведениеW
( t ) tопределяет число таких скачков за времяt . Считаем, что распределение размера трещины в
фиксированный момент времени t полностью определяется условнымм
распределением начальных дефектовН0(x/y). Тогда Из
выражения (2) получаем Исходя из
данного выше критерия отказа, под вероятностью отказа Q ( t )телообменной трубки
следует понимать вероятность пересечения нестационарным случайным процессом В ( t ) Фиксированного уровняh . где h - толщина
стенки трубки. Для определения Q ( t )необходимо определять условную плотность
распределения времени до пересечения фиксированной границы Q ( t /y):
Тогда
(4) Таким
образом, выражение (1) для показателя надежности Н можно представить в
следующемвиде: гдеm0 - математическое ожидание глубины начального дефекта,
характеризующее начальное повреждение
материала трубки;Dbср иW(t)
определяются условиями нагруженияG ; Snопределяется размерами трубкиMф. Рассмотрим
вопрос об определении этих параметров. Математическое
ожидание глубины начального дефекта m0
определяется с помощью операции повторного математического ожидания с
использованием выражения (2) m0=M[M(b0/y)]
(5) Константы К и P в выражении (2)
определяются с помощью статистической обработки результатов дефектоскопических
исследований материалов и узлов
парогенератора "натрий - вода" при его изготовлении и испытаниях.
Естественно, что на этапе проектирования данной конкретной конструкции таких
данных может и не быть, но дело в том, что размеры начальных дефектов не связаны
непосредственно с типом конструкции, а в основном зависят от материала
элементов и условий их изготовления и обработки. Поэтому набор статистики для
определения К и P не
представляет принципиальных трудностей. Для определения параметра Dbсрможно
воспользоваться известными соотношениями для скорости роста усталостной трещины
, методом моделирования или экспериментальными методами. Для определения
параметраW(t) - интенсивности скачков трещины -
воспользуемся условием роста усталостной трещины в металле при циклическом нагружении:
(6) где Dbср -
величина i -госкачка трещины; Ds ( ti ) - амплитуда действующего напряжения
в момент времениti ;
s-1(ti) - значение предела выносливости в момент ti. Поведение
предела выносливости во времени можно описать случайной функцией времени s-1 (t), которая
представляет собой произведение случайной величины s-1на неслучайную
функции времени j(t),
называемую функцией усталости Функцию усталости естественно считать непрерывной
монотонно убывавшей функцией, такой, что и
определенной при всех t
> 0 . Амплитуду нагрузки
Ds ( t ) во времени считаем стационарным случайным процессом
с нулевым математическим ожиданием и
ненулевой дисперсией. Таким образом, для определения W ( t ) необходимо определить число пересеченхй
в единицу времени стационарного случайного процесса со .случайной функциейs-1 ( t ). Вероятность пересечения g ( t )
можно выразить следующим образом : где f (r ) ,f (s
) - плотность
вероятности в сечениях s-1( t ) иDs ( t ) соответственно.
Тогда
(7) В заключение следует отмеить, что
исходя из предложенной модели надежности можно рассмотреть примерную методику расчета
характеристик надежности трубки теплообмена на этапе проектирования: 1) получение исходной информации об условиях эксплуатации, начальных
дефектах и харахтеристиках материала трубки; 2) Выделение наиболее "опасных" в надежностном отношении сечений трубки, т.е. тех участков поверхности теплообмена,
где сочетание эксплуатационных и конструкционных факторов наиболее
благоприятствует зарождению и развитию усталостных трещин; 3) определение параметров модели для каждого из
сечений по формулам (5), (7); 4) расчет характеристик надежности трубки для
каждого сечения на основе формулы (4); 5) расчет характеристик надежности трубки в целом,
исходя из того, что появления сквозных трещин различных сечениях трубки
являются независимыми событиями.
Список литературы: 1. ВессалЭ. Расчеты
стальных конструкций с крупными оечениями методами
механики раврушения.-В кн.: Новые методы оценки
сопротивления металлов хрупкому. разрушению. М.: Мир, 1972. 2. Миллер А. и др. Коррозионное растрескивание циркаллоя под
воздействием йода. - Атомная техника за рубежом, 1984, № 2, с.35. 3. Волков Д.П., Николаев С.Н.
Надежность строительных машин и оборудования. М.: Высшая школа,1979. 4. Острейковскнй В.А. Многофакторные испытания на надежность. Ц.: Энергия, 1978. 5. Острейковский
В.А., Савин В.Н. Оценка надежности трубок прямоточного теплообмена. -Известия ВУЗов. Сер. Машиностроение, 1984, № 2, с. 47. 6. Гулина O.М., Острейковский В.А.
Аналитические зависимости для оценки надежности с учетом корреляции между
нагрузкой и несущей способностью объекта, - Надежность и контроль качества, 1981. №2б, c.36.