Лекции по физике за 3 семестр

Сдавался/использовался	2000г., Москва, МАИ
Примечание	Лекции очень хорошие, записано буквально ВСЁ ! Читал: Бабетский В.И.
	Загрузить архив:
	Файл: 041-0010.zip (893kb [zip], Скачиваний: 159) скачать

Лекции по физике

Владимира Иннокентьевича Бабецкого

(III семестр физики на факультете "Прикладная математика и физика" МАИ) 2000г.

§1. Введение

Вот то, что кончилось у нас в прошлом семестре, в исторической перспективе это физика на конец XIX и начало XXвека, и эта физика стала называться классической. А вот дальше – в XX веке – появилась новая физика, не то, что новые главы, она по существу другая. И в этот семестр у нас фактически войдёт всё, что создано в ХХ веке.

И тут дело не просто во временной последовательности, – важно то, что эта физика качественно другая. Проблема в том, что классическая физика оказалась не в состоянии объяснить, как устроен окружающий нас мир. Ну, кое-что, конечно, есть: паровые машины, электричество, радио – вся эта техника была создана на базе этой физики, но глубинные свойства окружающего мира (вот не то, что вы создали руками, а именно, что вот здесь вокруг) казались за пределами понимания современников.

Простой пример. Теплота, молекулярная физика используют свободные атомы: вот в воздухе носятся атомы, точнее молекулы. Все тепловые явления кинетическая теория, в частности теплопроводность, теплоёмкость, прекрасно объясняет, но если копнуть глубже, то там мы сталкиваемся с вещами необъяснимыми. Молекулы воздуха сейчас сталкиваются тут всё время, число столкновений в секунду колоссальное, и что? Скажем, сталкиваются молекулы кислорода, разлетаются, сталкиваются, разлетаются, сталкиваются... И они остаются теми же самыми, а молекула – это некоторая структура, это не просто там какой-то мифически неделимый объект (именно такое понятие скрывалось за словом атом в древности, атом – неделимый), уже ясно было, что это объект, обладающий структурой: в атоме есть электрон, позитрон, – механическая система. Почему же эти атомы сталкиваются, и всё время остаются тождественными себе, они не несут на себе никаких следов их предыдущей жизни? Факт, конечно, необъяснимый. Сталкиваются два автомобиля, и, конечно, они несут на себе следы столкновения, а если они будут сталкиваться ежесекундно, в конце концов, получится совсем не то, что было вначале, и это всё понятно, почему же на атоме не остаётся следов? Можно этот атом разбить вдребезги, но потом из этих осколков может опять слепиться этот атом, тот же самый. Это, казалось бы, находится в ведении обычной механики: существует система частиц (в атоме не так их много). Вот, солнечная система, – механика всё это дело объясняет, но стабильность атомных структур и стабильность структур, тогда уже построенных из атомов (то, что мы видим вокруг себя стабильно в известных пределах), не изменяющийся, устойчивый мир – это не прописано в классической физике. В классической физике параметры любой системы могут принимать любые значения, эти параметры подвластны внешним воздействиям.

Есть, например, солнечная система, механику Ньютон придумал, и он же придумал формулу для силы взаимодействия, и понеслось. Функционирование этой системы было понято, можно было делать предсказания на 1000 лет вперёд, на 1000 лет назад. Например, специалисты в небесной механике могут вычислить все солнечные затмения, которые происходили 1000 лет назад, это так и делается для хроников: есть сообщения, что там было такое-то явление природы и прочее.1)

Вот такая система: Земля вращается вокруг Солнца на расстоянии 150 миллионов км, другие планеты имеют свои параметры орбит. Почему? А не почему – начальные условия. Когда-то это дело всё затикало.2) Пролетела бы где-нибудь сравнительно близко от этой солнечной системы другая звезда, – всё бы это возмутилось: параметры орбит стали бы другими, система претерпела бы определённые пертурбации (их можно было бы рассчитать и предсказать), мы получили бы другую систему. Атом не так! Скажем, планетарная модель атома: есть ядро, электроны, валентность, – но его свойства не меняются не то, что там где-то вблизи пролетел, а именно колоссальное число столкновений, которые происходят сейчас здесь за секунду, не меняет этих характеристик.

Я ещё раз обращаю внимание, что этот факт не подпадает под юрисдикцию классической физики, нет в ней таких механизмов, которые позволили бы объяснить эту зависимость.

Дальше, например, генетический код. Организм вырастает из клетки, понятно, что должен быть план, по которому организм развивается, и этот план должен иметь материальный носитель. Есть материальный носитель, скажем, молекула ДНК, гигантская молекула длиной порядка 3м, она в клетке свёртывается в спираль, это линейная конфигурация макроскопических размеров, там записан этот код. Какова должна быть стабильность записи этого кода, что на протяжении тысяч поколений информация не теряется! Все вы знакомы с носителями информации, и, конечно, есть устойчивые носители, скажем там цифровая запись, но вот более старый носитель информации – виниловые нити (в аналоговых машинах), – информация плывёт, понятно, что нити крутятся, крутятся, крутятся, и постепенно возникают мелкие искажения, и делаются всё хуже и хуже. С генетическим кодом ничего такого не получается. Есть там крупные поломки, иногда рождаются уродцы, но это редкие случаи. Вообще-то, на протяжении тысяч поколений сохраняется этот код.

Классическая физика не предусматривает никаких механизмов поддержания такой стабильности. Если вы пороетесь в памяти, любая макроскопическая система, и системы, на которых мы упражнялись и которые описываются классической физикой, обладают тем свойством, что малые внешние воздействия вызывают малые изменения параметров системы, то есть всякая система может плавно менять свои параметры, а вот такие устойчивые структуры не прописаны там.

Это я клоню именно к тому, что на самом деле всё, что мы до сих пор изучали, не позволяет понять, как же всё-таки устроен окружающий мир, почему он имеет такие свойства, какие имеет.

Ну, и вот то, чем мы будем заниматься в течение семестра, – изучать, как физика ответила на этот вызов, и каким образом всё-таки удалось (а это действительно удалось) понять, как устроен этот мир.

И сразу скажу, между прочим, что на уровне наблюдаемых явлений в масштабах Земли и то, что сейчас творится на небе, на этом уровне физика сейчас проблем не имеет, то есть все эти наблюдаемые свойства, полученные здесь, не представляют собой загадки и исчерпывающим образом на этом уровне описываются. Есть проблемы на более фундаментальном уровне – вглубь вещества – не на уровне атомов, молекул, ядер, а ещё гораздо глубже, то есть вот поведение на таком более глубоком уровне там да есть проблемы, но тот уровень не проявляется в наблюдаемом физическом мире, тот глубинный уровень не проявляется. Он был существенен на самых ранних этапах возникновения Вселенной, и там действительно есть проблемы, которые не решены ещё, но повторяю, это проблемы на том уровне, который не влияет практически на то, что мы видим вокруг (то, что мы видим вокруг, там проблем нет, тут физическая теория практически дошла до предела).

Но так глубоко мы здесь не закопаемся, а вот устройство мира на уровне атомов, молекул, твёрдых тел, вот эти вещи мы здесь с вами разберём и поймём, в глубь элементарных частиц мы не залезем и те глубинные вещи затрагивать практически не будем.

Вот такая программа действий. Так, ладно, это лирика была, а теперь перейдём к делу.

§2. Взаимодействие света с веществом. Корпускулярные свойства света

1) На самом деле, взаимодействие света с веществом не описывается в рамках вот этого представления о свете как об электромагнитных волнах. Ну и коротко обсудим известную вам вещь – фотоэффект.

1) Ну, понятно почему. Допустим, быстрые молекулы улетели вот из этого хвоста распределения, но хвост отрастает всё время, если температура остаётся та же самая, хвост отрастает, и поэтому, в конце концов, они испарятся все.

Если теперь вернуться к вопросу о том, почему не вылетают электроны из металла, возникает такая проблема: если электроны в металле как частицы идеального газа, то среди них должны быть энергичные электроны, которые всё равно вылетят, эту работу совершат и улетят. Должно происходить непрерывное испарение электронов из металла. В чём бы это проявилось? Это проявилось бы в том, что кусок металла имел бы положительный заряд, а это тоже проявилось бы на бытовом уровне, и можете легко сообразить в чём. На любой кусок металла налипала бы всякая мелочь, пыль, бумажки, он был бы облеплен всякой гадостью, любой кусок металла должен был бы быть облеплен пылью больше, чем соседний кусок дерева. Этого не наблюдается. Это означает, что электроны не испаряются. А это означает, что функция распределения по энергиям внутри металлов такая, как на рис.1.4. Был бы «хвост» у этой функции распределения, – электроны бы испарялись, и кусок был бы облеплен. Вот, между прочим, первое обстоятельство, которое говорит, что здесь что-то не то с нашими представлениями. Действительно, функция распределения по энергии электронов в металле имеет вид не такой, как на рис.1.3, а такой. Имеется некоторая энергия . Если взять интервал энергии

Тот факт, что металл не облеплен пылью, говорит, что нет хвоста, то, что обрыв такой резкий, из этого сказать нельзя, но где-то эта функция должна оборваться.

Если рисовать потенциальную энергию электронов в металле, то это можно изобразить так: вне металла уровень постоянный, там нет электрического поля, а внутри металла потенциальная энергия падает.Это соответствует тому, что в этой области действует сила , затягивающая электроны, внутри электрон опять свободен, сила на него не действует, и внутри потенциальная энергия снова постоянна. Вот такая картина потенциальной энергии (рис.1.5).

Полная энергия электрона это сумма потенциальной и кинетической энергии. Если я нарисую Е – для свободного электрона. Самому  энергичному электрону (который имеет максимальную кинетическую энергию) внутри металла, чтобы допрыгнуть до края ямы, не хватает куска работа выхода.1) Почему может вылетать электрон при освещении светом?

Могут сказать, ничего удивительного нет. Свет это электромагнитная волна, она проникает в металл, в ней есть меняющееся электрическое поле, на электрон действует сила, электромагнитная волна может сообщить ему достаточную энергию, и, если ему повезёт, что с этой энергией он будет иметь направление импульса на границе металла в вакуум, то он вылетит. В этом смысле ничего удивительного нет, всё нормально. Тогда следовало бы ожидать, что чем больше интенсивность падающего света, то есть чем больше амплитуда волны, тем с большими скоростями будут вылетать электроны из металла, потому что тем большую энергию они могут получить от этой волны. И тут первая осечка – на самом деле, не влияет интенсивность света на скорости, с которыми вылетают электроны. Оказалось, что на это влияет характеристика света, совсем вроде бы не имеющая отношения к делу, а именно, частота. Скорость вылетающего электрона зависит не от падающей энергии, а от цвета. Если на металл направить синий свет, то электроны будут вылетать с большими скоростями чем, если светить красным, если светить светом с ещё меньшей длиной волны, то они вообще не будут вылетать, какая бы ни была интенсивность. Вот, это были экспериментальные факты по фотоэффекту, и на этом забуксовала вся наука, которую мы с вами до этих пор изучали.

Вот первый пример, на котором споткнулась теория.2) Были и другие проблемы, тоже на первый взгляд невзрачные, но не находящие решения в рамках этой самой теории, но это была очень внятная не решаемая проблема.

Для решения такого рода проблем пришлось отказаться от волновой теории и признать, что при взаимодействии с веществом свет ведёт себя как поток частиц, то есть вернуться к старым корпускулярным представлениям, которые ещё Ньютон разделял.3)

Чем же отличаются волны и частицы? Светим на кусок металла источником монохроматического света с определённой длиной волны, например зелёным. Измеряем скорости, с которыми вылетают электроны, оказывается, эти скорости меняются в пределах от нуля до некоторой максимальной скорости. Считаем, сколько электронов вылетает в секунду. Когда мы удаляемся от источника, свет делается более тусклым, скорость, с которой вылетают электроны, не зависит от расстояния, число вылетающих электронов зависит. Взрывается бомба, идёт в воздухе ударная волна, её энергия убывает как

Если иметь в виду эту аналогию, то понятно, что свет при фотоэффекте ведёт себя как частица, как летящая пуля: как бы далеко это движение не удалялось от источника, если произошло взаимодействие, то электрон вылетит с той же самой скоростью. То есть эффект взаимодействия от расстояния не зависит; вопрос заменяет вероятность того, что свет провзаимодействует с электроном. Именно это и говорит, что при фотоэффекте свет ведёт себя не как волна, энергия которой убывает как взаимодействие света с веществом происходит так же, как, если бы он был потоком частиц. Эти частицы получили название фотоны.

Энергия фотона связана с частотой. То, что мы в волновой теории называли частотой, а просто визуально это проявляется в цвете, эта вещь определяет энергию фотона: h – постоянная Планка. Она появилась немного раньше и по другим причинам (как она появилась, мы это в своё время обсудим). h – это некоторая константа с размерностью действием. Импульс фотона – это энергия, делённая на скорость света: p= 0),

Когда в квантовой механике говорят о частице, то образ объекта локализованного в пространстве и обладающего определёнными свойствами оказывается неверным. Частица – это носитель некоторых определённых свойств, например, объект с массой покоя 10^-13кг, зарядом, равным заряду электрона, со спином ½ (есть такая характеристика) называется электроном и рассматривается как частица. Частица классически – локализованный объект, являющийся носителем свойств. В квантовой механике свойства остаются, носители исчезают. «Алису в стране чудес» кто читал, знают, на дереве сидел улыбающийся кот, а потом он начал исчезать, растворяться, и исчез, и осталась одна улыбка. С понятием частицы произошло то же самое: классическая частица (кот) исчезла, растворилась, а её свойства (улыбка) остались. Вот в квантовой механике оперируем именно этими улыбками без кота, на самом деле, физике этого достаточно.

Фотон – это частица, для которой масса равна нулю, и для фотона Е тоже будет порядка 1)

Я начал с того, есть ли ещё частицы, которые имеют массу, равную нулю, и, стало быть, движутся со скоростью света. Похоже, что нет. Долгое время претендентом на то было нейтрино, и сначала с уверенностью считали, что масса нейтрино ноль, потом, лет 20 назад, возникли сомнения: масса близка к нулю (измерения давали массу порядка 10эВ), но вопрос до сих пор повис. Неясно равна нулю масса нейтрино или нет, других претендентов вообще нет, поэтому фотон пока единственная частица с массой равной нулю. Конечно, трудно себе представить, что это за частица с массой ноль. На самом деле особо не надо напрягаться: мы не можем её взять в руки, фотон всегда будет носиться относительно нас со скоростью света, а если нельзя взять в руку, то нет смысла думать о том, как понимать массу этой частицы.

можно написать следующее:

Фотон это частица, у которой масса равна нулю или, чтобы не было недоразумений, масса покоя равна нулю. Частица с нулевой массой обязана двигаться со скоростью света в любой системе отсчёта. Будете ли убегать от неё, всё равно её скорость равна скорости света.2)

2

Имеются такие явления, для которых свет демонстрирует волновые свойства (дифракция, интерференция), имеются явления, когда он демонстрирует корпускулярные свойства (например, фотоэффект), возникает естественный вопрос, что же он такое на самом деле, волна или частицы? Кто был прав, Ньютон или Гюйгенс, которые придерживались на первый взгляд взаимоисключающих точек зрения? Ответ такой – вопрос, что он такое на самом деле, предполагает ответ из двух взаимоисключающих альтернатив, или он естьто, или другое, или он есть ни то и ни другое. Это означает, что свет более сложный объект, чем можно было себе представлять. Тут надо иметь в виду вот что: понятия «волна» и «частица» это наши изделия, мы пытаемся описать мир в понятиях, которые мы придумали, удачно или неудачно. Неудачные вымирают, удачные же остаются, но надо иметь в виду, что это всегда наши понятия, и, в общем-то, они могут оказаться более сложными и не укладываться в рамки, в которые мы пытаемся их запихнуть с помощью языка.

Приведём пример. Скажем, у нас два слова: мы знаем, что такое стол, и мы знаем, что такое стул. Кто-то приходит и раз – ставит табуретку, и спрашивает, что это такое. Четыре ножки, ровная поверхность – это стол, с другой стороны на ней сидят – это стул. На самом деле это не стол и не стул, а, так сказать, по потребности может быть и тем и другим. Значит, какой выход? Надо придуматьспециально новое слово «табуретка».

Оказалось, что реальность не делится на классы понятий волны и частицы, мы дальше увидим, что положение ещё более драматично. Поскольку нового слова для такого объекта как свет ещё не придумали, приходится пользоваться такими выражениями, что в некоторых ситуациях свет ведёт себя как волна, в некоторых как частица. Важно, чтобы эти ситуации были действительно различными.1) Имеется чётко ограниченный круг явлений, когда объект проявляет корпускулярные свойства, и вполне определённые ситуации, когда объект проявляет волновые свойства. 2)  Никаких проблем нет.

Конечно, должен быть соответствующий математический аппарат и математическая теория, которая позволяет давать ответы на соответствующие вопросы. Повторяю, дальше, когда мы будем рассматривать квантовую теорию, там мы будем сталкиваться с ещё более удивительными и драматическими проявлениями вот этой дилеммы волна – частица.

Закончим рассмотрение фотоэффекта. Напомню, на металл падает свет, из металла вылетают электроны, тогда это иллюстрируется такой энергетической диаграммой (рис.1.5).

Если в металл проникает фотон,3) имеющий энергию большую, чем работа выхода, то электрон вылетит из металла, и избыток энергии пойдёт на его кинетическую энергию, и мы тогда видим, что

Это знаменитая формула Эйнштейна. Эйнштейн в 1921 году получил Нобелевскую премию за это, не за теорию относительности, а вот за эту вещь, которую теперь может написать любой школьник. Казалось бы за что премия? Вот за то, что надо было осознать, что свет может представляться как поток частиц, корпускул, отказаться от господствующей точки зрения.

Видно, что если энергия фотона меньше работы выхода, электрон её поглотил, подскочил и всё равно из ямы не выскочил, фотоэффект не происходит. Если металл освещать светом с частотами меньше, чем 4)

Куда деваются фотоны, когда они выбивают электроны? Фотоны отличаются от пуль тем, что для них нет закона сохранения частиц: вот, родился фотон, он не сидел в атоме, как пуля в ружье, потом поглотился другим атомом и исчез.

Куда деваются электроны, когда их выбивают фотоны? Имеем кусок металла, светим на него из фонаря, из металла вылетают электроны, сколько их вылетает и до каких пор они будут вылетать?Когда какое-то количество электронов вылетело и ушло на бесконечность (если у нас один шар на свете и больше ничего нет), то, металл приобретёт положительный заряд, и, в конце концов, этот заряд станет настолько большим, что максимальной кинетической энергии, с которой вылетает электрон, не хватит, чтобы уйти на бесконечность. Что тогда будет происходить? Электрон вылетел и летит обратно. Это означает, что всякий кусок металла при освещении должен иметь некоторый положительный заряд, и он окружён облаком электронов, которые вылетают и затягиваются обратно.

1) Нас будет интересовать частота в виде функции от угла рассеивания

От угла мы можем избавиться, возведя последние два уравнения в квадрат и сложив их:

выразим

Это мы нашли импульс рассеянного фотона, выраженный через импульс налетающего фотона и угол рассеивания фотона.

И здесь сразу можно усмотреть, почему неправильная была предъявлена теория «Почему небо синее?», вам на экзамене её приходилось отвечать, почему она, тем не менее, могла быть? По корпускулярной теории частота рассеянного света должна быть меньше частоты падающего, а по волновой они одинаковы. Видно, что, если

Действительно, были проделаны эксперименты,1) и эта формула подтвердилась. Эффект Комптона подтвердил корпускулярные свойства света.

1)

§3. Тепловое излучение

1. Абсолютно чёрное тело

2. Закон Кирхгофа

3. Закон Вина

4. Закон С2)

1) Значит, если это энергия, излучаемая в интервале называется спектральной плотностью излучения.2) Эта функция характеризует каждое тело. Любое тело имеет свои предпочтения: на одной длине волны излучает больше, на другой меньше, это зависит от его конкретного устройства.

Имеется другая важная характеристика – монохроматическая поглощательная способность, определяется так:

Для идеального зеркала, которое отражает всё падающее излучение на всех длинах волн, определяет абсолютно чёрное тело, такие тела есть.

3

Мы остановились на том, что абсолютно чёрное тело это тело, для которого на всех длинах волн, то есть оно поглощает всё падающее на него извне излучение и его не отражает. Мы видим определённые тела вследствие того, что мы видим отражённый от них свет, то есть мы видим отражённые электромагнитные волны,3) а если тело ничего не отражает, то, конечно, оно будет чёрным. Скажем, здесь сейчас кто-нибудь из вас стал бы абсолютно чёрным, как бы это воспринималось? А вот такой контур абсолютно чёрный без всяких деталей.4)

Для света нет материальных объектов абсолютно прозрачных, а вот для нейтрино, например, практически всё абсолютно прозрачно.1)

Есть природный объект, чёрная дыра, который является чёрным в этом смысле: всё, что на дыру падает извне, и вещество, и излучение, падает туда совершенно необратимо и безысходно.2) Но не надо таких экзотических объектов, чтобы реализовать абсолютно чёрное тело. Полость с маленькой дыркой даёт возможность реализовать абсолютно чёрное тело, а именно, вот эта поверхность дырки в полости ведёт себя как абсолютно чёрное тело по понятной причине: сюда заходит какое-то излучение, дальше оно испытывает там многократное отражение и выйдет обратно ничтожная часть того, что туда зашло, потому что при каждом взаимодействии со стенкой излучение поглощается. Окно в доме чёрное (без стекла, застеклённые окна отражают), если оно маленькое и помещение там большое. Так что абсолютно чёрное тело реализуемо.

3)

Более наглядно тут можно такой привести пример. Скажем, имеем полость зеркальную, стенки которой отражают всё падающее на них излучение, не меняя спектрального состава. Запустим туда световой луч, например, красного цвета и захлопнем дверцу. Он там начнёт метаться, и, конечно, вся эта полость будет заполнена красным светом. А теперь представьте следующее: этот ящик заполнен красным светом, и мы туда кинем маленькую пылинку, что будет происходить?  Эта пылинка начнёт нагреваться и переизлучать, она поглощает монохроматический свет с определённой длиной волны, а излучает «кашу» (она излучает во всём спектре). В конце концов, процесс размазывания энергии по частотам завершится, и мы получим равновесное излучение, которое в дальнейшем не меняется, и его спектральный состав не зависит от того, какая там была пылинка.

Есть универсальная функция, мы её обозначим спектральной плотностью равновесного излучения, равновесное излучение в любой полости будет описываться вот этой функцией. Что означают слова «спектральная плотность»? То, что энергия, которая приходится на интервал

А теперь мы хотим получить закон Кирхгофа. Рассмотрим в полости площадку величиной Подставляя выражение для падающей энергии в равенство поглощаемая и излучаемая энергии равны, следовательно, или

Что это означает? это спектральная плотность излучения конкретного материала стенок, это функция, характеризующая, опять же, материал стенок. Для разных тел эти функции различны, но их отношение, оказывается, не зависит от тела и представляется некоторой универсальной функцией. Это означает, что, чем тело больше поглощает при температуре T на длине волны λ, тем оно больше излучает при данных температуре и длине волны. Если задуматься, этот закон очень удивительный. Излучение идёт, вроде бы, из всего тела (это излучение атомов среды), а поглощение, оно, вроде бы, связано с поверхностью,1) и то, что отношение этих величин не зависит от природы тела, от характера поверхности, конечно, удивительно.2) Закон не учитывает никаких деталей, он просто основан на законе сохранения энергии, его справедливость безусловна. Мало есть законов такой мощности и общности.

Мы теперь можем осознать, что представляет собой эта функция . Если , то для абсолютно чёрного тела мы получаем , и это позволяет проинтерпретировать спектральную плотность равновесного излучения в полости: спектральная плотность равновесного излучения в полости это монохроматическая излучательная способность абсолютно чёрного тела.

1)

Я уже говорил, что получить для произвольного тела теоретически монохроматическую излучательную способность, то есть спектральную плотность вот этого стола, например, невозможно, реальные тела устроены очень сложно, чтобы теория там могла работать, а получить теоретически функцию , конечно, теория должна.2)

Мы её получим дальше, а сейчас я просто приведу её вид.

Температура T₂ больше T₁, с ростом температуры эта функция растёт (на всех длинах волн излучение увеличивается), но максимум съезжает в область коротких волн.3) Длина волны λ_max очень просто зависит от температуры: закон Вина

При повышении температуры длина волны, на которую приходится максимум, смещается.4)

1) Классическая механика неприменима в этой области.

§4. Волновые свойства частиц

Проведём мысленный эксперимент. Пусть у нас имеется экран, в экране щель, на эту щель падает поток частиц (для определённости электронов),2) на пути этого пучка ставим непрозрачный экран со щелью, а за ним ставим другой экран, на котором регистрируются попадания электронов.3) Если пучок достаточной интенсивности, то мы будем наблюдать вот такое распределение интенсивности свечения (рис.1.а). Если электроны пускать поштучно, наберём статистику, получим вот такое распределение, пока всё нормально.

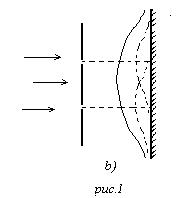
А дальше мы делаем вот что: ставим две щели, что надо ожидать? От одной щели получаем такое распределение, от другой тоже, они накладываются, и ожидаемая картина такая (рис.1.b).

На самом деле, ничего подобного. Если мы поставим две щели, ожидаемая картина рис.1.b, а на самом деле мы получим вот такую картину распределения от двух щелей (рис.1.с).

Что тут удивительного? А удивительно вот что: в эту точку 1) от одной открытой щели они попадают, если её закрыть, другую оставить, от другой они сюда тоже попадают, открываем две щели – не попадают. От каждой попадают, от двух щелей не попадают, это, конечно, уже удивительное обстоятельство. Можно подумать, что эти пучки электронов от двух щелей как-то хитро взаимодействуют друг с другом и дают такое диковатое распределение. Можно проверить взаимодействуют или нет: пучок электронов можно сделать очень слабым, ну, поштучно пропускать (один пустили и ждём, другой пустили и ждём…), тогда мы будем регистрировать на экране одиночные акты попадания (тут выпала точка, тут выпала точка…). Будет следующее: если они летят поштучно при открытой верхней щели, а нижней закрытой, мы получим, наберя статистику, вот такое распределение (рис.1.a), закроем верхнюю щель, откроем нижнюю, получим такое же распределение, откроем обе щели – опять такое (рис.1.с).

Он летит один, – если открыты две щели, он сюда (см. примечание 1) никогда не попадёт, открыта одна щель, он сюда попадёт. Тогда спрашивается, откуда он, подлец, знает, что делается со второй щелью, открыта она или закрыта она, или он проходит одновременно через две щели, раздваивается? Тоже можно проверить, как проверить? В принципе, можно наблюдать прохождение частицы через щель (грубо говоря, в микроскоп). Посадим двух наблюдателей, начнём поштучно пропускать электроны, тогда, если один наблюдатель кричит «есть», то другой молчит, у него нет, – электрон не раздваивается. Опять встаёт тот же вопрос, откуда он знает о второй щели? И ответ такой: вопрос снимается сам собой! Если мы здесь поставим этих соглядатаев, которые фиксируют прохождение электронов либо здесь, либо здесь, вот эта вся картина (рис.1.c) разрушается, получается вот такая (рис.1.b). Вот таково поведение частиц, и именно вот это поведение выражается словами частицы обладают волновыми свойствами. Почему волновыми? Да, потому что это типичная картина интерференции от двух щелей.

Если мы имеем две щели, то мы должны считать, что на эти щели падает волна, получается вот такая интерференционная картина (это только, если мы имеем две щели иникаких микроскопов, никаких соглядатаев, которые ловят эту частицу на месте преступления). Если мы имеем две щели с микроскопами, частица ведёт себя как частица и никакой интерференции не происходит. Это резюмируем так, что в определённых ситуациях частицы проявляют волновые свойства, то есть демонстрируют вот такую интерференционную картину, в других определённых ситуациях они ведут себя как нормальные частицы.

Ну и тогда понятно, куда же тут соваться нам с классической механикой? Никакой интерференции, конечно, классическая механика не предусматривает. Тот факт, что открыты две щели или открыта одна щель влияет на распределение частиц на экране, говорит о том, что понятие траектории неприменимо, потому что, когда идёт такое распределение, нельзя приписать электрону определённую траекторию. Потому что траектория должна была бы проходить либо здесь, либо здесь, она не может пройти одновременно через две щели, а он ведёт себя так, как будто он знает про вторую щель. Значит, понятие траектории не применимо, ну и соответственно рушится тогда вообще вся схема, которую мы изучали (классическая механика).

Для описания поведения частицы в атомарных масштабах пришлось создать совершенно другую науку. В начале девятисотых годов начало появляться такое неуютное ощущение, что с физикой что-то не в порядке, она не справляется с проблемами, и вот за четверть века всё это было решено.

1)

Если волновая функция частицы известна, то, очевидно, известно всё, что можно знать. Волновая функция исчерпывающе описывает состояние частицы, то есть может дать ответы на все разумные вопросы. Нюанс только в том, что вопросы, которые в рамках классической физики разумны, например, вопрос, где находится частица, разумный, он здесь оказывается неразумным, и ответ на него дать нельзя. Какие вопросы разумны, какие нет, мы дальше увидим по ходу дела, но в квантовой механике обнаружилось, что не на всякий вопрос, сформулированный на обыденном языке, может быть дан ответ.2) Нашей задачей будет научиться давать ответы на разумные вопросы. А пока двигаемся дальше.

§5. Уравнение Шрёдингера

1. Решение уравнения Шрёдингера для свободной частицы

2. Длина волны Дебройля (де Бройля)

3. Волновые пакеты. Соотношения неопределённостей

4. Расплывание волновых пакетов

5. Стационарные состояния

6. Прохождение частицы через потенциальный барьер. Туннельный эффект

7. Связанные состоя1) Это уравнение подтверждается тем, что теория, построенная на базе этого уравнения работает и даёт правильные предсказания для всех ситуаций, где она применима.

1) Можно положить константу равной нулю, не теряя общности, потому что потенциальная энергия определена с точностью до константы, поэтому мы положим

                                     (2)

Это уравнение в частных производных, я его не буду решать, я просто предъявлю решение, и мы убедимся, что это действительно решение. В качестве кандидата на решение выдвигаем вот такую функцию:

фазу обозначим буквой u,

2)

, а , таким образом, 3)

Подставляем то, что мы добыли, в уравнение (мы хотим убедиться, будет ли эта функция решением уравнения (2)):

Значит, функция

                                       (3)

удовлетворяет уравнению Шредингера для свободной частицы, если константы k, ω не любые, взятые с потолка, а связаны таким образом:

                                                 (4)

Забегая вперёд, дальше будет ясно почему так, а сейчас это будет голословное утверждение: Волновая функция (3) описывает частицу с энергией и с импульсом 4) означает, что действительно, так как уравнение (1) не релятивистское,

Теперь, конечно, хочется взглянуть на волновую функцию на базе тех наших смутных знаний о ней. Мы знаем, что есть вероятность обнаружить частицу, смотрим, оказывается 3) осциллирует, это бегущая волна, вроде есть движение, но функция Ψ не наблюдаема, это математическая функция, за функцией Ψне стоит никаких наблюдаемых величин, а наблюдаема не зависит от t), то есть всё наблюдаемое распределение застывшее. Конечно, одинаковая вероятность найти частицу здесь или в другом угле вселенной неприятна, уж слишком далеко это представление, но надо иметь в виду, что само решение физически не реализуемо: в электродинамике плоская волна обладала бы бесконечной энергией, но решение на самом деле очень полезно.

Математический факт такой, что беря суперпозицию этих функций со всевозможными частотами и волновыми векторами, мы можем получить все решения уравнения Шрёдингера для свободной частицы. Общее решение уравнения Шрёдингера для свободной частицы представляется в виде суперпозиции функций вида (3):

То есть задайте любой вектор 3), ω через вектор выражается, получится частное решение. Суммируя по всевозможным векторам

Мы написали общее решение уравнения. Вы, конечно, должны были удивиться: функция (3) есть решение волнового уравнения, которое выглядит так:

                                         (5)

В (2) тоже, но первая производная! Это замечательное обстоятельство – поиск комплексного решения математически приводит к тому, что уравнение (2) удовлетворяется уравнением волны, хотя, его штатная роль – быть решением уравнения (5).

1)

Мы сейчас можем понять тот эксперимент с частицами, который наблюдали в прошлый раз. Пусть у нас имеется пучок частиц с определённым импульсом, такой пучок частиц описывается функцией (3) это плоская волна, значит, мы устроим пучок частиц с определённым импульсом, частица с определённым импульсом описывается волновой функцией. Эта волна падает на экран со щелями, дальше из этих щелей выходит сферическая волна, и на экране эти волны интерферируют. Если из верхней щели идёт волна 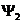A мы будем иметь:

Что такое 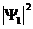A, если бы не было второй щели. Мы видели, что ожидаемый результат от наложения этих интенсивностей и дают интерференцию.

Какой длиной волны характеризуются эти функции? Число у нас связано с импульсом частицы:

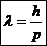                                                           (6)

называется длиной волны Дебройля.

Дебройль ещё до всей этой науки выдвинул гипотезу о том, что частице надо приписывать волновые свойства, которые характеризуются вот такой длиной волны. Наводящие соображения – это поведение фотонов (фотоны к тому времени были известны): импульс фотона равняется

определяет вероятность обнаружить частицу, а сама функция тогда называется амплитудой вероятности. Если частице приписываются волновые свойства с длиной волны

Амплитуда не наблюдаема, фаза наблюдаема, и именно фаза определяет интерференционнный результат. Если частицы проходят через две щели и мы не можем сказать, через какую щель проходят частицы, то в точке A складываются амплитуды, если мы здесь поставим микроскопы, то в точке A складываются вероятности. Это правило вводит в рамки теории тот удивительный факт, что, когда мы ставим микроскопы, то нарушается интерференционная картина. Даже можно понять, почему нарушается. Когда мы пытаемся пронаблюдать частицу в щели, а наблюдение это всегда проявляется во взаимодействии,1) надо по крайней мере идти с фонарём, чтобы её осветить, при чём осветить светом с достаточно малой длиной волны.2) Если мы хотим её фиксировать в пределах щели, то длина волны должна быть не больше, чем ширина щели. Это означает, что частота должна быть достаточно велика, а это означает, что импульс фотона достаточно большой (по крайней мере, один фотон должен рассеяться на частице и попасть нам в глаз через микроскоп), и когда этот фотон взаимодействует с частицей, то он, конечно, меняет её состояние. А к чему это приводит с точки зрения волновой картины? Когда мы электрон наблюдаем, то взаимодействие приводит к тому, что фаза волны в этой точке хаотически меняется и волны, идущие от этих щелей, перестают быть когерентными, а когда они перестают быть когерентными, то интерференционные члены дают в среднем ноль. Вот как решается эта задача со щелями.

Ну, и, наконец, последний вопрос – являются ли волновые свойства свойствами какого-то специального сорта частиц (электронов или частиц атомных масштабов)? Ответ – нет, волновые свойства присущи всем частицам. Почему же тогда классическая механика существует и мы никогда не наблюдали интерференционные явления, связанные с пулями или падающими камнями? Ответ – длина волны очень мала: ^-34м: ^-10)! Значит, волновые свойства присущи всем частицам, просто для макроскопических частиц они не наблюдаемы (по той же причине, по какой волновые свойства света не очень наблюдаемы на бытовом уровне).

1)

Беря суперпозицию синусоидальных волн, мало отличающихся друг от друга по частотам x и определённой длительностью Δt.2) Значит, можно получить такое решение [уравнения Шрёдингера], которое называется волновым пакетом. Он ограничен в пространстве и во времени.

Синусоидальная волна имеет скорость, называемую фазовой, и волновыми числами

в окрестности центрального волнового числа k₀.1)

У нас для волн, представляющих амплитуды вероятностей есть дисперсия.

И здесь мы снова подбираемся к представлению, почему возможна классическая механика. Если мы имеем решение в виде волнового пакета, это означает, что частица находится где-то в пределах волнового пакета, снаружи вероятность равна нулю, и этот волновой пакет движется с групповой скоростью

6

Мы видели, что решением уравнения Шрёдингера для свободной частицы является функция и энергией

Строго монохроматическая волна – это состояние экзотическое. Таких волн в природе нет. Дальше математический факт: общее решение уравнения Шрёдингера для свободной частицы может быть получено суперпозицией таких решений. Из теории рядов Фурье известно, что, беря суперпозицию таких синусоидальных функций, можно построить функцию отличную от нуля лишь в ограниченной области пространства и равную нулю во всём остальном пространстве, так называемый волновой пакет.

Пусть вдоль оси x идёт такой пакет пространственной протяжённости Δx и ограниченный во времени. Если частица находится в состоянии такой волновой функции (вероятность обнаружения частицы отлична от нуля где-то только в пределах этого пакета), то мы видели, что этот пакет движется с групповой скоростью

Факт математический: если мы хотим построить функцию отличную от нуля в интервале Δx, то мы должны суммировать экспоненты с различными числами k, но отношение должно быть порядка единицы: ~1. Если мы слепили этот пакет из функций с различными числами k, то это означает, что там присутствуют различные импульсы (каждому k соответствует свой импульс), значит в состоянии, которое представляется волновым пакетом, импульс не имеет определённого значения, и выполняются такие соотношения:

                                                 (7)

Интерпретация такая: Δx – неопределённость в x-ой координате, – неопределённость в x-ой составляющей импульса.Утверждается, что эти неопределённости связаны, то есть нельзя одновременно сделать их сколь угодно малыми, как бы мы не изготовляли состояния, мы никогда не добьёмся того, что неопределённости в координатах и импульсе будут сколь угодно малыми. Мы, например, можем изготовлять состояния с всё более точными значениями импульса, тогда значения координат будут делаться всё более неопределёнными. Это называется соотношения неопределённости.

Эти соотношения, так сказать, фирменный знак квантовой механики, вот, формула – это фирменный знак теории относительности, а это – квантовой механики. В этих соотношениях увязаны корпускулярные и волновые свойства. Если бы частицы вели себя так, как им предписано в классической механике, то это были бы объекты, которые имеют точное значение координат и точное значение импульса, волна не может иметь точного значения координат, волна размазана в пространстве всегда, и, значит, эти свойства частиц стыкуются более-менее вот в этих соотношениях. То есть в соотношениях (7) в концентрированном виде выражается всё это необыкновенное поведение частиц в атомных масштабах.

1) Можно оценить это расплывание.

Разброс в импульсе , этому разбросу в импульсе соответствует разброс в скоростях , где m – масса частицы, а этому разбросу скоростей будет соответствовать увеличение расстояния 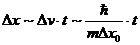x₀, то к моменту времени t он будет иметь такую длину.2)

Там, где существенны волновые свойства, там рушится понятие траектории. Мне был приведён контрпример – наблюдаются траектории в камере Вильсона. Действительно, в камере Вильсона электроны оставляют следы, как это со всем сообразуется? Сообразуется следующим образом.

Во-первых, как получается след в камере Вильсона? В чистом небе высоко где-то летит самолёт, которого почти не видно, и за ним тянется ровный белый след – рисуется его траектория. Тот же механизм и в камере Вильсона. Там на этих высотах чистая атмосфера и водяной пар, переохлаждённый водяной пар (на высоте 10000м температура порядка –40^оС). Водяной пар при таких температурах должен был бы конденсироваться, но для конденсации нужны конденсаты.1) Летит самолёт, выбрасываются частицы (сгорает топливо в двигателе), они становятся центрами конденсации и на них высаживаются капли воды, и мы получаем такую белую полосу. Камера Вильсона действует таким же образом. Под поршнем, скажем, пар, и внезапно поршень выдвигают, начинается адиабатическое охлаждение. Пар переводится в состояние охлаждённого пара, в этот момент залетает частица, она производит ионизацию атомов в воздухе, эти ионизированные атомы делаются конденсатами, на них высаживаются капли воды, мы получаем видимый след. А теперь, как это связано с теорией?

Вот у вас летит электрон это волновой пакет. Я рисую гребни волн. В точке 1 произошла ионизация, и мы получили здесь каплю воды. Волновая функция скукожилась сразу в окрестности этой точки, но этот пакет обладает импульсом, он продолжает двигаться в том же направлении, эта волновая функция снова расплывается. Следующая конденсация произошла в точке 2, и так далее. На самом деле, толщина этого следа по атомным масштабам очень велика. Действительно, каждая капля, которая образуется (это измерение координаты электрона), ложится хаотично в пространстве, но все капли укладываются в след, толщина которого много больше длины волны. Они хаотически обнаруживаются в разных точках в пределах волнового пакета, ну а для нас это выглядит как такая траектория. Если бы мы были сами атомных масштабов и сидели там внутри, то мы видели бы, что он тут вспыхнул, потом он там вспыхнул, и никакой траектории мы тогда б не увидели. Таким образом вся эта картина увязывается со следами в камере Вильсона.

1)

Пока чисто математическая проблема.

При подстановке мы получаем уравнение: t равна некоторой функции от координат при любых значениях координат. Как это может быть? Только так, что обе эти функции константы. Это означает, что мы имеем два уравнения и в то же самое время

Сразу получаем, что удовлетворяет такому уравнению

                      (8)

И мораль такая: волновая функция Ψ вида

                                   (9)

удовлетворяет уравнению Шрёдингера, где функция удовлетворяет уравнению (8), которое называется уравнением Шрёдингера для стационарных состояний.

Это математический факт, какая физика за этим стоит? А физика такая – функция вида (9) описывает стационарное состояние частицы с энергией E. Стационарное означает, вообще-то, независящее от времени, а почему оно не зависит от времени, когда в (9) время явно сидит? Ещё раз напомню, сама волновая функция не имеет физического смысла, но физический смысл имеет квадрат её модуля, а и от времени не зависит.

Функция даёт распределение вероятностей обнаружить частицу в той или иной точке пространства, то есть она даёт пространственную конфигурацию этого состояния, и оно не зависит от времени. Мы имеем застывшую картину, а энергия этого состояния вполне определённая. Значит, есть энергия, но нет кинематики. Мы увидим дальше, что, например, электрон в атоме может находиться в стационарных состояниях с определённой энергией, а что касается пространственной зависимости вероятности обнаружить его в той или иной точке, то это застывшая картина. И, кстати, из этого мы можем понять, как будет решена проблема, которая возникает при применении классической механики к атому.

Как только обнаружилось, что в атоме есть ядро, то сразу родилась планетарная модель атома: положительное ядро и электроны, вращающиеся по орбитам, как планеты вокруг солнца. В эту модель сразу занеслось противоречие, потому что электроны, вращающиеся вокруг ядра, должны излучать электромагнитные волны за счёт своей энергии, – он очень быстро должен был бы свалиться на ядро.1) Мы сейчас видим, какова будет разгадка этой загадки.

Если электрон в атоме находится в стационарном состоянии, которое описывается функцией (9), то это застывшая картина, нет никакого движения заряда, со временем не меняется – нет излучения.

Вот таким образом решается проблема с электроном в атоме. Я ещё раз говорю, что этот образ электронов, вращающихся, как планеты вокруг солнца, вокруг ядра, который в классической физике присутствует, не имеет отношения к действительности.

Кстати, волновая функция описывает стационарное состояние (волновая функция для свободной частицы это частный случай стационарного состояния). Для плоской волны есть импульс, импульс это динамическая характеристика, а кинематики, то есть чего-то такого движущегося, нет, потому что вероятность всюду одинакова. Вот, когда мы возьмём волновой пакет, мы получим кинематику, но зато потеряем определённость в импульсе.

1)

Уравнение (8.2) нам даёт:

Слева от барьера было решение x,2) мы снова должны сшить эти функции в точке x₀=0.

Опять имеем четыре константы, и условия для сшивки (8.3) и (8.4). Константу C₁ мы считаем заданной (это мера интенсивности налетающего пучка), это отражённая волна, C₂ подлежит определению. В решении в правой части мы выкинем сразу, потому что функция экспоненциально нарастает, а это недопустимо для волновой функции (она интерпретируется как плотность вероятности): подлежит определению. Условие (8.3) даёт: 8.4):

        и        

Видно, что будет отлична от нуля:

То есть вероятность обнаружить частицу в классически запрещённой области отлична от нуля, – она экспоненциально затухает, но, все-таки, частица внедряется в эту запрещённую область. Частица уходит назад (интенсивность отражённого пучка такая же как интенсивность падающего, всё, что упало, всё отразилось), но то, что волновая функция не сразу обращается в ноль, физически проявляется в эффекте очень неожиданном на первый взгляд.

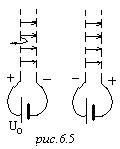
Туннельный эффект

Не будем решать эту задачу, она решается, но, просто, алгебра здесь длинная. Рассмотрим барьер конечной ширины – вот такую потенциальную энергию U(x) (рис.6.6, а).

Физически как реализовать эту ситуацию? Для электрона, поставив два конденсатора (рис.6.5). С точки зрения здравого смысла и классической механики что будет? Электрон летит, если его энергии достаточно, чтобы пробить конденсатор, то он через него пройдёт, долетит до следующего конденсатора, ускорится,вылетит и будет двигаться дальше с той же скоростью, с которой он подлетал. Если же у него энергии недостаточно, чтобы пробить первый конденсатор, то он сюда забурился, остановился, и его выбросило обратно, и он улетел, а что там дальше подставлять (человека поставить флажком махать или ещё что-нибудь) ему всё равно, он туда не долетает.

А вот в квантовой механике будет иначе. Качественно ситуация выглядит так.

За барьером мы получаем волну с той же длиной. Качественно довольно очевидно, ну а формально можно получить всё это, только в два раза больше сил потребуется, чем для ступеньки, поскольку больше граничных условий.

Это означает, что, если энергия частицы меньше высоты барьера, то существует тем не менее отличная от нуля вероятность, что она пролетит, то есть, когда вы ставите для электрона конденсатор с тормозящим полем, через него электрон заведомо не проходит, но если вы дальше поставите конденсатор с ускоряющим полем, то он пройдёт. Чем дальше будет второй конденсатор, тем больше ширина потенциального барьера, тем меньше вероятность.

Конечно, ситуация удивительная, чтобы её перевести на житейский язык, так скажем. Человек не прыгнет на 3м, чемпионы сейчас на 2.30 прыгают, но на 3м не прыгнут, даже я берусь спорить, что никогда не прыгнут.1) Теперь в чистом поле роем яму глубиной 3м и туда человека скинули. Он там может прыгать, но из ямы не выскочит. Другая ситуация: на ровном месте окружаем его стеной высотой 3м (барьер конечной ширины), тогда, если он будет прыгать достаточно долго и упорно, окажется, что он из ямы не выпрыгнет (ступенька потенциальная), а стену может преодолеть. Можно сказать, что нет вероятности выскочить из ямы глубиной 3м, но есть отличая от нуля вероятность перепрыгнуть трёхметровую стену.2)

Конечно, на макроскопическом уровне это (преодоление трёхметровой стены) выглядит как чудо, а в атомных масштабах это заурядная вещь. Вот использование электричества в быту связано радикальным образом с туннельным эффектом: всякий проводник покрыт тонкой непроводящей плёнкой, когда два проводника они разделены непроводящей плёнкой, электроны преодолевают эту плёнку за счёт туннельного эффекта.3) Вот так всё на благо человечества устроено.

Ещё один пример. Мы обсуждали фотоэффект. Электрон в металле сидит в потенциальной яме, и он не выскакивает, потому что имеет перед собой потенциальную ступеньку. А если мы за металлом убавим потенциальную энергию как на рис.6.7, а это можно сделать (см. рис.6.8), электрон в металле этого поля не чувствует, но он имеет перед собой барьер конечной ширины, а это означает, что имеется отличная от нуля вероятность, что он выскочит из металла. Это известный эффект, он называется эффектом В. Шотки, – если вы к куску металла приложите электрическое поле (оно всегда перпендикулярно к эквипотенциальной поверхности металла) такое, что для выскочившего электрона оно будет ускоряющим, то электроны начнут вылетать из металла.

1) Например, две частицы внутри вот этого куска мела находятся в связанном состоянии (они заперты в объёме этого куска), электроны в атоме так же находятся в связанном состоянии. Почему эти состояния важны? А вот потому, что энергия частицы в связанном состоянии может принимать лишь определённые значения 2) (энергия квантуется). Это очень существенное свойство, не имеющее, кстати, классического аналога. Земля вращается вокруг Солнца – строго говоря, её энергия квантуется, просто уровни энергии не заметны, в атомных масштабах заметны. По классическим представлениям энергия системы это определённое число, оно сохраняется, чем это число определяется? Начальными условиями, тем, как возникла эта система. Оно может быть любым, скажем, энергия могла быть чуть больше, чем она есть, чуть меньше, в классической механике это дело не регламентируется никак, всё определяется начальными условиями. А вот электрон в атоме может иметь какое-то значение E_n, которое можно заранее предсказать, и никаких других значений быть не может.3) Формально это проявляется так: уравнение Шрёдингера для стационарных связанных состояний имеет разумные решения лишь при определённых значениях E. Это факт математический, а его физическая интерпретация такая, что только эти значения энергии E могут наблюдаться. Мы сейчас убедимся на простом примере.

Частица в ящике

Мы сейчас смоделируем самое простое связанное состояние. Какое можно придумать самое простое связанное состояние? А вот такое – имеем ящик с абсолютно непробиваемыми стенками, с дверцей. Кинули туда частицу и дверцу захлопнули.1) Как это дело задать теперь математически? Потенциальная энергия в ящике равна нулю, вне ящика потенциальная энергия бесконечно велика, именно это и означает, что стенки ящика абсолютно непробиваемы (самый радикальный вариант связанного состояния). Дальше математика.

Мы рассматриваем стационарное состояние, волновая функция имеет вид: (пространственная часть волновой функции) должно выполняться уравнение

           Из того, что стенки ящика абсолютно непробиваемы следует, что частица вне ящика не может находиться, мы тогда пишем сразу вне ящика. А внутри ящика мы получим такое уравнение:

Это уравнение в частных производных. Будем искать решение в виде

то есть пытаемся разделить переменные.

Тогда

  

  

подставим это в уравнение:

Теперь делим всё это дело на XYZ, получаем тогда уравнение такое:

Первое слагаемое зависит только от x, а второе только от y, а третье только от z, и утверждается, что в сумме они равны константе. Тогда всё это дело разбивается на такие уравнения:

А это уже знакомые уравнения и мы немедленно находим решения:

Это решение в ящике, мы должны получить решение для всёго пространства, чтобы оно было непрерывным. Это означает, что волновая функция в ящике должна быть устроена так, чтобы она на стенках ящика занулялась. Это условие накладывает такие ограничения:

Займёмся иксом: даёт B₁=0, то есть константу B₁ мы выкинем сразу, даёт n_x=1, 2, 3… (значения A₁=0 и n_x=0 брать нельзя, потому что тогда мы убиваем всё решение). Таким образом, мы получаем такое условие: и u мы получаем множество решений такого вида:

                          (10)

При этом

И окончательно результат такой: состояние частицы в ящике задаётся тремя целыми числами, которым соответствует функция (10), и этому состоянию соответствует энергия a, b, cэто рёбра ящика. Вот что такое квантование, имеем дискретные состояния (тройка чисел задаёт волновую функцию определённой конфигурации) и этим состояниям соответствует энергия. Важно, что нет никаких промежуточных состояний, переходных форм нет. Состояние (1,1,1) называется основным, оно имеет минимальную энергию, а максимальная вероятность найти частицу в ящике [для этого состояния] – в середине, то есть вот частица большую часть времени проводит в середине ящика вместо того, чтобы бегать от стенки к стенке.

8

Продолжаем ту же тему. Если ящик кубический, то формулка для энергии делается симпатичнее:

Возможны различные состояния, которым отвечает одна и та же энергия. Состояниям (2,1,1), (1,2,1), (1,1,2) отвечают различные волновые функции, то есть вероятности обнаружения частицы в точках ящика разные в этих состояниях, но понятно, что им отвечает одна и та же энергия. Уровень энергии, которому отвечают несколько различных состояний, называется вырожденным, в частности, уровень, отвечающий этим трём состояниям, называется трёхкратно вырожденным.

§6 Постулаты квантовой механики

1. Векторы и операторы

2. Постулаты квантовой механики

3. Операторы динамических переменных. Координатное представление

4. Оператор энергии

5. Оператор импульса

6. Момент импульса (собственные векторы, собственные значения)

7. Спин.

Мы с вами обсудили некоторые аспекты физики систем атомных масштабов, волновые свойства частиц, квантование энергии, туннельный эффект… Это всё были отдельные фрагменты, не связанные более-менее друг с другом, это ситуация на заре создания теории, когда обнаружилась длина волны де Бройля, интерференция. И многого мы вообще не знаем, например, знаем волновую функцию, а что мы получим при измерении импульса? Мы ещё не умеем отвечать на такие вопросы. Сейчас мы обсудим как устроена окончательная теория.

От первой модели атома Бора и до окончательной формулировки теории прошло 10-12 лет,1)  и мы сейчас обсудим, как вообще строится вся эта теория.

Если сравнивать с классической механикой, раз нет траектории, скоростей, ускорений, сил, то понятно, что математическая структура должна быть другой.2) Можете сейчас забыть про классическую механику, можете даже забыть то, что мы до сих пор тут обсуждали, и сейчас мы снова будем смотреть незамутнённым взглядом на новую теорию. И тут нужны некоторыематематические подмостки.

3)

Удобство этих обозначений состоит вот в следующем: – это число, скалярное произведение двух векторов: – скалярное произведение вектора на сопряжённый ему вектор, это будет действительное число,

Такое равенство расшифровывается так: есть правило, которое вектору ставит в соответствие вектор действует некоторый оператор, в результате действия которого, мы получаем вектор

Если имеет место такое равенство 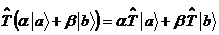линейным.1) Дальше, когда идёт речь об операторах, имеются в виду только линейные операторы.

Каким образом можно задать это правило, то есть как можно задать оператор? Если оператор линейный, то вот такой строчкой: . Задайте квадратную таблицу , любых чисел навтыкайте туда, эта матрица представляет линейный оператор.

Любая матрица представляет некоторый оператор

Если матрица оператора получается из элементов матрицы оператора с помощью транспонирования и комплексного сопряжения элементов: называется эрмитово сопряжённым к оператору

Если называется самосопряжённым или эрмитовым.1)

Если α – число, то вектор называется собственным вектором оператора α – собственным значением, отвечающим этому собственному вектору.2)

Оказывается, что эрмитов оператор n собственных векторов, которые будем обозначать и собственные векторы эрмитова оператора ортогональны, а соответствующие им собственные значения действительны. Это наш реквизит, это факты математические, а теперь возвращаемся к физике.

3) предполагается, что

Утверждение 2. Каждой наблюдаемой динамической переменной A (координаты, импульс, момент импульса …) ставится в соответствие эрмитов оператор

Вектор переменной в абстрактном пространстве изображается столбцом, оператор, отвечающий этой переменной, в этом же пространстве будет изображаться квадратной матрицей. Кстати, эпитет «наблюдаемый» не для красного словца. Наблюдаемая переменная – это переменная, которую можно измерить.1)

Утверждение 3. При измерении динамической переменной A(вот я подставляюсь под пулю, ловлю её и мерею её импульс) могут быть получены числа лишь из ряда собственных значений соответствующего ей оператора

Сейчас мы это дело оформим более компактно. Если Aможет быть получено одно из чисел α₁, α₂, …, α_n.

Утверждение 4. Вероятность того, что при измерении переменной A частицы в состоянии, задаваемом вектором α_n равна:

Третий постулат утверждает, что при измерении переменной A могут получаться лишь числа α₁, α₂, …, α_n, какое из них получится при конкретном измерении, теория отказывается отвечать, но она говорит, что вероятность того, что будет получено значение α_k, например α₇, будет определяться по такому рецепту.  Возьмите вектор состояния частицы, умножьте скалярно на собственный вектор, отвечающий этому собственному значению, получится комплексное число, найдите квадрат модуля этого числа, и вы получите вероятность того, что будет получено значение α₇. Этот рецепт можно выразить в более доступной форме.

Векторы по базису из собственных векторов оператора (квадрат модуля проекции вектора на собственный вектор оператора) даст вероятность того, что при измерении переменной A будет получено значение (соответствующее собственное значение).

Утверждение 5. Существует эрмитов оператор (гамильтониан) такой, что имеет место уравнение

уравнение Шрёдингера.

Короче говоря, существует оператор, который заведует изменением вектора состояния со временем. Малое изменение вектора за время будет равняться: в данный момент оператором , разделим на 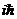вращается, вот этот маленький поворот определяется оператором

Ну, что тут пока неудобно? Всё это звучит, наверное, замечательно и захватывающе, только не понятно, зачем это делали. В ньютоновской механике, когда всё там написали (Второй закон ньютона, силы), поскольку много лет все слышали, это кажется очевидным, а ведь на самом деле это голая форма, никакого содержания она не имеет. Содержание появляется только тогда, когда даются рецепты, что там в правой части писать. Ньютоновская механика это, на самом деле, утверждение такого сорта, что всё многообразие мира мы можем отлить в форму дифференциальных уравнений второго порядка, подбирая соответствующие функции в правой части. Именно на этом стояла физика фактически до конца XIX века, считалось, что всё, что мы тут видим, оно вот в эту простую математическую форму отольётся, если мы только правильно подберём эти функции, и зада физики тогда была придумать эти функции в правой части, чтобы отлить в эту форму. На самом деле мир оказался хитрее, и он не отливается в теорию дифференциальных уравнений второго порядка. Здесь мы пока тоже видим математическую форму. Утверждается, что мы подберём операторы такие, что всё окружающее нас тут отольём в эту математическую форму. В ньютоновской теории задача физики была в нахождении сил, в рамках этой механики задача физики это нахождение гамильтонианов, то есть операторов, которые определяют эволюцию состояния в заданной окружающей среде, а окружающая среда характеризуется гамильтонианом. Вот такая математическая структура.

1)  Если взяты собственные векторы оператора говорят, что мы работаем в A-представлении. Тогда все векторы и все операторы будут выражаться в этом базисе. Если – оператор координаты, тогда имеет место такое равенство: – собственный вектор, отвечающий собственному значению q. Если в качестве базисных векторов будут взяты векторы координатном представлении.

9

Проблема такая: как связать абстрактное пространство, в котором разыгрываются все эти события, с нашим реальным наблюдаемым миром, в котором мы живём? Как нам отсюда пролезть туда, в этот потусторонний мир, в котором действуют правила игры, которые мы сформулировали. Лазейка такая: чтобы задать вектор в виде набора чисел, надо предъявить базис. Операторы, с которыми мы имеем дело (это эрмитовы операторы), обладают тем свойством, что для них имеется n собственных векторов, эти собственные векторы эрмитова оператора ортогональны, если в качестве базиса выбрать собственные векторы оператора, то его матрица в этом базисе будет диагональной, а по диагонали будут стоять собственные значения.Собственные значения – это те числа, которые мы получаем при измерении переменной, которую описывает данный оператор. Вот так можно состыковать эти абстрактные математические объекты с реальными наблюдаемыми величинами. Если мы, например, экспериментально исследовали набор собственных значений данного оператора, то мы сразу можем написать его матрицу в базисе его собственных векторов, просто по диагонали расположивши эти собственные значения. Есть законы, которые связывают операторы друг с другом, и если мы нашли один оператор, то просто зная связь между этими операторами, мы можем построить и другие операторы. Мы тогда получим матрицы в том представлении, в котором исходный оператор был диагональным.

Если это оператор координаты, а – собственный вектор этого оператора, отвечающий собственному значению q, то есть имеет место такое соотношение: 1) оператор действует на собственный вектор, получается тот же собственный вектор, которому отвечает число q.2)

Произведение операторов

Если действует на некоторый вектор (на любой), это то же самое, что 3) Матрица оператора представится, оказывается, как произведение матриц Bи A, то есть

Произведение операторов, вообще говоря, не коммутативно (потому что произведение матриц не коммутативно), то есть когда мы действуем оператором или наоборот, сначала 4) Разность произведений это некоторый оператор: и называется коммутатором операторов и

Переменные, операторы которых не коммутируют (коммутируют), не могут (могут) быть измерены [и заданы] одновременно.

Мы уже сталкивались с такими вещами. Иксовая координата частицы и иксовая компонента импульса xи не могут быть заданы одновременно: нельзя сказать, что частица имеет точно такую координату и имеет такую-то составляющую импульса, есть соотношение неопределённости. Это, кстати, означает, что операторы и не коммутируют.

Утверждение. Постулируется, что .1)

Но, кстати, например , это означает, что одновременно мы можем задать координату и игрековую составляющую импульса (или зетовую), а вот иксовую задать не можем, и измерить одновременно не можем. Это можно написать в более общем виде: .

Из того, что , следует, что спектр собственных значений оператора координаты непрерывен. Иначе говоря, мы можем задать любое число q, и для него найдётся вектор . Физически это означает, что при измерении координат может быть получено любое число или, ещё проще говоря, координаты не квантуются.2)

Существует координатное представление, когда в качестве базисных векторов выбираются собственные векторы оператора координаты. Произвольный вектор может быть выражен в этом базисе. Если бы эти собственные векторы нумеровались каким-то дискретным параметром 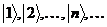представился бы суммой

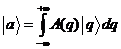
функция это функция, удовлетворяющая двум условиям:

1)

2)

В координатном представлении вектор состояния изобразится интегралом: – это коэффициенты разложения вектора по базису из собственных векторов оператора координаты, это то, что у нас называлось волновой функцией. Вот таким образом стыкуется то, что раньше говорилось о волновой функции, и её представление в абстрактном пространстве.

Раньше я говорил, что волновая функция описывает состояние частицы с импульсом и с энергией выражен через базисные векторы, которые мы обозначаем 1)

А как быть с другими операторами? Пусть у нас для простоты на этот вектор 2) =подействовал на вектор x. Таким образом, в координатном представлении действие оператора на функцию сводится просто к умножению этой функции на число, то есть мы можем написать, что в координатном представлении

Как же импульс? Оператор действует на вектор

3)=

Таким образом, в координатном представлении действие оператора на функцию приводит к взятию частной производной и умножению её на число

И, наконец, последнее. Если мы имеем какую-то функцию координаты и импульса будет та же самая функция, но взятая от операторов и

10

Ещё раз, как можно ткнуть пальцем и предъявить базисные векторы, если мы работаем в абстрактном пространстве? В качестве базиса выбираются собственные векторы какого-нибудь оператора. В таком базисе этот оператор выражается диагональной матрицей, где по диагонали стоят собственные значения, а собственные значения – это наблюдаемые величины, поэтому, если мы экспериментально определяем собственные значения оператора, то мы его матрицу тут же пишем. Операторы связаны между собой (по теории), тогда другие операторы можно находить через матрицу, которую мы нашли. Это общая программа. Теперь конкретное исполнение.

Рассматривалось специальное представление – в качестве базиса были выбраны собственные векторы оператора координаты (тогда собственные значения этого оператора это просто координаты частицы, которые мы экспериментально можем определять). Из постулируемого коммутационного соотношения можно доказать, что собственные значения оператора координаты непрерывны. Оказывается, что в этом базисе оператор принимает вид задаёт компоненты вектора в координатном базисе, то функция задаст компоненты вектора в том же самом базисе, так как .

Мы уже получили два оператора, оператор координаты и оператор импульса. Как быть с остальными? Лекция была кончена утверждением, что если некоторая переменная A есть функция координаты и импульса будет функция от операторов и 1)

А вот если переменная не имеет классического аналога, а в квантовой механике появились такие переменные (например, спин), вот там приходится оператор для переменной изобретать.

1)

Собственные значения нумеруются вектором или в координатном представлении с таким собственным значением: любой.

1)

В координатном представлении оператор импульса есть: задаётся некоторой функцией и должен изобразиться так: 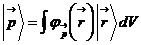или это функция от x только, то можно писать прямую производную:

Решение находится сразу:

Это собственная функция оператора импульса, отвечающая собственному значению

Утверждение. Функция является решением этого уравнения.

Доказательство. Подставляя эту функцию в уравнение, мы получаем:

Функция является собственной функцией оператора импульса, соответствующей собственному значению

Отсюда видно, что собственным значением оператора импульса может быть любой вектор.

Если операторы двух переменных коммутируют, то эти переменные могут быть заданы и измерены одновременно, а операторы имеют одинаковые собственные векторы, ну и поэтому собственные значения могут быть заданы одновременно. То, что нельзя одновременно задавать координату и импульс, мы обсуждали, можно ли одновременно задать координату и энергию? Ответ зависит от того, коммутируют или нет операторы координаты и энергии. Ответ такой: оператор энергии со вторым слагаемым прокоммутирует, а с первым нет (это следует из коммутационного соотношения). Это означает, что координату и энергию задать вместе нельзя никогда, то есть не может быть утверждений, что частица находится в некоторой точке пространства и имеет такую-то полную энергию (они не коммутируют). Другой вопрос: импульс и энергию задать можно или нет? Вроде бы ответ напрашивается, что в коммутационное соотношение координата и импульс входят симметрично, но оператор энергии координата и импульс входят несимметрично, является одновременно собственной функцией оператора импульса и энергии, собственные значения связаны так:

11

Мы нашли, что 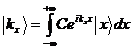1)Векторы могут быть выбраны сами в качестве базиса, в котором можно выражать все другие векторы, это называется импульсное представление.

Чтобы покончить совсем с оператором импульса и собственными значениями оператора импульса, окончательно оформим это так: оператор действуя на вектор даст: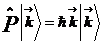собственные значения оператора будут равняться изобразится так:

1) Собственные векторы и собственные значения будем нумеровать двумя числами – два числа jи m определяют вектор и (это возможно, потому что эти операторы коммутируют и у них общие собственные векторы).

При этом

Ситуация такая: задаёте jиз набора (j, m) определяет вектор в абстрактном пространстве, который мы обозначаем вот с такими собственными значениями: с собственными значениями

Мораль такая: квадрат момента квантуется и может принимать лишь значения z может принимать значения кратные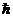

Оказалось, что если j принимает целые значения

1) Пусть создаётся такое магнитное поле (см. рис.7.1). Теперь мы сюда запускаем пучок частиц, обладающих магнитными моментами. Когда частица залетает в магнитное поле, на неё действует сила по вертикали 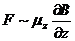2) Тогда, если влетает пучок частиц с хаотично ориентированными магнитными моментами, то на каждую из этих частиц будет действовать сила пропорциональная направлению магнитного момента на ось z. Каждая частица будет отклоняться пропорционально силе, т.е.

Это способ определить экспериментально проекцию магнитного момента, которая связана с орбитальным моментом:

А теперь мы запускаем туда не макроскопические элементы, а запускаем пучок атомов, а атом тоже может обладать магнитным моментом за счёт того, что там электрон вращается. А когда мы пропускаем пучок атомов, то обнаруживается, что мы не получаем такого размазывания в виде веера этих траекторий, а будет наблюдаться такое (скажем, пучок может разделиться на три пучка):

Пучок атомов не размазывается, они расщепятся, а именно три чётких отдельных пучка появится. Как это проинтерпретируется? Это будет означать, что проекция магнитного момента на ось z принимает всего три значения, а число проекций 2j+1 = 3 и j = 1, мы тогда говорим так: эти атомы обладают орбитальным моментом определённое число пучков. Вот, целым j отвечают такие орбитальные моменты. Но оказалось, что есть ситуации, в которых пучок расщепляется на два пучка (рис.7.2. б). Это означает, что 2j+1 = 2 и . Эта ситуация, как выяснилось в конце концов, связана с тем, что электрон обладает собственным магнитным моментом, т.е. полуцелым значениям j не отвечают орбитальные моменты, значению отвечает собственный момент импульса электрона и он называется спином.

Ситуация выглядит так, что электрону, точечному объекту, приписывается собственный момент импульса, ему же отвечает соответствующий момент, и собственный магнитный момент электрона 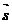такой, что

8. Средние значения динамических переменных

Мы уже видели, что теория отказывается предсказывать, что мы получим в результате измерения той или иной величины, она предсказывает лишь вероятности того, что будет получено то или иное значение. В связи вот с этим вероятностным характером возникает вопрос, каково среднее значение переменной? Ответ на это простой. Пусть мы имеет какую-то переменную A, и этой переменной соответствует оператор A в состоянии (угловыми скобками будем обозначать) будет определяться так:

Откуда берётся такой результат? Пусть – собственные векторы оператора a_n – соответствующие собственные значения. Векторможно представить в виде разложения по собственным векторам оператора

=

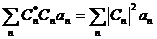
а 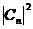– это вероятность получить при измерении переменной A в состоянии значение a_n. Возможные значения умножаются на вероятность и суммируются по всем возможным значениям, а это то, что в математике называется математическое ожидание, это и есть среднее значение данной величины.

---

1) Вот, я слышал, математик известный придумал, что все эти временные шкалы ерунда, и вообще, мир начался где-то 300 лет назад что ли, а всё остальное – подделки, фальшивки и подтасовка фактов. Бред собачий. Тут даже не о чем говорить. Дело в том, что имеются разные временные шкалы: хроники, углеродный способ датировки и прочее – это вещи не из одного источника, это всё согласовано. Я не знаю, что должно произойти в голове, чтобы вот так зациклиться на такой бредовой идее.

2) Нет до сих пор надёжной модели, представления о возникновении солнечной системы, но, во всяком случае, как бы она там не возникла, все характеристики, которые она имела бы, это по отношению ко всему дальнейшему случайные начальные условия. Земля могла бы быть ближе к Солнцу, могла бы быть дальше, параметры орбит были бы другими. Ну, например, более-менее понятно, почему орбиты всех планет лежат приблизительно в одной плоскости, скажем, из вращающегося диска это могло образоваться, опять же это начальные условия.

1) На самом деле, там не этот аспект взаимодействия правильный, то есть классическая теория и здесь оказалась неверной. На счёт рассеяния (с синевой неба) она сработала, но по причинам, которые мы дальше увидим.

1) Если мы видим воду – это просто, ещё не успевшая испариться, вода.

1) Наглядная картина: вырыли в земле яму глубиной 3м и кинули туда узника. Высота барьера, потенциальная энергия, h = 2м. И вот он там в этой яме прыгает, и всё, – прыгает, прыгает, а ему ещё не хватает куска в 1м. Так из этой ямы ему не выбраться никогда.

2) Не то, что есть явления, к которым неизвестно как подступиться, любому человеку можно предложить задачу, которую он не знает, как решить, это ещё не дефект науки, это сложность задачи и дефект того, кто её пытается решить. Здесь другая ситуация: проблема ясная, как её решать тоже понятно, действуем по правилам, – получаем ерунду (не то, что мы не знаем, как её решать). Это дефект теории, а не того, кто её применил.

3) Во времена Ньютона уже была гипотеза о том, что свет это есть волна, Гюйгенс в частности был её последователем, и другая, что свет есть поток частиц, то есть светящееся тело испускает какие-то частицы. В те времена нельзя было их проверить. Можно было говорить, как Гюйгенс, что это есть волны, и объяснить наблюдаемые явления, то, что называется геометрической оптикой. Преломление света и отражение одинаково хорошо и та и другая теория объясняла. Вот, когда было обнаружено явление интерференции (опыт Юнга в начале XIX века), тогда восторжествовала волновая теория. И для объяснения взаимодействия света с веществом пришлось вернуться к корпускулярным представлениям.

1) Какая масса, покоя или релятивистская, стоит в формулах? – вопрос из зала. Масса, которая стоит в этой формуле это свойство частицы. Вот у вас есть килограммовая гиря, на ней написано «1кг», как бы эта гиря тут не летала, надпись «1кг» сохраняется. Это отголоски того, что в своё время любили различать массу покоя и полную релятивистскую массу, которая вроде бы зависит от скорости. Здесь, когда я пишу m, это свойство частицы (в таблице смотрим).

2) Это не означает, что нет смысла убегать. Например, гонится за вами фотон, вы от него бежите со скоростью c, но есть смысл убегать, потому что меняется не его скорость, а меняется его импульс. Если вы будете быстро убегать, то импульс, с которым он вонзится вам в спину, будет гораздо меньше (и может быть сколь угодно малым), он вас настигнет так же быстро, как если бы вы стояли на месте, но эффект будет не тот.

1) Потому что, если бы, например, по понедельникам он вёл себя как волна, а по вторникам как частица, это была бы проблема, конечно, это бы подорвало основы науки.

2) Я даже не буду говорить тут «свет», - «объект».

3) При этом фотон должен поглотится электроном с самой большой энергией, иещё должно оказаться так, что импульс электрона направлен наружу.

4) Дальше идут два вопроса из зала.

1) Когда сталкиваются два бильярдных шара, исход столкновения на основе законов сохранения энергии и импульса описать нельзя (иначе не было бы игры в бильярд), он ещё зависит от так называемого прицельного параметра.

1) Не на свете (для света в видимой области условие сохраняется), а наблюдалось рассеивание рентгеновских лучей на электронах, то есть на обычном атомном веществе (электрон в атоме хотя и связан, но энергия этой связи по сравнению с энергией рентгеновского фотона мала).

1) Можете поупражняться и посчитать, сколько света сваливается на Землю, если считать, что Солнце излучает изотропно.

2) Легко понять, почему заряд, движущийся с ускорением, должен излучать. Вот у вас неподвижная заряженная частица, к ней приклеено кулоновское поле, силовые линии которого расходятся до бесконечности. Начинаем дёргать заряд, понятно, что вместе с ним дёргаться это поле не может (когда я его тут сдвигаю, в удалённой точке поле не может «знать», что я его тут сдвинул), ближайшее поле сдвинулось, а на большом расстоянии поле стоит. Это означает, что происходит отрыв поля от заряда, а поле, оторвавшееся от заряда, это уже свободное электромагнитное поле, которое может находиться лишь в определённом состоянии: векторы и перпендикулярны, модули их согласованы и всё это плывёт со скоростью света.

1) Излучение не может происходить с одинаковой мощностью на всех длинах волн, в этом случае энергия была бы бесконечно велика.

2) Это привычное название, и другое, более-менее старорежимное, монохроматическая испускательная способность.

3) Механизм отражения мы рассматривали – это вторичное излучение атомов предмета.

4) Когда-то рассказ я читал, по-моему, у Джека Лондона как там были два соперника (о чём они соперничали, я уже не помню, хотя у них там сюжет всегда одинаковый), и один из них стал абсолютно чёрным, а другой стал абсолютно прозрачным. Ну, игра там какая-то была, что тот, который был абсолютно прозрачный, тоже был вроде бы невидимым, но иногда как-то бликовал на солнечном свете, а абсолютно чёрный якобы был вообще невидим. Кстати, человек-невидимка не мог бы функционировать, если бы он был бесцветным! Если бы он был действительно невидим, это означает, что он никак не взаимодействовал бы с излучением, излучение проходило бы насквозь, не взаимодействуя с ним, он бы тогда ничего и не видел (потому что мы видим за счёт того, что сетчатка глаза там как-то взаимодействует с излучением). Так что мало того, что его никто не видел бы, но и он бы никого не видел, ну, и радости, конечно, от этого не было бы никакой.

1) Нейтрино пронизывают Землю без всяких потерь, без всякого взаимодействия, это частицы, которые предельно слабо взаимодействуют с веществом, то есть какой-нибудь слой свинца толщиной от Земли до Солнца лишь в ничтожнейшей степени ослабил бы поток нейтрино. Солнце излучает мощные потоки нейтрино, частицы, сопровождающие ядерные реакции, и они нас просвечивают запросто на теневой стороне Земли и на световой стороне.

2) Напомню, эта дыра представляет собой сферическую поверхность (хотя бывают вращающиеся дыры, и поверхность не сферическая) в пространстве, куда всё валится внутрь и ничего обратно не вылетает. Недавно, кстати, слыхал, что обнаружили объект, который тянет на чёрную дыру (уже известно 20 таких объектов) массой порядка 107 солнечных масс, большая дыра. Кстати, как массу этой дыры понимать? Она создаёт гравитационное поле, вот по полю на бесконечности с помощью закона тяготения (Ньютона) определяется масса.

3) Мы сейчас с вами сидим в такой полости, так что это не какая-то хитрая вещь, мы большую часть жизни проводим в таких полостях. Только нужно было бы выключить лампы и нас отсюда вывести, потому что наша температура выше.

1) Отполируем поверхность, она будет меньше поглощать, скажем, полированный стол больше отражает, чем какая-то неполированная деревяшка.

2) Вот у вас кусок железа излучает при данной температуре, отполируйте его поверхность, его излучение изменится!

1) Если вы откроете дверцу только что протопленной печки, то увидите излучение чёрного тела. Космическое пространство всё в масштабах Вселенной заполнено равновесным электромагнитным излучением с температурой 3⁰K, то есть с таким, с каким было бы излучение в полости с температурой стенок 3⁰K, это так называемое реликтовое излучение, оставшееся со времён возникновения Вселенной. Если расширение будет продолжаться, температура будет падать и дальше, в конце концов до абсолютного нуля, если расширение сменится сжатием, температура будет возрастать, и весё вернётся к начальному состоянию с большими температурами.

2) Классическая физика не смогла получить разумную формулу для спектральной плотности (эта формула легко проверяется: абсолютно чёрное тело – печь, ставят спектрометр, излучение в спектр разворачивается, и для каждой полоски спектра можно найти энергию в этом интервале длин волн). Классическая физика не смогла не только дать правильное значение функции, она не смогла дать даже разумное значение, а именно, получалось, что эта функция растёт с убыванием длины волны, а это просто бессмысленно, это означает, что любое тело в видимой области излучает, а в низких частотах ещё больше, и полная энергия излучения стремится к бесконечности. Значит, в классической физике есть какие-то принципиальные дефекты.

3) Факт хорошо известный: вы можете сунуть горячий утюг в печку, изначально он будет тёмно-красного цвета, если его греть дальше, цвет будет желтеть (по мере роста температуры это дело начинает выезжать в видимую область), ну и, наконец, станет белым. Что называют белым светом? Солнце светит, как абсолютно чёрное тело, значит, спектральный состав солнечного излучения это по определению белый свет.

4) Обычные лампы накаливания это пример теплового излучения. Температура нити в лампе чуть больше 2000 градусов, можете легко посчитать на какую длину волны приходится максимум, оказывается, в инфракрасной области, то есть лампа работает неэффективно, в видимой области её излучение это несколько процентов от потребляемой мощности, в основном она действует на обогрев.

1) Это означает, что, если нет частицы, движущейся по траектории, то нет скорости, нет ускорения, не к чему применять Второй закон Ньютона, и, вообще, вся эта схема классической механики не работает.

2) Соорудить поток электронов вполне возможно: в телевизионной трубке, в электронной пушке, электроны излучаются из раскалённой нити, ускоряются электрическим полем, луч формируется, и на экране рисует картину.

3) Вместо пучка электронов можно представить поток пуль из пулемёта, щит броневой со щелью, а дальше деревянный забор регистрирует попадания пуль, понятно, что они будут рассеиваться, проходя через эту щель.

1) На рис.1.c точка отмечена крестиком

1) Так сказать, пока частица не обнаружилась где-то, Господь Бог, понимая под этим существо, которое знает всё, что можно знать, он не знает, где она будет обнаружена,он тоже может оперировать только вероятностью. В рамках этой же метафоры Господь Бог-то знает, где молекулы воздуха летают, это мы не знаем, но он знает, потому что, в принципе, можно за ними следить и можно знать, где какая из них. А где будет обнаружена частица, описываемая волновой функцией, это и Господь Бог не знает. Вот такая ситуация. Разные аспекты этого дела ещё проявятся более занимательным образом.

2) Это довольно тонкая вещь. Язык это наше произведение, он развился в процессе общения, всё ли существующее в мире можно сформулировать на языке? Могут быть вещи, которым у нас, вообще, и слов нет, мы о них не можем задуматься, но это другая проблема. Но то, в квантовой механике обнаружилось, в общем, это очень сильно повлияло в общефилософском плане на наше представление о том, какие высказывания разумны, а какие высказывания бессмысленны.

1) Почему мы считаем, что уравнения Максвелла справедливы? Потому что работает теория: радиоприёмники говорят, телевизоры картинку показывают, и, вообще, всё, что называется электричеством, железно из этих уравнений следует.

1) В чём состоит функционирование физика? Он должен уметь слова обычного языка переводить в какие-то математические формулы, вот и всё. Допустим, человек обычным языком описывает проблему, а специалист должен будет потом, зная законы природы, сказать, что будет. Так вот, специалист должен будет перевести эту, может быть, и несвязанную речь на язык математики. На этом функция физика кончается, потому что, как только он перевёл, он может пойти к знакомому математику и дать ему математическую проблему и сказать, вот решай. Математик его не будет спрашивать, что такое буква Ψ, буква t, математику важно знать, что это некоторая функция от переменных x, y, z,ему не надо знать, что эти переменные представляют. Математик это всё продолбит и даст решение, не понимая, что всё это означает. Дальше, опять физик может это проинтерпретировать. Значит, физик работает только на стадии перевода. Но такого разделения труда между физиками и математиками нет, и физикам всегда приходится работать по совместительству математиками, более того, математика в XVIII, XIX веке развивалась в основном физиками, потому что проблемы брались из физики. Вклад чистых математиков в эту науку оказался удивительным, и при случае, если не забуду, я об этом поговорю.

2) Чем замечательны экспоненты – их дифференцировать приятно.

3) Есть рецепт дивергенции от произведения скалярной функции на вектор:

1) Луи де Бройль, кстати, недавно умер, хотя это придумал в 20-х годах. Он из королевской семьи, это один из последних Бурбонов.

1) В классической физике тоже понималось, что, когда мы наблюдаем объект, то мы с ним взаимодействуем: надо объект осветить и смотреть, по крайней мере, отражённый свет. Но в классической физике считалось, что это взаимодействие можно сделать настолько малым, что оно не меняет состояния объекта, но это оказалось большим заблуждением: в области атомных масштабов наблюдение нельзя сделать таким, чтобы оно не меняло состояния объекта. Наблюдение само по себе это вовсе не невинное дело: когда мы взаимодействуем с объектом в атомных масштабах, его состояние меняется.

2) Мы обсуждали в своё время разрешающую способность оптических инструментов, к сожалению, на экзамене я убедился, что многие эту вещь проигнорировали. Совершенно дифракционное явление: в микроскоп мы можем разрешить две близкие точки, то есть воспринять их как две различные точки, если расстояние между ними не меньше длины волны. Длина волны света, который используется в микроскопе, определяет разрешающую способность.

1) Любая реальная волна, согласно теореме Фурье, может быть представлена как суперпозиция монохроматических волн с различными амплитудами и частотами ω в некотором интервале Δω. Суперпозицию волн, мало отличающихся друг от друга по частотам волновым пакетом или группой волн. //И.Е. Иродов. Волновые процессы. М.1999. стр. 223.

2) Простейший наглядный пример – звуковая волна. Кто-нибудь издаст сейчас кратковременный вопль, и побежит звуковая волна длиной τ – длительность вопля. Кстати, если длительность вопля полсекунды, то длина этого пакета будет 150м. И побежит такое возмущение длиной 150м, оно, конечно, не монохроматическое, там уже появится целый спектр частот, и чем кратковременнее вопль, тем больший набор частот требуется для этого.

¹) Поясним эту формулу на примере суперпозиции двух волн с одинаковой амплитудой и несколько отличными друг от друга длинами волн (и частотами). На рис.3.2, а показано их относительное расположение в некоторый момент времени, а на рис.3.2, б – результат их суперпозиции. Нас будет интересовать скорость, с которой перемещается место с максимальной амплитудой – это и будет скорость волнового пакета – групповая скорость.

//И.Е. Иродов. Волновые процессы. М.1999. стр.224.

1) Наглядный пример. Приходилось, наверное, наблюдать забеги на длинные дистанции. Вот группа бегунов стартует, эта компактная куча начинает бежать. Отдельный бегун – это отдельная синусоидальная составляющая. Потом, поскольку бегуны все разные, бегут с разными скоростями, это начинает размазываться: сначала бегут компактной группой, потом эта группа разбивается, потом, вообще, оказывается, один на круг отстаёт, и всё начинает путаться. Вот расплывание пакета.

2) Теперь понятно, почему существует классическая механика, почему она оказалась правильной. Например, масса пули m=10^-2,допустим центр масс пули был локализован в интервале Δx₀=10^-5м. На сколько увеличится неопределённость в координате пули за какое-то время? Δx~10^-27t. За сутки полёта пули (t=10^-5) мы получим Δx~10^-22. 10^-10 – размер атома водорода. Потому-то пули и летают как компактные объекты, потому что у них масса достаточная, потому и справедлива классическая механика. Если мы в формулу подставим массу электрона m_e~10^-30, томы видим, что для электрона волновой пакет мгновенно расплывается, и его координата сразу теряется через относительно короткое время.

1) Можно жидкость, например, нагреть в обычных условиях до температуры выше 100^о, и она не будит кипеть, если греть очень чистую жидкость без всяких примесей, греть осторожно. Кстати, если потом эту кастрюлю с такой жидкостью немножко тряхнуть, она взрывается, она мгновенно испаряется. Точно так же можно аккуратно охлаждать водяной пар в чистом воздухе до состояния с температурами ниже той, при которой он должен был бы сконденсироваться и превратиться в воду и даже в лёд.

1) Понятно, что вовсе не всякая функция представляется в таком виде, скажем, не всякая функция f(x, y) представляется в виде g(x)h(y), поэтому, если мы найдём такие решения, то это будут какие-то специальные решения.

1) Немедленно вопрос может возникнуть, почему планеты вращаются вокруг Солнца? Мы детально не обсуждали, как выглядит настоящая полевая теория для гравитационного поля, но, когда Земля вращается вокруг Солнца, то поле должно меняться синхронно, а поскольку синхронно меняться не может, то должны излучаться гравитационные волны. Почему тогда Земля не падает на Солнце? Ответ простой – мощность мала. Волны излучается, энергия уносится, но гравитационное взаимодействие примерно на 40 порядков слабее электромагнитного, это самое слабое взаимодействие. Энергия уносимая волнами просто очень мала, и, скажем, Земля за 4 млрд. лет, сколько она существует, сделала 4 млрд. оборотов, но приблизилась к Солнцу ничтожно мало.

1) Если кинетическая энергия электрона меньше, чем работа по преодолению тормозящего поля, то налетающий электрон внутри останавливается и выбрасывается обратно. Это по здравым представлениям, ну, и по классической физике. Посмотрим, что даёт наша теория.

2) Непрерывность гарантирует, что вероятность не прыгает резко при малом смещении, то есть вероятность меняется непрерывно.

1) Вот, кстати, на счёт предела в рекордах. Вы, наверное, анализ изучали, там сказано, что всякая монотонная ограниченная последовательность имеет предел. Когда я был на вашем месте, как только услыхал такую теорему, меня пронзило – это означает, что любые рекорды имеют предел. Рост рекордов в прыжках, в беге это заведомо ограниченная последовательность, стало быть, есть предел, то есть когда-то все эти спортивные соревнования упрутся в смысле рекордов.Конечно, прыгать можно всегда, потому что это личные соревнования, но рекорды расти перестанут. Такая вот эта теорема.

2) Если бы человек выскочил из ямы, так сказать, прыгнул выше головы, то нарушился бы закон сохранения энергии (у него нет энергии, чтобы подскочить на 3м). Но если он оказывается за стеной, его энергия в начальном состоянии и в конечном одна и та же, просто произошло действие, несколько запрещённое с точки зрения классической физики, но нарушения закона сохранения энергии нет.

3) Если бы не было туннельного эффекта, то с электричеством было бы не так просто. Это означает, что вы должны были бы, например, провода, ведущие к вашему чайнику, впаять в него, а другие два конца привести на электростанцию и впаять туда, чтобы было сплошное металлическое тело. Просто при механическом контакте ток не потёк бы, если б не было туннельного эффекта.

1) Земля, движущаяся вокруг солнца, находится в связанном состоянии, камни, которые мы на земле можем наблюдать, - в связанном состоянии (они не могутуйти на бесконечность). В этом смысле все окружающие нас объекты в пределах солнечной системы это частицы в связанном состоянии. Единственные объекты, которые отражают несвязанные состояния, это два американских аппарата, которые были запущены лет пятнадцать назад

2) Когда переменная принимает определённые значения (счётное множество дискретных значений), говорят, что эта переменная квантуется.

3) Строго говоря, если быть очень аккуратным, при измерении энергии могут быть получены лишь определённые значения. Это важный нюанс. Квантовая теория не считает, что объект обладает какой-то характеристикой сам по себе, пока мы не пытаемся её измерить. Вот когда мы измеряем ту или иную характеристику, она появляется. Этому есть экспериментальное подтверждение. Если объект имеет сам по себе какие-то характеристики, то можно привести примеры, когда в определённых ситуациях будут получаться определённые следствия, а если он не обладает сам по себе, тогда следствия в тех же ситуациях будут другими. Это положение теории, очень интригующее, неоднократно проверялось – если мы будем считать, что система обладает сама по себе какой-то характеристикой, то из этого можно получить следствия, противоречащие наблюдаемому в действительности. Значит, при измерении энергии могут быть получены лишь определённые значения.

1) Вот сейчас кто-нибудь снаружи дверь закроет на ключ, и мы все в связанном состоянии. И будем рассматривать нас тут сейчас с точки зрения квантовой теории.

1) Напомню постулат Бора. Электрон, который вращается вокруг ядра должен излучать электромагнитные волны, терять энергию и упасть на ядро. Каким образом эта проблема была решена Бором для атома водорода (вы в школе Боровскую модель атома водорода изучали)? Простым. Он постулировал, что есть такие орбиты, на которых электрон не излучает, то есть он там крутится и не излучает. Как это стыковалось с наукой? А никак. В электродинамике известно, что если он крутится – должен излучать, а Бор говорит – не излучает. Понятно, что это не решение проблемы. Как теория эту проблему решила, мы уже сейчас знаем: в стационарных состояниях пространственная конфигурация не меняется, она застывшая (это было видно из решения уравнения Шрёдингера), динамические характеристики есть, импульс, момент импульса, но кинематики нет; распределение вероятности электронов в той или иной точке статично, ему соответствует статичное распределение заряда, а статичное распределение заряда ничего не излучает. Вот таким образом утверждение Бора получается не в виде постулата, а как следствие теории, и электродинамика не страдает – нет никакого вращения.

2) Для сравнения, с точки зрения математики, что такое классическая Ньютоновская механика? Теория дифференциальных уравнений второго порядка (Второй закон Ньютона это дифференциальное уравнение второго порядка). Было такое представление, что Господь Бог в своём всеведении додумался до теории дифференциальных уравнений второго порядка и устроил мир предметный, описываемый этими уравнениями. Когда Кеплер установил свой Первый закон, что планеты движутся по эллипсам, у него было точное ощущение, что он проник в замысел создателя; теория конических сечений была самая развитая и любимая наука ещё с античности, и когда Кеплер обнаружил, что планеты движутся по эллипсам (по коническим сечениям), оказалось, что создатель тоже знал теорию конических сечений и устроил там на небе всю эту замечательную вещь именно таким образом. Мы сейчас увидим, если продолжать эту метафору, что создатель продвинулся ещё и дальше в своём математическом образовании.

3) Звёздочка обозначает комплексное сопряжение.

1) Мы можем иметь два вектора и это столбцы, α и β это числа. Мы можем вектор умножить на α, получим новый вектор, умножить на β, получим новый вектор, взять их сумму (сумма двух матриц-столбцов опять будет матрица-столбец), на то что получится подействовать оператором , мы получим какой-то вектор. А можем сделать иначе: возьмём оператором подействуем на вектор , получим вектор, умножим его на число α, потом оператором подействуем на вектор , получим новый вектор, умножим его на число β и сложим. Если мы получим в результате то же, что и в предыдущем случае, то оператор называется линейным.

1) Чтобы было понятно о чём речь. Я взял с потолка матрицу , она представляет оператор , после этого я эту матрицу изуродовал: взял её транспонировал и заменил каждый элемент комплексно сопряжённым к этому элементу. И оказалось, что так изуродованная матрица совпадает с исходной матрицей. Тогда мы получим тот же самый оператор замечательный оператор, потому что в результате таких манипуляций не всякая матрица перейдёт в себя), которыйназывается эрмитовым или самосопряжённым.

2) Когда оператор действует на какой-то вектор, он его переводит в другой вектор, но, если нам удалось подсунуть оператору такой вектор , что при действии на него оператор даёт тот же самый вектор, умноженный на число, то вот этот, конечно, чем-то замечательный вектор, называется собственным вектором.

3) Осознать надо о чём речь. В любой физической теории задать состояние это значит дать на столько полное описание объекта в рамках данной теории, чтоб дальше можно было ответить на все физически разумные вопросы относительно этого объёкта и предсказать, как это состояние будет эволюционировать. Например, как дать исчерпывающее описание летящей пули? Надо задать её положение и импульс, исходя из этого, можно узнать момент импульса, энергию, можно узнать, как это состояние будет дальше меняться, потому что есть Второй закон Ньютона для этого.«Нет, - говорит квантовая теория, - ты мне задай некий вектор в абстрактном пространстве». Как задать? Дальше нам придётся разобраться, как это делать.

1) Это существенно. Физика ограничивается обсуждением лишь тех величин, которые подлежат измерению, поэтому все её утверждения можно проверить, а утверждения, которые принципиально нельзя проверить (в частности, это утверждения о величинах, которые нельзя измерить), все такие утверждения с точки зрения физики являются бессмысленными, не ошибочными, а бессмысленными. Действительно, это пустая болтовня, если высказывание нельзя проверить в принципе, то чего сотрясать воздух. В окружающем нас языке море высказываний, которые нас окружают на обычном житейском уровне, на самом деле 90% высказываний не проверяемы. Тогда, что же те, кто их произносит, валяют дурака? Нет, они преследуют другую цель, понятно какую – с помощью всех этих высказываний добиться от объекта, на который они направлены, определённого поведения. Физика это островок, где все высказывания осмысленны, проверяемы и прочее, а 90% речевых потоков одного персонажа на другой, они преследуют цель сделать из того, чего я хочу. И тут о высказываниях бессмысленно судить с точки зрения истинности – неистинности, это другая песня совершенно. Они должны судиться по другому критерию: достигают они цели или нет, короче говоря, успешно я навешал лапшу на уши ему или нет. Если, допустим, я вешал, вешал, а он не поддаётся, то да, я валял дурака, а если я добился нужного поведения, то я занимался разумной осмысленной деятельностью. Эти вещи полезно понимать, для того, например, чтобы не ввязываться в бессмысленные споры. Пытаясь оценивать все эти вещи с точки зрения истинности – ложности, справедливости – несправедливости, скорее сами поддаёмся.

1) Проблема какая? У нас летит пуля, а нам надо в абстрактном пространстве придумать вектор, который соответствует вот этой конкретной пуле. Как вообще задать вектор в обычном пространстве? Вот вектор – стрелка, я представляю, как сообщить по телефону, что вот у меня тут вектор передо мной. Вектор задаётся в нормальном пространстве тройкой чисел, где взять три числа? Если у нас есть базисные векторы, то любой вектор задаётся тремя числами. Как задать базис, как сообщить по телефону базис? На базис можно лишь указать пальцем, вот в реальном пространстве мы должны выбрать три вектора, тогда любой другой задаётся, можно и по телефону передать базис. Можно сказать: «Возьми камушек, подвесь на нитке, тогда вектор, идущий из камушка вдоль нитки, это будет вектор а потом построй вектор перпендикулярно по правилу правого винта это будет вектор После этого сообщаете три числа, и он там у себя слепил вектор, который вы видите перед собой. В абстрактном пространстве нет отвесов, нет компасов, нет ничего. Как там задать базис? Есть способ. В качестве базиса мы можем выбрать собственные векторы какого-либо оператора.

1) действует, и получается «ку-ку».

2) Когда символ q сидит под скобками – это просто метка, а q перед вектором – это число, то есть векторы помечены собственными значениями.

3) Действуем оператором на некоторый вектор, мы получим какой-то вектор, на этот вектор действуем оператором и .

4) В житейском плане: оператор – одеть пиджак, оператор – одеть пальто, понятно, что эти операторы не коммутируют, а оператор – одеть шапку, оператор – одеть ботинки, они коммутируют, понятно, результат один и тот же, в какой последовательности ни выполняй.

1) Единичный оператор – это такой оператор, который любой вектор переводит в себя:

2) Так следует из этой теории, а что касается физики, то действительно нет никаких указаний на то, что координаты квантуются. Хотя идеи о том, что пространство и время могут квантоваться, были и, может быть, ещё остаются, но пока никаких указаний на это нет. Вполне могло бы быть, что пространство ячеистое, но ещё раз повторяю пока в казённой теории координаты не квантуются, и, в общем-то, нет особой потребности в модификации этой теории.

1) Мы сейчас пролезли в это абстрактное пространство, где живут векторы и операторы. Мы изобразили вектор для определённого физического состояния: изготовили частицу с импульсом и энергией E, и мы для неё нарисовали вектор в абстрактном пространстве.

2) А теперь мы думаем, что получится, когда оператором действуем на вектор – это собственные векторы оператора

3) Здесь не так просто: мы не знаем, как действует оператор на вектор , верно следующее равенство.

1) Конечно, вопрос сразу может возникнуть, как понимать функцию от оператора? В конце концов, всякая функция выражается степенными рядами, например даст:

1) Проверка:

1) Кстати, ответ на этот вопрос вы уже можете знать только на основании того, что мы уже здесь обсуждали (вот, если вы удерживаете в голове всю цепочку, то ответ можно дать). У нас было коммутационное соотношение из этого математического факта следовало, что координата не квантуется, ну и импульс, надо ожидать, не будет квантоваться, потому что буквы и равноправны.

¹) Что даст скалярное произведение собственного вектора оператора координаты с собственным вектором оператора импульса?

Тогда другой вопрос: скалярное произведение двух собственных векторов оператора импульса. Ответ, он ясен заранее, если это разные векторы, то их скалярное произведение должно равняться нулю (собственные векторы ортогональны), посмотрим, как это сработает. Сначала (кстати, нельзя сказать, чему равен этот вектор, это просто разложение по координате). Тогда мы имеем: не совпадает с C. Итак,

1) Это интересное чисто математическое следствие, но у нас нет времени, и я просто приведу результат.

1) Наглядно предметы, показывающие магнитный момент – стрелка компаса. Почему стрелка компаса показывает на север? Потому что магнитный момент ориентируется вдоль силовой линии. Если мы имеем магнит с такими силовыми линиями, то магнитный момент (стрелка компаса) ориентируется вдоль силовой линии, и на неё будет действовать сила

2) Ось z задаёт направление поля, а