История изучения капиллярных и поверхностных сил
| Загрузить архив: | |
| Файл: 240-0259.zip (84kb [zip], Скачиваний: 40) скачать |
Введение.
Если стеклянная трубка, столь же узкая внутри, как волос (лат. capillus), погружается в воду, то жидкость поднимается внутри трубки до высоты большей, чем снаружи. Эффект не мал: высота поднятия около 3 см в трубке с каналом в 1 мм. Это кажущееся нарушение законов гидростатики (открытке которых было достижением науки XVII в.) вызвало на пороге XVIII в. возрастающий интерес к капиллярным явлениям. Интерес был двояким. Во-первых, хотелось видеть, можно ли охарактеризовать поверхности жидкостей и твердых тел некоторым простым механическим свойством, таким, как состояние натяжения, которое могло бы объяснить наблюдаемые явления. Следовало объяснить, например, почему вода в трубке поднимается, тогда как ртуть опускается; почему поднятие воды между параллельными пластинами вдвое меньше, чем в трубке с диаметром, равным расстоянию между пластинами; почему поднятие обратно пропорционально этому диаметру. Вторая причина интереса происходила из понимания того, что наблюдались эффекты, которые должны возникать в результате действия сил между частицами вещества, и что изучение этих эффектов, следовательно, должно дать какие-то сведения о таких силах и, возможно, о самих частицах.
До появления теорий Юнга и Лапласа.
Первооткрывателем капиллярных явлений считается Леонардо да Винчи (Leonardo da Vinci). Однако первые аккуратные наблюдения капиллярных явлений на трубках и стеклянных пластинках были проделаны Фрэнсисом Хоксби в 1709 году [1]).
То, что вещество не является бесконечно делимым и имеет атомную или молекулярную структуру, было рабочей гипотезой для большинства ученых начиная с XVIII в. К концу XIX в., когда группа физиков, сторонников позитивистской философии, указала, каким непрямым являлось доказательство существования атомов, на их заявление последовала лишь незначительная реакция, и в итоге их возражения не были опровергнуты до начала этого столетия. Если в ретроспективе к сомнения кажутся нам неосновательными, мы должны помнить, что почти все, кто тогда верил в существование атомов, верили также твердо в материальное существование электромагнитного эфира, а в первой половине XIX в. — часто и теплорода. Тем не менее ученые, внесшие наибольший вклад в теорию газов и жидкостей, использовали предположение (обычно в явной форме) о дискретной структуре вещества. Элементарные частицы материи называли атомами, или молекулами (например, Лаплас), или просто частицами (Юнг), но мы будем следовать современным понятиям и употреблять слово «молекула» для элементарных частиц, составляющих газ, жидкость или твердое тело.
В начале XIX в. силы, которые могли бы существовать между молекулами, были так же не ясны, как и сами частицы. Единственной силой, в отношении которой не было сомнения, была ньютоновская гравитация. Она действует между небесными телами и, очевидно, между одним таким телом (Землей) и другим (например, яблоком), имеющим лабораторную массу; Кавендиш незадолго до этого показал, что она действует и между двумя лабораторными массами, а потому предполагалось, что она действует также между молекулами. В ранних работах по жидкостям можно найти массы молекул и плотности масс, входящие в уравнения, в которых мы теперь должны писать числа молекул и плотности чисел молекул. В чистой жидкости все молекулы имеют одинаковую массу, так что это различие не играет роли. Но еще до 1800 г. было ясно, что понятия о гравитационных силах недостаточно для объяснения капиллярных явлений и других свойств жидкостей. Поднятие жидкости в стеклянной трубке не зависит от толщины стекла (по данным Хоксби[1][D&L1], 1709 г.), и, таким образом, только силы со стороны молекул в поверхностном слое стекла действуют на молекулы в жидкости. Гравитационные же силы лишь обратно пропорциональны квадрату расстояния и, как было известно, действуют свободно через промежуточное вещество.
Природа межмолекулярных сил, отличных от сил тяготения, была весьма неясной, но в измышлениях не было недостатка. Священник-иезуит Роджер Боскович (Ruggero Giuseppe Boscovich) полагал, что молекулы отталкиваются на очень малых расстояниях, притягиваются при несколько больших расстояниях и затем по мере увеличения расстояния демонстрируют попеременно отталкивание и притяжение со все уменьшающейся величиной. Его идеи в следующем столетии оказали влияние как на Фарадея, так и на Кельвина, но были слишком сложными, чтобы оказаться непосредственно полезными для тех, кто занимался теорией капиллярности. Последние благоразумно довольствовались простыми гипотезами.
Куинк (G.H.Quincke) поставил эксперименты по определению наибольшего расстояния, на котором действие межмолекулярных сил ощутимо. Он получил, что для различных веществ эти расстояния составляют ~ 1/20000 часть миллиметра, т.е. ~ 5·10–6см (данные приведены согласно [2]).
Джеймс Джурин показал, что высота, на которую поднимается жидкость, определяется верхней частью трубки, которая находится над жидкостью, и не зависит от формы нижней части трубки. Он считал, что поднятие жидкости происходит благодаря притяжению со стороны внутренней цилиндрической поверхности трубки, к которой примыкает верхняя поверхность жидкости. Исходя из этого, он показал, что поднятие жидкости в трубках из одинакового вещества обратно пропорционально их внутреннему радиусу [3].
Клеро был одним из первых, кто показал необходимость принятия во внимание притяжения между частицами самой жидкости для объяснения капиллярных явлений [4]. Он, однако, не признавал, что расстояния, на которых действуют эти силы, неощутимо малы.
В 1751 г. фон Сегнер ввел важную идею поверхностного натяжения по аналогии с механическим натяжением мембраны в теории упругости [5]. Сегодня понятие поверхностного натяжения является заурядным, с него обычно начинают изучение капиллярных сил и поверхностных явлений в учебных заведениях.
Эта идея стала ключевой в дальнейшем развитии теории. Собственно, тем самым был сделан первый шаг в изучении явления — введено феноменологическое понятие, описывающее макроскопическое поведение системы. Второй шаг — это вывод феноменологических понятий и вычисление значений величин, исходя из молекулярной теории. Этот шаг имеет огромную важность, так как является проверкой правильности той или иной молекулярной теории.
В 1802 г. Джон Лесли привел первое корректное объяснение подъема жидкости в трубке, рассматривая притяжение между твердым телом и тонким слоем жидкости на его поверхности [6]. Он, в отличие от большинства предыдущих исследователей, не предполагал, что сила этого притяжения направлена вверх (непосредственно для поддержания жидкости). Напротив, он показал, что притяжение всюду нормально к поверхности твердого тела.
Прямой эффект притяжения — увеличение давления в слое жидкости, находящемся в контакте с твердым телом, так, что давление становится выше, чем внутри жидкости. Результатом этого является то, что слой стремится “растечься” по поверхности твердого тела, останавливаемый лишь силами гравитации. Таким образом, стеклянная трубка, погруженная в воду, смачивается водой всюду, куда та “смогла доползти”. Поднимаясь, жидкость образует столб, вес которого в конце концов уравновешивает силу, порождающую растекание жидкости.
Эта теория не была записана с помощью математических символов и поэтому не могла показать количественную связь между притяжением отдельных частиц и конечным результатом. Теория Лесли была позднее переработана с применением лапласовских математических методов Джеймсом Ивори (James Ivory)в статье о capillary action, under “Fluids, Elevation of”, в приложении к 4-му изданию Encyclopaedia Britannica, опубликованном в 1819 г.
Теории Юнга и Лапласа.
В 1804 г. Томас Юнг [7] обосновал теорию капиллярных явлений на принципе поверхностного натяжения. Он также наблюдал постоянство угла смачивания жидкостью поверхности твердого тела (краевого угла) и нашел количественное соотношение, связывающее краевой угол с коэффициентами поверхностного натяжения соответствующих межфазных границ. В равновесии контактная линия не должна двигаться по поверхности твердого тела, а значит, говорил
 (1)
(1)
где sSV,sSL,sLV— коэффициенты поверхностного натяжения межфазных границ твердое тело – газ (пар), твердое тело – жидкость, жидкость – газ соответственно, q— краевой угол. Это соотношение теперь известно как формула Юнга. Эта работа все же не оказала такого влияния на развитие науки в этом направлении, какое оказала вышедшая несколькими месяцами позже статья Лапласа (Pierre Simon Laplace). Это, по-видимому, связано с тем, что Юнг избегал использования математических обозначений, а пытался описывать все словесно, отчего его работа кажется запутанной и неясной. Тем не менее он считается сегодня одним из основателей количественной теории капиллярности.
Явления когезиии адгезии , конденсация пара в жидкость, смачивание твердых тел жидкостями и многие другие простые свойства вещества — все указывало на наличие сил притяжения, во много раз более сильных, чем гравитация, но действующих только на очень малых расстояниях между молекулами. Как говорил Лаплас, единственное вытекающее из наблюдаемых явлений условие, налагаемое на эти силы, состоит в том, что они «неощутимы на ощутимых расстояниях».
Силы отталкивания создавали больше хлопот. Их наличие нельзя было отрицать— они должны уравновешивать силы притяжения и препятствовать полному разрушению вещества, но их природа была совершенно неясной. Вопрос осложнялся двумя следующими ошибочными мнениями. Во-первых, часто считалось, что действующей силой отталкивания является тепло (как правило, мнение сторонников теории теплорода), поскольку (такова была аргументация) жидкость при нагревании сначала расширяется и затем кипит, так что молекулы разъединяются на гораздо большие расстояния, чем в твердом теле. Второе ошибочное мнение возникло из уводящего назад к Ньютону представления, согласно которому наблюдаемое давление газа происходит вследствие статического отталкивания между молекулами, а не из-за их столкновений со стенками сосуда, как тщетно доказывал Даниель Бернулли.
На этом фоне было естественно, что первые попытки объяснить капиллярность или вообще сцепление жидкостей основывались на статических аспектах вещества. Механика была хорошо понимаемой теоретической ветвью науки; термодинамика и кинетическая теория были еще в будущем. В механическом рассмотрении ключевым было предположение о больших, но короткодействующих силах притяжения. Покоящиеся жидкости (в капиллярной ли трубке или вне ее) находятся, очевидно, в равновесии, а потому эти силы притяжения должны уравновешиваться силами отталкивания. Поскольку о них можно было сказать еще меньше, чем о силах притяжения, их часто обходили молчанием, и, говоря словами Рэлея, «силам притяжения предоставлялось исполнять немыслимый трюк уравновешивания самих себя». Лаплас[2] первым удовлетворительно разрешил эту проблему [8], полагая, что силы отталкивания (тепловые, как он допускал) можно заменить внутренним давлением, которое действует повсеместно в несжимаемой жидкости. (Это предположение приводит временами к неопределенности в работах XIX в. в отношении того, что строго понимается под «давлением в жидкости».) Приведем расчет внутреннего давления по Лапласу. (Этот вывод ближе к выводам Максвелла [2] и Рэлея [10]. Вывод приводится по [9] .)
Оно должно уравновешивать силы сцепления в жидкости, и Лаплас отождествлял это с силой на единицу площади, которая оказывает сопротивление разделению бесконечного жидкого тела на два далеко разъединяемых полубесконечных тела, ограниченных плоскими поверхностями. Приведенный ниже вывод ближе к выводам Максвелла и Рэлея, чем к оригинальной форме Лапласа, но существенного различия в аргументации нет.
Рассмотрим два полубесконечных
тела жидкости со строго плоскими поверхностями, разделенные прослойкой
(толщины l) пара с пренебрежимо малой плотностью
(рис. 1), и в каждом из них выделим элемент объема. Первый находится в верхнем
теле на высоте r
над плоской поверхностью нижнего тела; его объем равен dxdydz. Второй находится в нижнем теле и имеет объем  f(s)— сила, действующая между двумя молекулами,
разделенными расстоянием s,
а d -
радиус ее действия. Поскольку это всегда сила притяжения, имеем
f(s)— сила, действующая между двумя молекулами,
разделенными расстоянием s,
а d -
радиус ее действия. Поскольку это всегда сила притяжения, имеем

Если r — плотность числа молекул в обоих телах, то вертикальная составляющая силы взаимодействия двух элементов объема равна
 (2)
(2)
Полная сила притяжения, приходящаяся на единицу площади (положительная величина), есть
 (3)
(3)
Пусть u(s) — потенциал межмолекулярной силы:
 (4)
(4)
 (5)
(5)

Рис. 1.
Интегрируя по частям еще раз, получаем
 (6)
(6)
Внутреннее давление Лапласа Kесть сила притяжения на единицу площади между двумя плоскими поверхностями при их контакте, т.е. F(0):
 (7)
(7)
где  — элемент
объема, который можно записать как
— элемент
объема, который можно записать как  u(r) по
предположению всюду отрицательно или равно нулю, то Kположительно.Лаплас полагал, что Kвелико по
сравнению с атмосферным давлением, но первую реалистическую численную
оценку предстояло сделать Юнгу.
u(r) по
предположению всюду отрицательно или равно нулю, то Kположительно.Лаплас полагал, что Kвелико по
сравнению с атмосферным давлением, но первую реалистическую численную
оценку предстояло сделать Юнгу.
Приведенныйвыше вывод основан на неявном допущении, что молекулы распределены равномерно с плотностьюr, т.е. жидкость не обладает различимой структурой в шкале размеров, соизмеримых с радиусом действия силd.Без этого предположения нельзя было бы написать выражения (2) и (3) в такой простой форме, а надо было бы выяснить, как присутствие молекулы в первом элементе объема влияет на вероятность наличия молекулы во втором.
Натяжение на единицу длины вдоль произвольной линии на поверхности жидкости должно быть равным (в соответствующей системе единиц) работе, затраченной на создание единицы площади свободной поверхности. Это следует из опыта по растяжению пленки жидкости (рис. 2).

Рис. 2.
На проволочной рамке держится жидкая пленка, прикрепленная правым краем к свободно перемещаемой проволочке. Сила F, необходимая для уравновешивания натяжения в двусторонней пленке, пропорциональна длине L. Пусть F = 2sL. Смещениепроволочки на расстояние symbol SYMBOL f "Symbol" s 12xтребует работы Fsdx = sdA, где dA — увеличение площади. Таким образом, натяжение на единицу длины на отдельной поверхности, или поверхностное натяжение s, численно равно поверхностной энергии на единицу площади.
Величина этой работы может быть сразу получена из выражения (6) для F(l). Если взять два полубесконечных тела в контакте и развести их на расстояние, превышающее радиус действия межмолекулярных сил, работа на единицу площади будет определяться как
 (8)
(8)
При разделении образуются две свободные поверхности, и потому затраченную работу можно приравнять удвоенной поверхностной энергии на единицу площади, которая равна поверхностному натяжению:
 (9)
(9)
Таким образом, K естьинтеграл от межмолекулярного потенциала, или его нулевой момент, а H — его первый момент.В то время как K недоступно прямому эксперименту, H может быть найдено, если мы сможем измерить поверхностное натяжение.
Пусть SYMBOL 102 f "Symbol"когезионной энергии в некоторой точке жидкости или газа, т.е. отношение dСИМВОЛ 100 f "Symbol"U/dСИМВОЛ 100 f "Symbol"V где dСИМВОЛ 100 f "Symbol"U — внутренняя энергия малого объема SYMBOL 100 f "Symbol"V жидкости или газа, содержащего эту точку. Для молекулярной модели принимаем
 (10)
(10)
где r — расстояние от рассматриваемой точки. Рэлей отождествлял лапласовское K с разностью этого потенциала 2SYMBOL 102 f "Symbol"2SYMBOL 102 f "Symbol"S) и точкой внутри (значение 2SYMBOL 102 f "Symbol"I). На поверхности интегрирование в (10) ограничено полусферой радиуса d, а во внутренней области проводится по всей сфере. Следовательно, SYMBOL 102 f "Symbol"S есть половина SYMBOL 102 f "Symbol"I, или
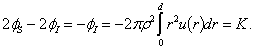 (11)
(11)
Рассмотрим теперь каплю радиуса R. Расчет fIСИМВОЛ
102 f "Symbol"fS
интегрирование теперь проводится по более ограниченному объему из-за кривизны
поверхности. Если SYMBOL 113 f "Symbol"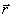 и фиксированным радиусом
и фиксированным радиусом

 (12)
(12)
Тогда внутреннее давление в капле есть
 (13)
(13)
где H определяется уравнением (9). Если бы мы взяли не сферическую каплю, а порцию жидкости с поверхностью, определяемой двумя главными радиусами кривизны R1 и R2 , то получили бы внутренне давление в виде
 (14)
(14)
По теореме Эйлера сумма  равна сумме обратных
радиусов кривизны поверхности вдоль любых двух ортогональных касательных.
равна сумме обратных
радиусов кривизны поверхности вдоль любых двух ортогональных касательных.
Так как K и H положительны и R положительно для выпуклой поверхности, то из (13) следует, что внутреннее давление в капле выше, чем в жидкости с плоской поверхностью. Наоборот, внутреннее давление в жидкости, ограниченной вогнутой сферической поверхностью ниже, чем в жидкости с плоской поверхностью, поскольку R в этом случае отрицательно.
Эти результаты составляют основу теории капиллярности
Лапласа. Уравнение для разности давлений  (давление жидкости
внутри сферической капли радиуса R) и
(давление жидкости
внутри сферической капли радиуса R) и  (давление газа
снаружи) теперь называют уравнением Лапласа:
(давление газа
снаружи) теперь называют уравнением Лапласа:
 (15)
(15)
Достаточно трех идей — натяжения у поверхности, внутреннего давления и краевого угла, а также выражений (1) и (15), чтобы решить все задачи обычной равновесной капиллярности методами классической статики. Таким образом, после работ Лапласа и Юнга основы количественной теории капиллярности были заложены.
Результаты Юнга были получены позже Гауссом вариационным методом. Но все эти работы (Юнга, Лапласа и Гаусса) обладали одним общим недостатком, изъяном, если можно так выразиться. Об этом недостатке будет рассказано позже.
При расчете давления внутри искривленной жидкой поверхности был введен потенциал Рэлея 2SYMBOL 102 f "Symbol"SYMBOL 102 f "Symbol"I является плотностью когезионной энергии. Впервые это полезное понятие в 1869 г. ввел Дюпре, который определил его как работу дробления куска вещества на составляющие его молекулы (la travail de dйsagrйСИМВОЛ 233 f "Times New Roman CE"gation totale — работа полной дезагрегации).

Рис. 3
Направленная внутрь сила,
действующая на молекулу на глубине r Он приводит [12] вывод, проделанный его коллегой
Ф.Ж.Д.Массье следующим образом.
Сила, действующая на молекулу у поверхности по направлению к объему жидкости,
противоположна по знаку силе, возникающей от заштрихованного объема на рис. 3,
поскольку внутри жидкости сила притяжения от шарового объема радиуса равна нулю
из симметрии. Таким образом, сила, направленная внутрь, есть Эта сила положительна, так как f(0 поскольку u(r)
— четная функция. Эта работа равна минус удвоенной энергии на молекулу,
необходимой для дезинтеграции жидкости (удвоенной,
чтобы не считать молекулы дважды: один раз при их удалении, другой раз — как
часть среды): Это простое и понятное выражение для
внутренней энергии U жидкости, содержащей N молекул. Отсюда следует, что плотность когезионной
энергии SYMBOL 102 f "Symbol" что совпадает с (11), если убрать
индекс I. Сам Дюпре получил тот же
результат окольным путем. Он рассчитывал dU/dV
через работу против межмолекулярных сил при однородном расширении куба
жидкости. Это дало ему Поскольку K имеет
форму то интегрирование (20) снова
приводит к (19). Рэлей критиковал вывод Дюпре [10].
Он считал, что рассмотрение работы однородного расширения от состояния
баланса когезионных и отталкивающих межмолекулярных
сил при учете только когезионных сил было необоснованным;
прежде чем предпринять подобный шаг, следовало бы располагать лучшим знанием
вида сил отталкивания. Мы видим, что в этом выводе, как и в выводах Юнга, Лапласа и
Гаусса, существенным образом используется предположение о скачкообразном
изменении плотности числа молекул вещества на границе раздела фаз. В то же
время, чтобы проведенные рассуждения описывали реальные явления в веществе,
необходимо предполагать, что радиус действия межмолекулярных сил в веществе
много больше характерного расстояния между частицами. Но при этом
предположении граница раздела двух фаз не может быть резкой — должен возникнуть
непрерывный переходный профиль плотности, иначе говоря, переходная зона[3]. Были предприняты попытки обобщить эти выводы на непрерывный
переходный профиль. В частности, Пуассон, пытаясь пойти по такому пути, пришел
к ошибочному выводу, что при наличии переходного профиля поверхностное
натяжение должно вообще исчезнуть. Позже Максвелл показал ошибочность такого
вывода. Однако, само предположение о том, что радиус действия
межмолекулярных сил в веществе много больше характерного расстояния между
частицами не соответствует экспериментальным данным. В действительности, эти
расстояния одного порядка. Поэтому механистическое рассмотрение в духе
Лапласа является, говоря современным языком, теорией среднего поля. Таковой же
является не описанная здесь теория Ван-дер-Ваальса, давшая знаменитое уравнение
состояния реальных газов. Во всех этих случаях точный расчет требует учета корелляций между плотностями количества частиц в
различных точках. Это делает задачу очень сложной. Как часто бывает, термодинамическое описание оказывается
более простым и более общим, не будучи ограниченным недостатками конкретных
моделей. Именно таким образом описал капиллярность Гиббс в
1878г., построив чисто термодинамическую теорию [12].Эта теория стала неотъемлемой частью гиббсовской
термодинамики.Теория
капиллярности Гиббса, не опираясь непосредственно на какие-либо
механистические модели,лишена недостатков
теории Лапласа; она
может по праву считаться первой детально развитой термодинамической теорией
поверхностных явлений. Про теорию капиллярности Гиббса
можно сказать, что она очень проста и очень сложна. Проста потому, что Гиббсу
удалось найти метод, позволяющий получить наиболее компактные и изящные
термодинамические соотношения, в равной мере применимые к плоским и
искривленным поверхностям. «Одной из основных задач теоретического
исследования в любой области знания, —
писал Гиббс, — является установление
такой точки зрения, с которой объект исследования проявляется с наибольшей
простотой» [13]. Такая точка зрения в теории
капиллярности Гиббса — это представление
о разделяющих поверхностях. Использование наглядного геометрического образа
разделяющей поверхности и введение избыточных величин позволило максимально
просто описать свойства поверхностей и обойти вопрос о структуре и толщине
поверхностного слоя, который во времена Гиббса был совершенно не изучен и до
сих пор остается решенным далеко не полностью. Избыточные величины Гиббса
(адсорбция и другие) зависят от положения разделяющей поверхности, и последнее
может быть также найдено из соображений максимальной простоты и удобства. Разумно выбирать в каждом случае
разделяющую поверхность так, чтобы она была всюду перпендикулярна градиенту
плотности. Если разделяющие поверхности выбраны, то каждой фазе {l} (l = a,
b,
g)
теперь соответствует занимаемый ей объем V{l}. Полный объем
системы Пусть где Гиббс использовал два основных положения разделяющей
поверхности: такое, при котором адсорбция одного из компонентов равна нулю
(сейчас эту поверхность называют эквимолекулярной), и положение, для
которого исчезает явная зависимость поверхностной энергии от кривизны
поверхности (это положение было названо Гиббсом поверхностью натяжения).
Эквимолекулярной поверхностью Гиббс пользовался для рассмотрения плоских
жидких поверхностей (и поверхностей твердых тел), а поверхностью
натяжения— для рассмотрения искривленных поверхностей. Для обоих
положений сокращается число переменных и достигается максимальная
математическая простота. Теперь о сложности теории Гиббса. Будучи очень простой в
математическом отношении, она все же трудна для восприятия; происходит это
по нескольким причинам. Во-первых, теорию капиллярности Гиббса невозможно понять
в отрыве от всей гиббсовской термодинамики, в основе
которой лежит весьма общий, дедуктивный метод. Большая общность теории всегда
придает ей некоторую абстрактность, что, конечно, отражается на легкости
восприятия. Во-вторых, сама теория капиллярности Гиббса есть обширная, но
условная система, требующая единства восприятия без отвлечения от отдельных ее
положений. Дилетантский подход к изучению Гиббса просто невозможен. Наконец,
немаловажным обстоятельством является то, что вся упомянутая работа Гиббса
написана весьма конспективно и очень трудным языком. Эта работа, по словам Рэлея,
«слишком сжата и трудна не только для большинства, но, можно сказать, для всех
читателей» [15]. По мнению Гугенгейма, «гораздо легче использовать формулы Гиббса, чем
понимать их» [16]. Естественно, что использование формул Гиббса без их
истинного понимания приводило к появлению многочисленных ошибок в
интерпретации и применении отдельных положений теории капиллярности Гиббса.
Много ошибок было связано с непониманием необходимости однозначного определения
положения разделяющей поверхности для получения правильного физического результата.
Ошибки такого рода часто встречались при анализе зависимости поверхностного
натяжения от кривизны поверхности; не избежал их даже один из «столпов»
теории капиллярности— Баккер. Пример ошибок другого рода — неправильная интерпретация химических потенциалов при рассмотрении
поверхностных явлений и внешних полей. Уже вскоре после опубликования теории капиллярности Гиббса
высказывались пожелания о ее более полном и подробном пояснении в научной
литературе. В цитированном выше письме к Гиббсу Рэлей предлагал, чтобы эту
работу взял насебясам Гиббс. Однако выполнено это было
значительно позже: Райс подготовил комментарий ко
всей теории Гиббса [17 стр. 505—708], а отдельные ее положения комментировались
в трудах Фрумкина, Дефея, Ребиндера,
Гуггенгейма, Толмена, Баффа, Семенченко и других
исследователей. Многие положения теории Гиббса прояснились, и для их обоснования
были найдены более простые и эффективные логические приемы. Типичным примером является эффектная работа Кондо [18], в которой был предложен наглядный и простой
для понимания метод введения поверхности натяжения путем мысленного
перемещения разделяющей поверхности. Если мы напишем выражение для энергии
равновесной двухфазной системыa – b (a— внутренняя и b
—наружная фазы) со сферической поверхностью
разрыва U=TS – PaVa – PbVb+ sA + и будем мысленно менять положение разделяющей
поверхности, т.е. менять ее радиусr,
то, очевидно, такие физические характеристики, как энергия U, температура Т, энтропия S, давление Р,
химический потенциал i-го компонента mi и егомасса mi, а также полный объем системы Va + Vbпри этом не
изменяется. Что же касается объемаVa=4/3pr3 и площади A=4pr2 и
поверхностного натяжения s,
то эти величины будут зависеть от положения разделяющей поверхности и потому
для указанного мысленного процесса изменения rмы получаем из (22) – Pa dVa+ Pb dVb + sdA + Ads =0 (23) или Уравнение (24) определяет нефизическую (это обстоятельство
отмечено звездочкой) зависимость поверхностного натяжения от положения
разделяющей поверхности. Эта зависимость характеризуется единственным
минимумом s, который и соответствует
поверхности натяжения. Таким образом, по Кондо, поверхность
натяжения — эта такая разделяющая поверхность,
для которой поверхностное натяжение имеет минимальное значение. Гиббс вводил поверхность натяжения иным путем. Он исходил из
основного уравнения теории капиллярности (черта сверху означает избыток для
произвольной разделяющей поверхности с главными кривизнами
С1 и C2 ) и рассматривал физический (а не чисто мысленный) процесс
искривления поверхности при заданном ее положении и фиксированных внешних
условиях. По Гиббсу, поверхности натяжения соответствует такое положение
разделяющей поверхности, при котором искривление поверхностного слоя при постоянстве
внешних параметров не сказывается на поверхностной энергии и соответствует
также условию: ¶s/¶r =0 (26) Гуггенгейм так комментирует доказательство
Гиббса: «Я нашел рассмотрение Гиббса трудным, и чем тщательнее я изучал его,
тем более неясным оно мне казалось» [16]. Это признание свидетельствует о том, что
понимание поверхности натяжения по Гиббсу встречало трудности даже у
специалистов в области термодинамики. Что касается подхода Кондо, то он
понятен с первого взгляда. Однако необходимо убедиться, что поверхности натяжения
по Гиббсу и Кондо адекватны. Это можно продемонстрировать,
на где Pt — локальное значение тангенциальной
составляющейтензора давления;
r' — радиальная координата; радиусы Ra
и Rb ограничивают
поверхностный слой. Дифференцирование (27) при мысленном перемещении разделяющей поверхности
и постоянстве физического состояния (подход Кондо)
приводит к уравнению (24). Дифференцирование
же при искривлении поверхностного слоя и постоянстве физического состояния
(подход Гиббса, в этом случае Raи Rbпеременны) дает где учтено, что Pt (Pa)=Paи Pt (Pb)=Pb. Из уравнений (28) и (24) видно, что условие (26) эквивалентно условию (ds/dr)*=0 и, следовательно, более простой
и наглядный подход Кондо адекватен подходу Гиббса. Введение понятия разделяющей поверхности позволило
математически строго определить ранее чисто интуитивное понятие границы раздела
фаз и, значит, использовать точно определенные величины в уравнениях. В
принципе, термодинамика поверхностных явлений Гиббса описывает очень широкий
круг явлений, и поэтому (кроме осознания, переформулировок,
более изящных выводов и доказательств) со времени ее создания было сделано
очень мало нового в этой области. Но все же, некоторые результаты, касающиеся
в основном тех вопросов, которые не были освещены Гиббсом, обязательно должны
быть упомянуты. Первоначально метод слоя конечной
толщины, основанный трудами Ван-дер-Ваальса [20], Баккера [21], Версхаффельта [22] и Гуггенгейма [16],
развивался как независимый методтермодинамики
поверхностных явлений. Позднее было обращено внимание на то, что при строгой
формулировке этого метода требуется привлечение понятия разделяющей поверхности,
но при этом используется не одна, а две разделяющих поверхности [23].
Еще большая связь с методом Гиббса проявляется при построении термодинамики
искривленных поверхностей методом слоя конечной толщины [24, 25], где, как и в методе Гиббса, используется понятие поверхности
натяжения. Рассмотрим равновесную двухфазную систему a – bплоской поверхностью разрыва, состояние
которой характеризуется уравнением dU = TdS
– PdV + sdA + и введем разделяющую поверхность со
стороны фазы a,
а также другую разделяющую поверхность со стороны фазы b на произвольном расстоянии tдруг
от друга. Представим, что части системы, разделенные слоем толщины t, заполнены объемными фазамиa,bи их состояние описывается уравнениями: dUa = TdS a – PdV a + sdA + dUb = TdS b – PdV b + sdA + Если мы теперь вычтем (11)
и (12) из
(10), то получим уравнение в котором каждая экстенсивная
величина, помеченная чертой сверху, относится к объему Vs=Atи представляет собой сумму
реальной величины для данного объема и избытков со стороны обеих фаз. Например где
Очевидно, форма
уравнения (32) не зависит от положения разделяющих поверхностей и величины t. При t Весь термодинамический аппарат строится на совместном
рассмотрении уравнений (30) – (32) и вытекающих из них
соотношений. В пределе t Наиболее известным результатом теории капиллярности Гиббса
является уравнение адсорбции где
Гi — абсолютная адсорбция i-го компонента. Это уравнение было получено Гиббсом только для жидких
поверхностей. Оно относится к поверхности натяжения и справедливо как для
плоских, так и для искривленных поверхностей. В течение минувшего столетия уравнение адсорбции Гиббса
многократно обобщалось и каждая его новая форма была вехой в развитии
термодинамики поверхностных явлений, а также этапом лучшего понимания самой
теории Гиббса. Последнее несомненно при рассмотрении обобщенной формы
уравнения адсорбции Гиббса для произвольного положения сферической разделяющей
поверхности [18, 27, 28]: Следует отметить, что уравнение (35) является лишь обобщением формы уравнения адсорбции Гиббса и
физически совершенно эквивалентно уравнению
(34). Более того, можно сказать, что, уступая уравнению (34) в простоте, уравнение (35) и усложняет интерпретацию величиныs,
поскольку утрачивается аналогия с натяжением упругой мембраны. Строго говоря,
термин «поверхностное натяжение» применим только к поверхности натяжения. Другой обобщенной и также физически эквивалентной формой
является запись уравнения адсорбции Гиббса для слоя конечной толщины [24] Ads= где Va
и Vb—
части объема Vs
поверхностного слоя, разделенные поверхностью натяжения. В случае плоской поверхности уравнение (17) принимает вид [4, 17, 18] и
соответствует уравнению (32). Выше мы указывали, что уравнение (34) было получено Гиббсом для границы флюидных фаз.
Соответствующее уравнение для плоской твердой поверхности в изотропном
состоянии было выведено Эрикссоном [30] где
g
— механический аналог поверхностного натяжения жидкости (истинное поверхностное
натяжение твердого тела);
s
— термодинамический аналог поверхностного натяжения жидкости (условное поверхностное
натяжение твердого тела). В общем случае анизотропной поверхности твердого тела
уравнение адсорбции принимает вид [26, 27] где
В уравнении (39) суммирование
производится по всем подвижным компонентам. Что касается неподвижных компонентов,
образующих решетку твердого тела, то их химические потенциалы не фигурируют в
уравнении (39). Гиббс вообще не вводил
понятия химический потенциал неподвижного компонента. Его можно определить
лишь условно и отдельно для каждого направления разреза твердого тела как
химический потенциал в равновесной флюидной фазе, контактирующейс твердым телом по данному разрезу.
Определенный таким образом химический потенциал неподвижного компонента mi'зависит
в каждой точке тела от направления нормали
Кроме того, даже в состоянии
истинного равновесия величина mi не будет одинаковой
для всех точек разреза и поэтому при переходе к избыточным величинам для
межфазной поверхности приходится брать избыток от произведения химического потенциала
на массу неподвижного компонента. Для каждогонаправления причем существует соотношение [31, 32] где gn — натяжение на поверхности в направлении Подстановка (41) в (39) приводит к уравнению [31, 32] которое также является обобщением
уравнения адсорбцииГиббса на
случай твердой поверхности, но сформулировано в терминах избыточного поверхностного
напряжения. Дляжидкой поверхности При применении уравнения адсорбции Гиббса к поверхности
жидкого электрода в нем появляется дополнительный член, связанный с изменением
электрического потенциала. Можно сказать, что для изотермо-изобарических
условий этот член был получен самим Гиббсом, поскольку он дал термодинамический
вывод уравнения Липпмана. В дальнейшем этот вопрос
многократно обсуждался при исследовании электрокапиллярных явлений (см.,
например, [33 –35]). Строгий вывод
уравнения адсорбции Гиббса для плоского поверхностного слоя электрода был дан Парсонсом [36]. Соответствующую теорию для искривленного
слояможно найти в [25, 14]. К весьма сложным разделам термодинамики поверхностных
явлений относится анализ искривленных поверхностей во внешних полях. Гиббсом
было начато рассмотрение поверхностных явлений в гравитационном поле. Что
касается электрического поля, то результаты были получены значительно позднее.
Трудность рассмотрения здесь сильно зависит от того, являются ли соприкасающиеся
фазы проводниками или диэлектриками, Задача для соприкасающихся проводников решается
сравнительно просто [37], для диэлектриков — значительно сложнее [38]. Важным моментом в развитии термодинамики поверхностных
явлений было обобщение уравнения адсорбции Гиббса на случай отсутствия адсорбционного
равновесия. Здесь нужно отметить прежде всего работы Дефэя [39, 40], в которых было введено понятие вторичных
химических потенциалов eiотражающих зависимость поверхностного
натяжения от состояния объемных фаз aи
b: В уравнении (43)
предполагается, что термическое и механическое равновесие установилось, а
диффузионное еще не достигнуто. Процесс установления адсорбционного равновесия включает
трансляционное и вращательное движение молекул, в частности, ориентацию
несферических молекул в поверхностном слое. Если ориентация происходит гораздо
медленнее трансляционно-диффузионного процесса, то можно представить случай,
когда вся неравновесность системы обусловлена процессом
ориентации молекул (например, диполей) в поверхностном слое. Для такого случая
было предложено обобщение уравнения Гиббса [37] где
Следует отметить, что в основе вывода уравнения (44) лежит весьма условное предположение о
независимости трансляционных и вращательных составляющих адсорбционно-диффузионного
процесса. Гиббс в теории капиллярности ограничился рассмотрением
только толстых пленок, в которых можно пренебречь взаимовлиянием поверхностных
слоев на противоположных сторонах пленки. Тонкая пленка принципиально отличается
от толстой тем что ее поверхностные слои нельзя рассматривать независимо друг
от друга. Фактически в тонкой пленке уже нельзявыделить объемную фазу и окружающие ее поверхностные слои, а
необходимо рассматривать пленку в целом. Важной характеристикой, отличающей
тонкую пленку от толстой, является расклинивающее давление; в опытах оно проявляется
в том, что при переходе от толстой к тонкой пленке требуется изменение внешнего
давления. Понятие расклинивающего давления было введено Дерягиным [42], которому принадлежат и первые измерения
этой величины. Существует несколько эквивалентных определений расклинивающего
давления плоской тонкой пленки. Прежде всего расклинивающее давление П можно
определить какразность между
значениями внешнего давления Paна тонкую и
толстую пленку где h — толщина тонкой пленки. Если тонкая пленка образовалась из фазы g
и продолжает находиться с ней в равновесии (например, при прилипании пузырька
к твердой поверхности: фаза a
— газ, фаза g — жидкость), то
расклинивающее давление можно определить как: Наконец, поскольку для плоской пленки внешнее давление
всегда равно нормальной составляющей тензора давления внутри пленки, можно
дать определение и сформулировать его следующим
образом: расклинивающее давление есть разность между нормальным
давлением внутри пленки (или внешним давлением) и давлением в объемной фазе
той же природы при тех же значениях температуры и химических потенциалов, что и
в пленке. Определение (46)
впервые использовали в экспериментальных исследованиях расклинивающего
давления [42 – 45], а определение (47) — для расчетов [46]. Как величина термодинамическая, расклинивающее давление
может быть связано с другими термодинамическими параметрами, и относящиеся к
этой области соотношения образуют термодинамику тонких пленок как особый
раздел теории капиллярности. Разработка этого раздела содержится в целом ряде
работ (см., например, [47 – 57]). Последовательное
изложение термодинамики тонких пленок дано в монографии [25, стр. 259 – 310]. Термодинамика тонких пленок нашла важное
приложение в теориях электрокапиллярности, адсорбциии
хроматографии (ссылки на конкретные работы можно найти в [14]). Здесь мы продемонстрируем в качестве примера подход к
термодинамике тонких пленок, связанный с введением двух разделяющих
поверхностей. Представим, что пленка образовалась путем утоньшения
слоя фазы g между фазами aиb . Тогда, выбрав положение двух разделяющих поверхностей и
взяв избытки со стороны фаз aи
b, мы придем к уравнению (32) для слоя конечной толщины, которое в
данном случае имеет вид где
g — натяжение
пленки;
h — расстояние между разделяющими поверхностями. Теперь мы сделаем еще один шаг [66]: возьмем избыток по отношению к фазеg, то есть вычтем из (48) уравнение Используя определение (53),
получаем где Уравнение (50)
справедливо при любом положении разделяющих поверхностей. Оно играет роль
основного фундаментального уравнения тонкой пленки, из которого могут быть
получены многие другие термодинамические соотношения. В частности, из (50) получаем выражение которое также может рассматриваться
как определение расклинивающего давления. Из
(50) следует еще два фундаментальных уравнения: Уравнение (53)
является аналогом уравнения адсорбции Гиббса (в терминах абсолютной
адсорбции). Как и уравнение адсорбции Гиббса, оно не является самостоятельным
термодинамическим соотношением и для получения каких-либо физических зависимостей
должно рассматриваться совместно с фундаментальными уравнениями для объемных
фаз. Отметим, что приведенные определения расклинивающего
давления относятся только к плоской пленке. При переходе к случаю искривленной
пленки возникают следующие осложнения:определения (45) – (47) перестают быть эквивалентными;
каждое из этих определений утрачивает свою однозначность. Так, если
пользоваться определениями (45) и (46), то для искривленной пленки будут
существовать два расклинивающих давления, поскольку давления Рa
и Рb
по обеим сторонам пленки будут различными. Определением (47) воспользоваться еще труднее, так как в случае искривленной
пленки величина Рn является функцией пространственных координат. Для описания дальнодействующих поверхностных сил в
искривленных пленках можно использовать более фундаментальное понятие работы
смачивания, введенное в [58].
Для плоских пленок работа смачивания просто выражается, если известна
изотерма расклинивающего давления (т.е. зависимость P(h)при данной температуре). Для
искривленных же пленок необходимо делать какие-то другие предположения о виде
зависимости работы смачивания от толщины пленки. Таким образом, даже задача адекватного описания
дальнодействующих поверхностных сил на сегодняшний день остается нерешенной. В целом можно отметить, что термодинамический подход Гиббса
к описанию капиллярности оказался очень плодотворным. По сей день теория
Гиббса остается весьма полезной как в чисто теоретических исследованиях, так и
в прикладных задачах. Значительные успехи достигнуты также в термодинамике
адсорбции, смачивания, нуклеации, электродных процессов
и в других областях. Как видно из приведенного исторического обзора, капиллярные
явления изучаются уже почти триста лет. За это время довольно сильно
изменились способы описания капиллярных и поверхностных сил. Однако,
интересно отметить, что практически с самых первых работ по теории капиллярных
явлений, люди совершенно правильно относили их к макроскопическим проявлениям
сил, действующих между частицами в веществе. С развитием представлений об этих
силах менялось и понимание их роли в тех или капиллярных явлениях. Первые оценки радиуса действия межмолекулярных сил были
грубыми и сильно завышенными. Соответственно, первые теории капиллярности были
грубыми механистическими теориями среднего поля. Теория Гиббса дала совершенно новый инструмент исследования
поверхностных явлений. С использованием мощного и универсального аппарата термодинамики
удалось дать более строгие определения понятиям границы раздела фаз, толщины
пленки и т.д. Кроме того, формула Лапласа для разности давлений в фазах вблизи
искривленной поверхности их раздела была получена в теории Гиббса без всяких
дополнительных предположений о радиусе действия межмолекулярных сил. Подход,
развитый Гиббсом, и сегодня не теряет своей актуальности в силу своей
универсальности и удивительной широты охвата явлений. В настоящеевремя
исследования в области капиллярных и поверхностных сил продолжаются, что
обусловлено как их важностью в различных областях науки, так и широким спектром
практических приложений. 1.
[D&L2]© Hauksbee F.
Physico-Mechanical Experiments, London, 1709, pp. 139–169; and Phil. Trans.,
1711 and 1712. 2.
Maxwell J.C.
Capillary Action. The Encyclopaedia Britannica, 11th edition, Cambrige: at the
University Press, 1910, vol. 5, p. 256. 3.
©
Jurin J. Phil. Trans., 1718, p. 739, and 1719, p. 1083. 4.
© Clairault A.C.
Thйorie de la figure de la terre, Paris, 1808, pp. 105, 128. 5.
© von Segner J.A.
Comment. Soc. Reg. Gцtting. i. (1751), p. 301. 6.
© Leslie J.
Phil. Mag., 1802, vol. xiv p. 193. 7.
© Young T.
Cohesion of Fluids, Phil. Trans., 1805, p. 65. 8.
¨ Laplace P.S. Traitй de Mйcanique
Cйleste; Supplйment au dixiйme livre, Sur l’Action. Capillaire (1807); in:
Oeuvres complйtes de Laplace, v. 4. Gauthiers-Villars, Paris, 1880, p. 349,
419. 9.Роулинсон Дж., Уидом Б.
Молекулярная теория капиллярности. М.: Мир, 1986. 10.¨ Lord Rayleigh, Phil. Mag. 30, 285, 456 (1890); Scentific Papers, v. 3. Cambrige
University Press, 1902, p. 397. 11.¨ Duprй A. Thйorie mйcanique de la Chaleur. Gauthier-Villars,
Paris, 1869, p. 152. § Gibbs J.W.[1] Хоксби был демонстратором в Королевском обществе, и его
опыты повлияли на содержание весьма пространного сочинения о первичных частицах
вещества и силах между ними, которым Ньютон завершил издание своей «Оптики»
1717 года. см. [2] К
1819 г. он был занят детальным обсуждением межмолекулярных сил отталкивания,
которые, хотя и приписывались еще теплоте или теплороду, обладали существенным
свойством уменьшаться с расстоянием быстрее, чем силы притяжения. [3] Юнг
упоминал наличие градиента плотности в конечном по толщине слое, но отбросил
этот эффект, посчитав его несущественным. © Ссылка
приведена по [2]. ¨ Ссылка
приведена по [9]. § Ссылка
приведена по [14]. (16)
(16) (17)
(17) (18)
(18) (19)
(19) (20)
(20) ((7) и (11)), где
постоянная a дается выражением
((7) и (11)), где
постоянная a дается выражением (21)
(21)Теория капиллярности Гиббса.

 — плотность количества молекул сорта j в [объемной]
фазе {l}.
Тогда полное число молекул сорта j в рассматриваемой системе равно
— плотность количества молекул сорта j в [объемной]
фазе {l}.
Тогда полное число молекул сорта j в рассматриваемой системе равно
 — поверхностный избыток количества
молекул сорта j
(индекс {s}
означает surface- поверхность).
Аналогичным образом определяются избытки других экстенсивных физических
величин. Очевидно, что в случае, например, плоской пленки
— поверхностный избыток количества
молекул сорта j
(индекс {s}
означает surface- поверхность).
Аналогичным образом определяются избытки других экстенсивных физических
величин. Очевидно, что в случае, например, плоской пленки пропорционален ее площади
A.Величина,
определяемая как поверхностный избыток числа молекул сорта jна единицу площади разделяющей
поверхности, называется адсорбцией молекул сорта jна этой поверхности.
пропорционален ее площади
A.Величина,
определяемая как поверхностный избыток числа молекул сорта jна единицу площади разделяющей
поверхности, называется адсорбцией молекул сорта jна этой поверхности. (22)
(22) (24)
(24) 
 (25)
(25) [19, стр. 61]
[19, стр. 61] (27)
(27) (28)
(28)Развитие и обобщение теории капиллярности Гиббса.
Метод слоя конечной толщины
 (29)
(29) (30)
(30) (31)
(31) (32)
(32) (33)
(33) —
реальное количество i-го компонента в
слое толщиной t;
—
реальное количество i-го компонента в
слое толщиной t; — абсолютная адсорбция i-го компонента со стороны
фазы a,
отнесенная к разделяющей поверхности со стороны той же фазы;
— абсолютная адсорбция i-го компонента со стороны
фазы a,
отнесенная к разделяющей поверхности со стороны той же фазы; — аналогичная величина адсорбции со
стороны фазы b.
— аналогичная величина адсорбции со
стороны фазы b.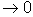 уравнение (32)
переходит в фундаментальное уравнение Гиббса
(25) при t
уравнение (32)
переходит в фундаментальное уравнение Гиббса
(25) при t уравнение (32)
переходит в уравнение (29) для двухфазной системы в целом.
уравнение (32)
переходит в уравнение (29) для двухфазной системы в целом.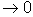 , и отсюда получается
вся теория капиллярности Гиббса, а при t
, и отсюда получается
вся теория капиллярности Гиббса, а при t —другой предельный
вариант термодинамики поверхностных явлений (этот вариант был недавно
рассмотрен Гудричем
[26, стр. 1—37] ), в котором
вообще не используется представление о разделяющей поверхности. Таким
образом, мы можем сказать, что метод слоя конечной толщины является
обобщением метода Гиббса и наиболее общим методом рассмотрения термодинамики поверхностных
явлений.
—другой предельный
вариант термодинамики поверхностных явлений (этот вариант был недавно
рассмотрен Гудричем
[26, стр. 1—37] ), в котором
вообще не используется представление о разделяющей поверхности. Таким
образом, мы можем сказать, что метод слоя конечной толщины является
обобщением метода Гиббса и наиболее общим методом рассмотрения термодинамики поверхностных
явлений.Уравнение адсорбции Гиббса
 (34)
(34) — избыточная
энтропия на единицу поверхности;
— избыточная
энтропия на единицу поверхности; (35)
(35) (36)
(36) (37)
(37) (38)
(38)
 (39)
(39) — тензор избыточных поверхностных
напряжений;
— тензор избыточных поверхностных
напряжений; — единичный
тензор;
— единичный
тензор; тензор поверхностной деформации; символ : означает скалярное произведение тензоров.
тензор поверхностной деформации; символ : означает скалярное произведение тензоров. к мысленной
поверхности разреза.
к мысленной
поверхности разреза. на межфазной
поверхности можно определить величину
на межфазной
поверхности можно определить величину (40)
(40)
 (41)
(41) .
. :
: (42)
(42) и уравнения (39)
и (42) переходят в уравнение адсорбции
Гиббса.
и уравнения (39)
и (42) переходят в уравнение адсорбции
Гиббса. (43)
(43) (44)
(44) — среднее
значение составляющей по оси x дипольного момента молекул
i‑го компонента в фазе
a;
— среднее
значение составляющей по оси x дипольного момента молекул
i‑го компонента в фазе
a; среднее значение квадрата той же величины;
среднее значение квадрата той же величины; и
и  — соответствующие
сродства; суммирование по x иaозначает суммирование по всем
составляющим дипольного момента и по всем фазам и тонким элементарным слоям
внутри поверхностного слоя, рассматриваемым как однородные области.
— соответствующие
сродства; суммирование по x иaозначает суммирование по всем
составляющим дипольного момента и по всем фазам и тонким элементарным слоям
внутри поверхностного слоя, рассматриваемым как однородные области.Развитие новых направлений в
термодинамике поверхностных явлений
Термодинамика тонких пленок
 (45)
(45) (46)
(46) (47)
(47) gdA
gdA (48)
(48) (49)
(49) gdA
gdA (50)
(50) ,
,  и
и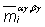 —
совместные для обеих поверхностей избытки энергии, энтропии и массы i-го
компонента.
—
совместные для обеих поверхностей избытки энергии, энтропии и массы i-го
компонента. (51)
(51) gA
gA (52)
(52) (53)
(53)Заключение
Литература.
[D&L1]