Расчёт статически неопределимой балки

Разделы	Технология
Тип	Работа
Формат	Microsoft Word
Язык	Украинский
Примечание	from lav_ua [lav_ua@yahoo.com]
	Загрузить архив:
	Файл: ref-7550.zip (42kb [zip], Скачиваний: 57) скачать

Задача №3.

Розкрити статичну невизначуваність балки. Побудувати епюри Qs, Ms. Підібрати двотавровий переріз та зробити повну первірку міцності балки , якщо [σ]=160 МПа, [τ]=100 МПа.

Розв’язання.

1. Визначаємо ступінь статичної невизначуваності балки (мал. а):

n=4-2=2    рази стат. невизн.

2. Вибираємо основну систему (мал. б).

3. Будуємо еквівалентну систему (мал. в).

4. Записуємо канонічну систему рівнянь методом сил:

        (*)

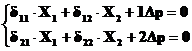5.а). будуємо вантажний стан (мал. г) і епюри Qр (мал. д) та Мр (мал. е).

БалкаАD:

БалкаDF:

    б.) Будуємо одиничні допоміжні стани М₁ (мал. є)і М₂ (мал. ж), а також їх епюри.

     в). Визначаємо Δίр та δίј для (*):

6. Підставляємо отримані значення всистему (*):

Із першого рівняння знаходимо Х₁:

7. За принципом незалежності дії сил будуємо епюру результативних згинальних моментів Ms (мал. з).

№ пер.	Мр	М1 Х1	М2 Х2	Ms=Mp+ М1 Х1+ М2 Х2
1	0	0	0	0
				-33,75
2	-67,5	0	0	-67,5
3	-67,5	0	0	-67,5
				88,594
4	-129,375	0	0	-129,375
5	-129,375	0	0	-129,375
				41,245
6	0	-103,1	0	-103,1
7	0	-103,1	0	-103,1
				5,157
8	118,25	-77,325	-6,1875	34,73
9	118,25	-77,325	-6,1875	34,73
				4,95
10	0	0	-24,75	-24,75

8. Виконуємо деформаційну первірку. Для цього будуємо вантажний стан (мал. )і епюру для нього.

Обчислимо похибку:

9. Методом вирізання ділянок визначаємо поперечні сили Qs і будуємо їх епюру (мал. к):

                                    Р=15 кН

                  0         АВ          67,5

                                    Qs₁Qs2

                       

                      

                                        Qs₃

                                         q=35 (кН/м)

              67,5                                                       129,375

                                   B                      C

                                                 Qs₄

                     

                     

                                        Qs₅

                                         q=35 (кН/м)

        129,375                                                       103,1

                                   C                      D

                                                 Qs₆

                    

                     

                                        Qs₇

                                         q=35 (кН/м)

           103,1                                                         34,73

                                  D                      E

                                                 Qs₈

                     

                    

                       Qs₉

                                    Р=15 кН

             34,73         D                              F          24,75

                                                     Qs₁₀

                       

                      

10. Із умови міцності за нормальними напруженнями знаходимо осьовий момент опору відносно нейтральної лінії Z:

11. Підбираємо двотавровий переріз рами для якого має бути W_Z=808,59 см³. За таблицями сортамента знаходимо що міцним є двотавр №40, для якого W_Z^табл.=953 см³.

Двотавр №40: W_Z^табл.=953 см³, h=400 мм, b=155 мм, d=8,3 мм, t=13 мм.

12. Перевіряємо міцність балки за дотичними напруженнями.