Лабораторные работы по экономико-математическому моделированию
| Загрузить архив: | |
| Файл: laba.zip (118kb [zip], Скачиваний: 54) скачать |
ЛАБОРАТОРНАЯ РАБОТА №1
Системы уравнений межотраслевого баланса.
Вариант №21
Цели:
Выработать у студентов навыки построения математических моделей межотраслевого баланса в статистических случаях и оптимизации моделей в рамках межотраслевого баланса. Научиться делать выводы в рамках построения моделей.
Задание:
1)
2)U-ой
и 
3)
отрасль не может
увеличить объемы выпуска своей продукции более чем на 2 единицы.
4)
Исходные данные:
 |
 |
|
A = |
0.02 0.01 0.01 0.05 0.06 |
0.03 0.05 0.02 0.01 0.01 |
0.09 0.06 0.04 0.08 0.05 |
0.06 0.06 0.05 0.04 0.05 |
0.06 0.04 0.08 0.03 0.05 |
C = |
235 194 167 209 208 |
||
0) Проверим матрицу А на продуктивность:
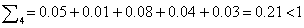
Матрица А является продуктивной матрицей.
1)J-A)
= 
J – единичная матрица;
A – заданная матрица прямых затрат;
- вектор (план)
выпуска продукции, подлежащей определению;
- вектор конечного спроса.
Произведем расчеты на PС, используя метод Гаусса.
; 
;
;
;
Используя Симплекс-метод, получим:
|
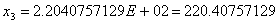
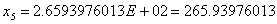
2)
;
;
|
Решение:
3) Скорректировать
новый план, с учетом того, что отрасль не может
увеличить объем выпуска своей продукции, более чем на 2 единицы.
Подставляя значение 
в исходную систему
уравнений, получим:
Решаем систему уравнений методом Гаусса:
4) Рассчитаем матрицу полных затрат.
Произведем обращение матрицы:
Матрица, вычисленная вручную:
Вывод: Видно, что несмотря на сходство этих матриц, полученные приближенные значения довольно грубы.
Рассчитаем деревья матрицы:
|
#1 |
|
1 |
|
0.02 |
|
0.01 |
|
0.05 |
|
0.01 |
|
0.06 |
|
1 2 3 4 5 |
|
0.0004 0.0002 0.0002 0.001 0.0012 |
|
0.0003 0.0005 0.0002 0.0001 0.0001 |
|
0.0018 0.003 0.0012 0.0006 0.0006 |
|
0.0015 0.0025 0.001 0.0005 0.0005 |
|
0.0003 0.0005 0.0002 0.0001 0.0001 |
|
1 2 3 4 5 1 23 4 5 1 2 3 4 5 1 23 4 5 12 3 4 5 |
|
b11 b21 b31 b41 b51 |
|
#2 |
|
1 |
|
0.03 |
|
0.05 |
|
0.01 |
|
0.02 |
|
0.01 |
|
1 2 3 4 5 |
|
0.0006 0.0003 0.0001 0.0015 0.0018 |
|
0.0010 0.0005 0.0005 0.0025 0.0030 |
|
0.0002 0.0001 0.0001 0.0005 0.0006 |
|
0.0002 0.0001 0.0001 0.0005 0.0006 |
|
0.0004 0.0002 0.0002 0.0010 0.0012 |
|
1 2 3 4 5 1 23 4 5 1 2 3 4 5 1 23 4 5 1 2 3 4 5 |
|
b12 b22 b32 b42 b52 |
|
#3 |
|
1 |
|
0.09 |
|
0.06 |
|
0.08 |
|
0.04 |
|
0.05 |
|
1 2 3 4 5 |
|
0.0018 0.0009 0.0009 0.0045 0.0054 |
|
0.0027 0.004 0.0018 0.0009 0.0009 |
|
0.0054 0.0036 0.0072 0.0027 0.0045 |
|
0.0054 0.0054 0.004 0.0036 0.004 |
|
0.0081 0.0054 0.0036 0.0072 0.004 |
|
1 2 3 4 5 1 23 4 5 1 2 3 4 5 1 23 4 5 12 3 4 5 |
|
b13 b23 b33 b43 b53 |
|
#4 |
|
1 |
|
0.06 |
|
0.06 |
|
0.04 |
|
0.05 |
|
0.05 |
|
1 2 3 4 5 |
|
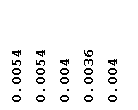
0.0012 0.0006 0.0006 0.003 0.0036 |
|
0.0018 0.0030 0.0012 0.0006 0.0006 |
|
0.0036 0.0024 0.0048 0.0018 0.003 |
|
0.0036 0.0036 0.003 0.0024 0.003 |
|
0.0054 0.0036 0.0024 0.0048 0.003 |
|
1 2 3 4 5 1 23 4 5 1 2 3 4 5 1 23 4 5 1 2 3 4 5 |
|
b14 b24 b34 b44 b54 |
|
#5 |
|
1 |
|
0.06 |
|
0.04 |
|
0.03 |
|
0.08 |
|
0.05 |
|
1 2 3 4 5 |
|
0.0012 0.0006 0.0006 0.003 0.0036 |
|
0.0018 0.0030 0.0012 0.0006 0.0006 |
|
0.0036 0.0024 0.0048 0.0018 0.003 |
|
0.0036 0.0036 0.003 0.0024 0.003 |
|
0.0054 0.0036 0.0024 0.0048 0.003 |
|
1 2 3 4 5 1 23 4 5 1 2 3 4 5 1 23 4 5 1 2 3 4 5 |
|
b15 b25 b35 b45 b55 |
ЛАБОРАТОРНАЯ РАБОТА №2
Оптимизационная модель межотраслевого баланса.
Зная запасы дополнительных ресурсов (r), нормы их затрат (D) на производство продукции каждой отрасли и цены реализации конечной продукции (p), рассчитать объемы производства продукции, обеспечивающие максимальный фонд конечного спроса. Вычислить конечный спрос и провести анализ полученного решения:
1);
2);
3)
Рассчитать объем производства.
Исходные данные:
 |
|
D = |
0.3 0.6 0.5 |
0.6 0.6 0.9 |
0.5 0.8 0.1 |
0.9 0.4 0.8 |
1.1 0.2 0.7 |
298 467 |
= 564
Требуется максимизировать цену конечного спроса;
=
, при ограничениях:
 |
|
Решим соответствующую двойственную задачу:
Решая задачу на ЭВМ, симплекс-методом, получим:
Проведем анализ результатов:
1) Оптимальность:
|
Оптовая цена конечного спроса: 
т.е. С1=336.67, С2=-26.1275, С3=353.8225, С4=-48.6875, С5=-41.29,
отрицательные значения говорят о том, что продукция отраслей необходимая для функционирования.
2) Статус и ценность ресурсов:
|
Ресурс |
Остаточная переменная |
Статус ресурса |
Теневая цена |
|
1 |
x6 = 21,67 |
недефицитный |
0 |
|
2 |
X7 = 88,96 |
недефицитный |
0 |
|
3 |
X8 = 0,26 |
недефицитный |
0 |