Высшая математика (шпаргалка)
| Загрузить архив: | |
| Файл: ref-10032.zip (499kb [zip], Скачиваний: 409) скачать |
1. Векторы. Действия над векторами.
Вектором наз. упорядоченная совокупность чисел Х={X1,X2,...Xn} вектор дан в n-мерном пространстве. Т(X1,X2,X3). n=1,2,3. Геометрический вектор - направленный отрезок. |AB|=|a| - длинна. 2 вектора наз. коллинеарными, если они лежат на 1 прямой или ||-ных прямых. Векторы наз. компланарными, если они лежат в 1-ой плоскости или в ||-ных плоскостях. 2 вектора равны, когда они коллинеарны, сонаправленны, и имеют одинак-ую длинну.
1.умножение на число: произведение вектора А на число l наз. такой вектор В, который обладает след. св-ми: а) А||В. б) l>0, то АВ, l<0, то А¯В. в)l>1, то А<В, )l<1, то А>В. 2. Разделить вектор на число n значит умножить его на число, обратное n: а/n=a*(1/n).
3.Суммой неск-их
векторов а и в наз. соединяющий начало 1-го и конец последнего
вектора. 4. Разностью векторов а и в наз-ся вектор c, который, будучи сложенным с вектором в даст вектор
а.
2.3. Декартова прямоугольная система координат. Базис.
Базисом на плоскости называется совокупность фиксированной точки и 2х неколлинеарных векторов, проведенных к ней.
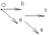Базисом в пространстве
наз. совокупность фиксированной точки в пространстве и 3х некомпланарных
векторов.
Любой вектор на
плоскости может быть разложен по векторам базиса на плоскости. Любой вектор в
пространстве может быть разложен по векторам базиса в пространстве.
ОС=OA+OB, OA=x*i, OB=j*y, OC=xi+yj.
Числа х,у
наз-ся координатами вектора ОС в данном базисе
4. Действия над векторами.
а=х1i+y1j+z1k; b=х2i+y2j+z2k
l*a=l(х1i+y1j+z1k)= l(х1)i+l (y1)j+l(z1)k
a±b=(x1±x2)i+(y1±y2)j+(z1±z2)k
ab=x1x2ii+y1x2ij+x2z1ki+x1y2ij+y1y2jj+ z1y2kj+x1z1ik+y1z2jk+z1z2kk=x1x2+y1y2+z1z2
ii=1; ij=0; и т.д.
скалярное произведение 2х векторов равно сумме произведений соответствующих координат этих векторов.
аа=x2+y2+z2=|a|2 a{x,y,z}, aa=|a|*|a|, то a2=|a|2
ab=|a|*|b|*cosj
а)ав=0,<=>а^в, x1x2+y1y2+z1z2=0
б)а||в - коллинеарны, если , x1/x2=y1/y2=z1/z2
5. Скалярное произведение векторов и его свойства.
-(“skala”-шкала) 2х векторов а и в наз. число, равное произведению длин этих векторов на cos угла между ними. (а,в)- скалярное произведение. а*в=|а|*|в|*cosj, j=p/2, cosp/2=0, a^b=>ab=0. Равенство “0” скаляргного произведения необходимое и достаточное условие их перпендикулярности (ортогональности).
6. Векторное произведение 2х векторов.
левая ----- правая
Тройка векторов а,в,с наз. правоориентированной (правой), если с конца 3го вектора с кратчайший поворот от 1го ко 2му вектору мы будем видеть против час. стрелки. Если кратчайший поворот от 1го ко 2му по час. стрелки - левая. Векторным произведением 2х векторов а и в наз. такой вектор с, который удовлетворяет условиям: 1. |c|=|a|*|b|*sinj. 2. c^aи c^b. 3. тройка а,в,с-правая.
7. Смешанное произведение векторов и его свойства.
Смешанным произведением векторов наз. векторно-скалярное произведение, являющееся числом: a*b*c=[a*b]*c=a*[b*c], где
a={ax,ay,az}
b={bx,by,bz}
c={cx,cy,cz}
Св-ва:
1. При перестановке 2х сомножителей:
a*b*c=-b*c*a
2. не меняется при перестановке циклических сомножителей:
a*b*c=c*a*b=b*c*a
3.а)(Геометрич. смысл) необходимым и достаточным условием компланарности 3х векторов явл. равенство a*b*c=0
б)если некомпланарные вектора a,b,c привести к 1 началу, то |a*b*c|=Vпараллепипеда, построенного на этих векторах
если a*b*c>0, то тройка a,b,c - правая
если a*b*c<0, то тройка a,b,c - левая
8. Уравнение линии и поверхности.
1. Уравнение сферы. Сфера- геометрическое место точек, равноудаленных от 1ой точки, называемой центром.
O(a,b,c)
|OM|=r, OM={x-a,y-b,z-c}
r2=(x-a)2+(y-b)2+(z-c)2- уравнение сферы. x2+y2+z2=r2- ур-е сферы с центром точке(0,0).
F(x,y,z)=0- ур-е поверхности - ур-ю, удовлетворяющему координатам x,y,z любой точки, лежащей на поверхности.
2. Уравнение окружности
|OM|=r, OM={x-a,y-b)
r2=(x-a)2+(y-b)2+(z-c)2- ур-е окружности
а=b=0, то x2+y2=r2
F(x,y)=0- ур-е линии на плоскости.
9. Плоскость в пространстве.
Ур-е в плоскости, проходящей через данную точку, перпендикулярно заданному вектору.
N-вектор
нормали
M0M{x-x0,y-y0,z-z0}
Для того, чтобы точка MÎP, необходимо и достаточно чтобы вектора N^M0M(т.е. N*M0M=0)
A(x-x0)+B(y-y0)+С(z-z0)=0 - ур-е плоскости, проходящей через данную точку ^вектору.
10. Общее уравнение плоскости.
Ax+By+Сz-Ax0-By0-Сz0=0
-Ax0-By0-Сz0=D, где D=Ax+By+Сz
Ax+By+Сz+D=0
Частный случай:
Если D=0, то Ax+By+Сz=0(проходит ч/з 0;0)
Если A=0, то By+Сz+D=0
Если B=0, то Ax +Сz+D=0
Если C=0, то Ax+By+D=0
Если A=B=0, то Сz+D=0
Если A=C=0, то By+D=0
Если A=D=0, то By+Сz=0
Если B=D=0, то Ay+Сz=0
11. Взаимное расположение плоскостей.
N1,N2-нормальные векторы плоскости.
P:A1x+B1y+C1z+D1=0
Q:A2x+B2y+C2z+D2=0
P^Q{A1,B1,C1}
Q^N2{A2,B2,C2}
1)Пусть P^Q<=>N1^N2
A1A2+B1B2+C1C2=0 условие перпендикулярности P^Q.
2) Пусть P^Q<=> N1^N2
A1/A2=B1/B2=C1/C2- Условие параллельности 2х плоскостей.
A1/A2=B1/B2=C1/C2=D1/D2- Условие совпадения 2х плоскостей.
12. Каноническое уравнение прямой в пространстве.
M0M{x-x0,y-y0,z-z0}
Чтобы точка МÎпрямой(или лежала на ней) необх. и достаточно, чтобы M0M||S
13. Уравнение прямой в пространстве, проходящей ч/з 2 заданные точки.
l m n
S{x2-x1,y2-y1,z2-z1}
14. прямая, как пересечение плоскостей. Нахождение начальной точки и направляющего вектора прямой.
P:A1x+B1y+C1z+D1=0
Q:A2x+B2y+C2z+D2=0
Общее ур-е прямой в пространстве.
Для того, чтобы перейти от общего к каноническому ур-ю прямой, надо задать начальную точку и направляющий вектор:
1. Найдем начальную точку:
Z=0 
M0(x0,y0,0), т.к. Z=0
2. Найдем направляющий вектор S-?
P^N1{A1,B1,C1}
Q^N1{A2,B2,C2}
S=N1*N2
16. Взаимное расположение прямой на плоскости.
P:A1x+B1y+C1z+D1=0^N1{A1,B1}
Q:A2x+B2y+C2z+D2=0^N2{A2,B2}
а)
то 
б)
q<=> N1||N2, то A1/A2=B1/B2
в)
N1^N2, то A1A2+B1B2=0
17. Общее
ур-е прямой линии на плоскости. Его частные случаи.
Сначала запишем ур-е прямой, проходящей через заданную точку ^ заданному вектору.
M0(x0,y0)
M0M{x-x0,y-y0}
n*M0M=0
A(x-x0)+B(y-y0)=0
Ax+By-Ax0-By0=0
-Ax0-By0=C
Ax+By+C=0-общее уравнение прямой на плоскости.
18.19. Каноническое ур-е прямой линии на плоскости. Ур-е прямой, проходящей ч/з 2 точки. Ур-е с угловым коэффициентом.
y-y1=k1(x-x1)
y=k1x-k1x1+y1
y1-k1x1=b
y=k1x+b
ур-е прямой с угловым коэффициентом k.
Пусть даны 2 точки M1(x1,y1),
M2(x2,y2) и x1¹x2, y1¹y2. Для составления
уравнения прямой М1М2 запишем уравнения пучка прямых,
проходящих через точку М1: y-y1=k(x-x1).
Т.к. М2лежит
на данной прямой, то чтобы выделить ее из пучка, подставим координаты точки М2
в уравнение пучка М1: y-y1=k(x-x1)
и найдем
k:
Теперь вид искомой прямой имеет вид:
- Ур-е прямой, проходящей ч/з 2
20,21.
Угол м/ду прямыми на плоскости. Условия ||
и^.
а) 
S1{l1,m1} S2{l2,m2},
или
p:y=k1x+b1, k1=tgj1
q:y=k2x+b2, k2=tgj2 =>tgj=tg(j2-j1)=
=(tgj2-tgj1)/(1+ tgj1tgj2)=
=(k2-k1)/(1+k1k2).
б) p||q, tgj=0, k1=k2
в)p^q,то
22. Расстояние от точки до прямой на плоскости и до плоскости в пространстве.
1. Ax+By+C=0, M0(x0,y0)
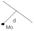
2. Пусть плоскость задана ур-ем Ax+By+Cz+D=0
23. Кривые линии 2-го порядка.
Кривые 2го порядка описываются с помощью общего ур-я:
Ax2+2Bxy+Cy2+2Dx+2Ey+F=0, где
а) Каноническое ур-е эллипса
- Каноническое ур-е
эллипса
Если a=b, то x2+b2=a2 - ур-е окружности.
б) Ур-е гиперболы: x2/a2-y2/b2=1
в) ур-е параболы: y2=2px или y=ax2
г) ур-е сферы: x2+y2+z2=а2 (r2=(x-a)2+(y-b)2+(z-c)2)
д) ур-е эллипса: x2/a2-y2/b2+z2/c2=1
24. Парабола и ее свойства.
Множество точек плоскости, координаты которых по отношению к системе декартовых координат удовлетворяет уравнению y=ax2, где х и у - текущие координаты, а- нек. число, наз. параболой.
Если вершина нах. в
О(0,0), то ур-е примет вид
y2=2px-симметрично отн. оси ОХ
х2=2pу-симметрично отн. оси ОУ
Точка F(p/2,0) наз. фокусом параболы, а прямая x=-p/2 - ее директриса.
Любой точке М(х,у), принадлежащей параболе, расстояние до фокуса = r=p/2
Св-ва:
1. парабола предст. собой ¥ точек плоскости, равноотстающих от фокуса и от директрисы y=ax2.
25.Эллипс и его св-ва:
Кривая второго порядка наз. эллипсом если коэффициенты А и L имеют одинаковые знаки
Аx2+Cy2=d
ур.-е 
наз. канонич. ур.-ем
эллипса, где 
При а=в представляет
собой ур-е окружности х2+y2=а2
Точки F1(-c,0) и F2(c,0) - наз. фокусами эллипса а.
Отношение e=с/а наз. его эксцентриситетом (0<=e<=1)
Точки A1,A2,B1,B2 -вершины эллипса.
Св-во:
Для любой точки эллипса сумма расстояний этой точки до фокусов есть величина
постоянной, =2а.
26. Гипербола и ее св-ва.
Кривая 2го порядка наз. гиперболой, если в ур-ии Ax2+Cy2=d, коэффициент А и С имеют противоположные знаки, т.е. А*С<0
б) Если d>0, то каноническое ур-е гиперболы примет вид: x2/a2-y2/b2=1, F1(c,o) и F2(-c,0) - фокусы ее, e>0, e=c/a - эксцентриситет.
Св-во:
для любой точки гиперболы абсолютная величина разности ее расстояний до фокусов
есть величина постоянная = 2а.
б) если d=0, ур-е примет вид x2/a2-y2/b2=0, получаем 2 перекрестные прямые х/а±у/b=0
в) если d<0, то x2/a2-y2/b2=-1 - ур-е сопряженной гиперболы.
27. Понятие о поверхностях 2го порядка.
Алгебраическим ур-ем 2ой степени наз. ур-е вида Ax2+Bxy+Cy2+Dx+ey+F=0, где A,B,C,D,e,F - действительные числа
Линии, которые в системе декартовых координат определяются алгебраическим ур-ем 2ой степени наз. линиями 2го порядка.
28. Функции. Определение способа задания. Классификация функций. Основные элементарные функции.
Функция - это зависимость одной величины от другой.
Если существует взаимооднозначное соответствие между переменной х одного множества и переменной у другого множества, то она называется функциональной зависимостью. y=f(x).
Определение способа задания:
-аналитически (y=kx+b)
-графический (график)
-таблично
|
x |
1 |
2 |
3 |
|
y |
4 |
5 |
8 |
-алгоритмически (с помощью ЭВМ)
Классификация функций:
Элементарные: - функции, которые получаются из основных элементарных ф-ций с помощью алгебраических действий (+,-,*,/,введение в степень). Основные элементарные ф-ции:
1. y=xn - степенная
2. y=ax - показательная
3. y=logax - логарифмическая
4. y=sinx, y=cosx - тригонометрические.
Сложные:
Y=f(U), где U=j(x), Y=f[j(x)]
Если ф-ция у зависит от промежуточного аргумента U, который зависит от независимой переменной х, то y=f[j(x)] называется сложным заданием х.
29. Определение пределов последовательности и ф-ции. Осн. св-ва пределов ф-ции 1ой переменной.
а) Предел последовательности:
y=f(Un), где U1,U2,...Un, а Un=n/(n2+1)
limxn=a n®¥ -e a-e б)
Предел ф-ции:
Предел: число а
называется пределом переменной xn, если для каждого “+”
как угодно малого числа e(эпсилон) существует такой номер
N, что
при n>N разность |xn-a|
y=f(x) число а называется пределом переменной х, если разность
м/ду ними есть б.м.в. |x-a|®0, |x-a|
j
33. Непрерывность
ф-ции в точке и на интервале.
2. Если ф-ция y=f(x)
непрерывна на [a,b], то она ограничена на этом промежутке.
KN=Dy, MK=Dx
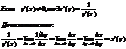
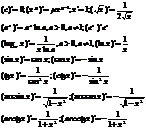
Если функция f(x)
непрерывна на заданном промеж/ [a,b]
деффер. на интервале (a,b)f(a)=f(b)
то существует т. с из интерв. (a,b),
такая, что f’(c)=0.
¥ касательных).
dxZ=Zx`*Dx=¶Z/¶x*dx; dxZ=Zy`*Dy=¶Z/¶y*dy
