Шпаргалки по высшей математике
| Загрузить архив: | |
| Файл: ref-9900.zip (267kb [zip], Скачиваний: 887) скачать |
|
до |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Интегрирование по частям

Простейшие дроби


Для


Интегрирование тригонометрических выражений:
1)

 ;
; 
2)Обе степени четные (sinи cos)


 ;
; 
Одна – нечетная:


 ;
; 
3)


4)Для 

Иррациональные функции (дроби)
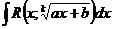






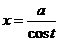




|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ряд – сума  an – общий член ряда.
an – общий член ряда.
Частичная сумма 
Ряд
называется сходящимся, если существует 
Ряд
называется расходящимся, если не существует 
Сходимость/расходимость рядов:
Если
 ряд расходится.
ряд расходится.
Ряды с положительными членами.

|
|
Если сходится (2) Þ сходится (1) Если расходится (1) Þ расходится (2) |
Признак Даламбера
|
|
Ряд сходится Ряд расходится Нужны доп. исследования |
Интегральный признак Коши
|
|
|
Обобщенные гармонические ряды
|
|
Сходится при Расходится при |
Предельная теорема сравнения.
 ряды (1) и (2)
сходятся/расходятся одновременно.
ряды (1) и (2)
сходятся/расходятся одновременно.
Ряды с произвольными членами.
|
|
Если (2) сходятся: (1) – абсолютно сходящийся (2) расход., (1) – сход.: (1) – условно сходящийся |
Теорема об абсолютной сходимости:
Если (2) – сходится, то (1) – тоже сходится (обратное неверно)
|
Знакочередующиеся ряды.
|
Признак Лейбница (только для (*)) (*) сходится, если: 1)
2)
|

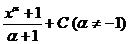








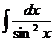





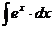









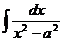








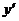








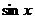






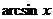















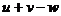


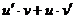





























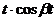























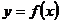 определена при
определена при 
 монотонно убывает
при
монотонно убывает
при 
 (1) и (2) сходятся/расходятся одновременно.
(1) и (2) сходятся/расходятся одновременно.





