Расчетная работа по дисциплине "Информатика" (создание шаблона "Пояснительная записка")


	Загрузить архив:
	Файл: ref-9889.zip (73kb [zip], Скачиваний: 26) скачать

Пояснительная записка

К выполнению расчетной работы

по дисциплине

“информатика”

проверил:

ассистент

фролова т.а

выполнил:

студент группы ТВГ-101

фролов А.В.

СОДЕРЖАНИЕ

Стр.

Введение ………………………………………………………………………….. 3

1 Разработка шаблона для оформления "Пояснительной записки" ………….. 4

1.1 Задание параметров страницы …………………………………………… 4

1.2 Изменение встроенных стилей …………………………………………… 4

1.3 Создание специальных стилей …………………………………………… 6

1.4 Создание колонтитула первой страницы ………………………………... 7

1.5 Создание колонтитула второй и последующих страниц ……………….. 7

1.6 Оформление титульного листа …………………………………………… 8

2 Задача № 1 ………………………………………………………………………. 9

2.1 Теоретический подход к решению задачи ………………………………. 9

2.2 Решение задачи с использованием электронного табличного

процессора Excel …………………………………………………………. 10

2.2.1 Определение вида функции ……………………………………….. 10

2.2.2 Построение графика функции ……………………………………... 11

2.2.3 Редактирование графика функции ………………………………… 12

3 Задача № 2 ………………………………………………………………………. 13

3.1 Теоретический подход к решению задачи ………………………………. 13

3.2 Решение задачи с использованием электронного табличного

процессора Excel …………………………………………………………. 14

Заключение ……………………………………………………………………….. 16

ВВЕДЕНИЕ

Целью данной работы является создание шаблона "Пояснительная записка" и использование его при создании текстового документа, оформляемого в соответствии с требованиями ГОСТ.

Помимо изменения встроенных стилей ("Обычный", "Заголовок 1", "Заголовок 2", "Заголовок 3", "Оглавление 1", "Оглавление 2", "Оглавление 3") шаблон включает специальные стили ("Введение" и "Надпись").

Стиль "Введение" служит для оформления заголовков, по стандарту не требующих нумерации. К таким заголовкам относятся: Введение, Заключение, Список использованной литературы.

Стиль "Надпись" предполагается использовать при оформлении текста, форматирование которого осуществляется по центру без отступа красной строки. Например: заголовок "Содержание", формула без номера, а также любой текст, заключенный в таблицу или надпись.

Работа разделена на три части.

В первой части подробно рассмотрено создание шаблона "Пояснительная записка в соответствии с полученным вариантом задания.

Вторая и третья части представляют собой пошаговое решение задач при помощи электронных таблиц Excel. Результаты вычислений (таблицы и диаграммы) через буфер обмена импортируются в пояснительную записку с последующим изменением атрибутов объекта.

Завершающим этапом явилось оформление титульного листа и вставка содержания.

1

Настоящий шаблон разработан для создания текстовых документов, оформленных в соответствии с требованиями существующих стандартов. Разработка шаблона протекала в несколько этапов:

1.1

1.1.1

1.1.2

Поля: верхнее – 1,5 см, нижнее – 2 см, левое – 2,5 см, правое – 1 см.

От края до верхнего колонтитула – 0,75 см.

Размер бумаги: формат 210´297 мм, ориентация – книжная.

Макет: различать колонтитулы первой страницы.

1.2

В соответствии с выданным вариантом задания изменяем стили, необходимые нам для работы ("Обычный", "Заголовок 1", "Заголовок 2", "Заголовок 3", "Оглавление 1", "Оглавление 2", "Оглавление 3"), а также создаем два новых стиля ("Введение" и "Надпись").

1.2.1

Основан на стиле "Обычный".

Стиль следующего абзаца: "Обычный".

Шрифт: Times New Roman, 12пт, обычный.

Абзац: выравнивание по ширине, уровень – основной текст, отступ слева, справа – 0, отступ красной строки – 1,5 см, интервал перед, после – 0, межстрочный интервал – полуторный.

Положение на странице: запрет висячих строк.

1.2.2

Основан на стиле "Обычный".

Стиль следующего абзаца: "Обычный".

Шрифт: Times New Roman, 12 пт, полужирный.

Абзац: выравнивание по левому краю, уровень – уровень 1, отступ слева, справа – 0, отступ красной строки – 1,5 см, интервал перед – 30 пт, после – 3 пт, межстрочный интервал – полуторный.

Положение на странице: запрет висячих строк, не разрывать абзац, не отрывать от следующего, с новой страницы, запретить автоматический перенос слов.

Нумерация: многоуровневый, уровень – 1, формат номера – "", шрифт: TimesNewRoman, 12 пт, полужирный, положение номера – по левому краю на 1,5 см, нумеровать заново, отступ – 0, символ после номера – пробел.

1.2.3

Основан на стиле "Обычный".

Стиль следующего абзаца: "Обычный".

Шрифт: Times New Roman, 12 пт, полужирный.

Абзац: выравнивание по левому краю, уровень – уровень 2, отступ слева, справа – 0, отступ красной строки – 1,5 см, интервал перед, после – 3 пт, межстрочный интервал – полуторный.

Положение на странице: запрет висячих строк, не разрывать абзац, не отрывать от следующего, запретить автоматический перенос слов.

Нумерация: многоуровневый, уровень – 2, формат номера – " . ", шрифт: TimesNewRoman, 12 пт, полужирный, положение номера – по левому краю на 1,5 см, нумеровать заново, отступ – 0, символ после номера – пробел.

1.2.4

Основан на стиле "Обычный".

Стиль следующего абзаца: "Обычный".

Шрифт: Times New Roman, 12 пт, полужирный.

Абзац: выравнивание по левому краю, уровень – уровень 3, отступ слева, справа – 0, отступ красной строки – 1,5 см, интервал перед, после – 3 пт, межстрочный интервал – полуторный.

Нумерация: многоуровневый, уровень – 2, формат номера – " .. ", шрифт: TimesNewRoman, 12 пт, полужирный, положение номера – по левому краю на 1,5 см, нумеровать заново, отступ – 0, символ после номера – пробел.

1.2.5

Основан на стиле "Обычный".

Стиль следующего абзаца: "Обычный".

Шрифт: Times New Roman, 12 пт, обычный.

Абзац: выравнивание по ширине, уровень – основной текст, отступ слева – 0,75 см, справа – 0, интервал перед, после – 0 пт, межстрочный интервал – полуторный.

Положение на странице: запрет висячих строк, не разрывать абзац.

Табуляция: позиции табуляции – 17,5 см, выравнивание – по правому краю, заполнитель – 2.

1.2.6

Основан на стиле "Обычный".

Стиль следующего абзаца: "Обычный".

Шрифт: Times New Roman, 12 пт, обычный.

Абзац: выравнивание по ширине, уровень – основной текст, отступ слева – 1,25 см, справа – 0, интервал перед, после – 0 пт, межстрочный интервал – полуторный.

Положение на странице: запрет висячих строк.

Табуляция: позиции табуляции – 17,5 см, выравнивание – по правому краю, заполнитель – 2.

1.2.7

Основан на стиле "Обычный".

Стиль следующего абзаца: "Обычный".

Шрифт: Times New Roman, 12 пт, обычный.

Абзац: выравнивание по ширине, уровень – основной текст, отступ слева – 2 см, справа– 0, интервал перед, после – 0 пт, межстрочный интервал – полуторный.

Положение на странице: запрет висячих строк.

Табуляция: позиции табуляции – 17,5 см, выравнивание – по правому краю, заполнитель – 2.

1.3

1.3.1

Основан на стиле "Обычный".

Стиль следующего абзаца: "Обычный".

Шрифт: Times New Roman, 12 пт, полужирный.

Абзац: выравнивание по центру, уровень – уровень 1, отступ слева, справа – 0, интервал перед, после – 6 пт, межстрочный интервал – полуторный.

1.3.2

Основан на стиле "Обычный".

Стиль следующего абзаца: "Надпись".

Шрифт: Times New Roman, 12 пт, обычный.

Абзац: выравнивание по центру, уровень – основной текст, отступ слева, справа – 0, интервал перед, после – 0, межстрочный интервал – полуторный.

Положение на странице: запрет висячих строк.

1.4

1.4.1

Строим в области верхнего колонтитула прямоугольник со следующими параметрами:

Размер: высота – 28 см, ширина – 18,5 см.

Цвета и линии: толщина – 1 пт, заливки нет.

Положение: устанавливаем привязку от страницы, по горизонтали – 2 см, по вертикали– 0,5 см.

Обтекание: нет.

1.4.2

В поле колонтитула создаем надписи с параметрами, приведенными в таблице 1.

Таблица 1

Формат надписи	1-я надпись	2-я надпись
Размер	высота	4 см	1 см
ширина	18 см	17,5 см
Цвета и линии	нет линий, нет заливки
Положение	по горизонтали	установить привязку от страницы
2,25 см	2,5 см
по вертикали	установить привязку от страницы
1,25 см	27 см
Обтекание	нет

1.4.3

Вводим текст, оформленный стилем "Надпись", в надписи, затем изменяем параметры шрифта (размер и начертание).

1.5

1.5.1

Создаем вторую страницу шаблона путем вставки разрыва страницы.

1.5.2

Строим в области верхнего колонтитула прямоугольник с параметрами аналогичными рамке колонтитула первой страницы.

1.5.3

В поле колонтитула вставляем номер страницы вверху и справа (т.е. нумерация страниц будет начинаться со второй страницы пояснительной записки).

1.6

1.6.1

В области основного текста на первой странице создаем надписи с параметрами, приведенными в таблице 2.

Таблица 2

Формат надписи	1-я надпись	2-я надпись	3-я надпись
Размер	высота	5 см	4,5 см	4,5 см
ширина	16 см	6,5 см	6,5 см
Цвета и линии	нет линий, нет заливки
Положение	по горизонтали	установить привязку от страницы
3,5 см	4 см	12 см
по вертикали	установить привязку от страницы
10 см	18 см	18 см
Обтекание	нет

1.6.2

Вводим текст, оформленный стилем "Надпись", в надписи, затем изменяем параметры шрифта (размер и начертание).

1.6.3

Созданный шаблон сохраняем в файл пользователя под именем "Пояснительная записка".

2

Даны координаты трех точек А(-2;4), B(-1;5), C(6;2), Построить квадратную параболу, проходящую через все эти точки.

2.1

Уравнение квадратной параболы имеет вид

y=ax²+bx+c (1)

Для определения неизвестных коэффициентов (a, b, c) запишем систему уравнений, подставив известные значения абсцисс и ординат точек A, B, C.

(2)

В матричном виде уравнение примет вид

[A] ´ C = P (3)

(4)

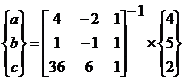
(5)

Excel

2.1.1

1. Вводим значения исходной матрицы [A] в ячейки А1:C3

4	-2	1
1	-1	1
36	6	1

и вектора свободных членов Р в ячейки E1:E3 таблицы Excel.

2. Вычисляем обратную матрицу [A]^-1.

Выделяем область формирования обратной матрицы А5:C7 и в командную строку вводим формулу ее нахождения

= МОБР (А1:C3) (6)

Ввод формулы завершаем одновременным нажатием клавиш [Ctrl]+[Shift]+[Enter]

0,1	-0,1	0
-0,6	0,6	0,1
-0,8	1,7	0

3. Умножаем матрицу [A]^-1 на вектор Р.

Выделяем область формирования вектора неизвестных коэффициентов с E5:E7 и в командную строку вводим формулу перемножения матриц

= МУМНОЖ (А5:С7; D1:D3) (7)

Ввод формулы завершаем одновременным нажатием клавиш [Ctrl]+[Shift]+[Enter]

Получаем вектор неизвестных коэффициентов

E5	-0,2
E6	0,5
E7	5,6

Таким образом, парабола, проходящий через точкиA(-2;4), B(-1;5), C(6;2), имеет вид

y = - 0,2x²+ 0,5x + 5,6 (8)

2.1.2

1. A9:I9

-2

-1

2. Найденная функция (8) вводится в ячейку А10

= -0,2*СТЕПЕНЬ (A9;2)+0,5*A9+5,6 (9)

3. Вводим формулу для определения значения функции для всех значений аргумента в ячейки A10:I10 путем растягивания ячейки А10

5,6

5,9

5,4

4,6

3,5

4. Для упрощения восприятия дальнейшего построения графика функции ограничимся значениями с одним знаком после запятой.

5. Определяем место размещения (ячейка H12) и тип диаграммы (график по точкам без маркеров со сглаженной линией)

6. Для нового ряда исходных данных задается:

Имя: График,

Значения по Х: =: Лист1!$A$9:$I$9,

Значения по Y: = Лист 1!$A$10:$I$10,

Требуемые установки диалогового окна "Параметры диаграммы"

- X и Y – нет,

- X и Y – есть,

- Y пересекается с осью Х в точке с абсциссой 0,

7. Созданную диаграмму через буфер обмена вставляем в пояснительную записку

Рис. 1 График функции, проходящей через заданные точки А (-2;4), B(-1;5), C(6;2) и соответствующий формуле (9).

2.1.3

Изменение диаграммы производятся в Excel.

Имя: Точка 1.

Значение по X: Лист1!$A$9,

Значение по Y: Лист1!$A$10,

Имя: Точка 2.

Значение по X: Лист1!$B$9,

Значение по Y: Лист1!$B$10,

Имя: Точка3.

Значение по X: Лист1!$I$9,

Значение по Y: Лист1!$I$10.

Требуемые установки диалогового окна "Параметры диаграммы" аналогичны ряду исходных данных "График".

Отредактированную диаграмму через буфер обмена вставляем в пояснительную записку

Рис. 2 График функции, проходящей через заданные точки А (-2;4), B(-1;5), C(6;2), с нанесенными маркерами и соответствующий формуле (9).

3

Используя формулы численного интегрирования (прямоугольников "с избытком" и "с недостатком", трапеций, парабол), определить площадь фигуры, ограниченной построенной кривой, осью абсцисс 0Х, и прямыми, проходящими через заданные крайние точки и перпендикулярными оси 0Х. На основании проведенного анализа результатов сделать вывод о предпочтительности применения одной из формул в данном конкретном случае.

3.1

Для решения поставленной задачи необходимо провести интегрирование полученной функции (9) в пределах отрезка [-2;6], ограниченного заданными крайними точками A и C.

C(6;2) и перпендикулярными оси 0Х, равна:

(11)

Тогда точное решение данного интеграла (11) будет равно

(12)

Точная площадь фигуры

S = 37,87 ед²

Для определения площади фигуры с помощью формул численного интегрирования в пределах отрезка (-2; 6) проведем по семи точкам.

(13)

(14

(15

Площадь фигуры по формуле парабол

(16)

где h- шаг интегрирования определяется по формуле

3.2 Excel

1. На том же листе Excel в ячейках A12:G20 создадим таблицу

Таблица 3

	A	B	C	D	E	F	G
12		Площадь	% ошибки
13	Точное решение
14	Формула прямоугольников с "недостатком"
15	Формула прямоугольников с "избытком"
16	Формула трапеций
17	Формула парабол
18
19
20	дает наиболее низкий процент ошибки равный

2. В ячейку F13 вводим формулу точного решения (12)

=D35*СТЕПЕНЬ(D33;3)/3+D36*СТЕПЕНЬ(D33;2)/2+D37*D33-(D35*СТЕПЕНЬ(D34;3)/3+D36*СТЕПЕНЬ(D34;2)/2+D37*D34) (17)

3. В ячейку F14 вводим формулу прямоугольников "с недостатком" (13)

=h * СУММ (D21:D28) (18)

4. В ячейку F14 вводим формулу прямоугольников "с избытком" (14)

=h*СУММ (D22:D29) (19)

5. В ячейку F16 вводим формулу трапеций (15)

=h/2*(D21+2*D22+2+D23+2*D24+2*D25+2*D26+2*D27+2*D28+D29) (20)

6. В ячейку F17 вводим формулу парабол (16)

=h/3*(D21+2*(D22+D24+D26+D28)+4*(D23+D25+D27)+D29) (21)

7. В соответствующие ячейки G14:G17 введем формулы определения погрешности измерений по различным формулам в процентах, например, для ячейки G14 (процент ошибки при определении площади по формуле прямоугольников "с недостатком"

=ABS(E35-E34)/E34 (22)

8. Для нахождения предпочтительного варианта вычисления воспользуемся функцией, определяющей минимальное значение в списке аргументов (ячеек G14:G17). Тогда для ячейки G20 получим

=МИН(G14:G17)

(23)

9. Полученную таблицу через буфер обмена вставляем в пояснительную записку

Таблица 4

11. Итого, в нашем случае, минимальный процент ошибки дает вычисление интеграла по формуле прямоугольников с избытком. Ошибка составляет 0,09%.

ЗАКЛЮЧЕНИЕ

Выполнив данную работу, мы научились:

1. Word.

4. Excel (работать с матрицами, строить диаграммы, пользоваться встроенными функциями и т.п.).

5. Word и Excel, входящих в пакет MicrosoftOffice.