Интеграл по комплексной переменной. Операционное исчисление и некоторые его приложения
| Загрузить архив: | |
| Файл: ref-8496.zip (175kb [zip], Скачиваний: 164) скачать |
Интеграл по комплексной переменной.
Определение 1: Кривая Г называется гладкой ,если она имеет непрерывно изменяющуюся касательную.
Определение 2: Кривая называется кусочно-гладкой ,если она состоит из конечного числа гладких дуг.
Основные свойства : Пусть на комплексной плоскостиZ задана кусочно-гладкая кривая С длинойl, используяпараметрическое задание кривой С зададим h(t) и x (t), где h и x являются кусочно-гладкими кривыми от действительнойпеременной t. Пусть a<= t<=b, причем a и b могут быть бесконечными числами .
Пусть xиh удовлетворяют условию : [x‘(t)]2 + [h‘(t)]2 ¹ 0. Очевидно, что задание координат h =h(t) и x=x (t),равносильно заданию комплексной функции z (t)= x (t) + ih(t).
Пусть в каждой точкеz (t)кривой С определена некоторая функция f (z ).Разобьем кривую С на n – частичных дуг точками деления z0 , z1 , z2 , …,z n-1соответствующие возрастающим значениям параметра t, т.е. t0, t1, …, t i+1 > t i.
Dz i =z i – zi-1. Составим
интегрируемую функцию S = åf (z*)Dz i .
(1)
гдеz*– производная точки этой
дуги.
Если при стремлении max |Dz i|®0 существует предел частных сумм не зависящий ни от способа разбиения кривой С на частичные дуги, ни от выбора точек z i , то этотпредел называется интегралом от функции f (z ) по кривой С.
 (2)
(2)
f (zi* ) = u (Pi*) + iv (Pi*) (3)
где Dz i = Dx (t) + iDh(t) (x (t) иh(t) - действительные числа)
Подставив (3) в (1) получим :

(4)
Очевидно, что (4) состоит из суммы двух частных сумм, криволинейных интегралов действительной переменной. Переходя в (4) к пределу при Dx и Dh ® 0 и предполагая, что данные пределы существуют, получаем :

(5)
Заметим, что для существования криволинейного интегралов, входящих в (5), а тем самым и для существования интеграла (2) достаточно кусочной непрерывности функций u и v. Это означает, что (2) существует и в случае неаналитичности функции f (z ).
Сформулируем некоторые свойства интеграла от функции комплексной переменной. Из равенства (5) следуют свойства :





О ограниченности интеграла.
 |
При этом z = j (z ).
7.) Пусть Cp – окружность радиуса r, с центром в точке Z0. Обход вокруг контура Cp осуществляется против часовой стрелки. Cp : z = Z0 + r×eij, 0 £j£2p, dz = ir×eij dj .
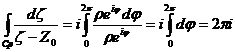
Кусочно-гладкую замкнутую кривую будем называть замкнутым контуром, а интеграл
по замкнутому контуру – контурным интегралом.
ТЕОРЕМА КОШИ.
В качестве положительного обхода контура выберем направление при котором внутренняя область, ограниченная данным замкнутым контуром остается слева от направления движения :

Для действительной переменной имеют место формулы Грина. Известно, что если
функции P(x, y) и Q(x, y) являются непрерывными
в некоторой заданной области G,
ограниченны кусочно-гладкой кривой С, а их частные производные 1-го порядка
непрерывны в G, то
имеет место формула Грина:

( 8 )
ТЕОРЕМА : Пусть в односвязной области G заданааналитическая функция f(Z), тогда интеграл от этой функции по замкнутому контуру Г целиком лежащему в G ,равен нулю.
Доказательство : из формулы (5) следует:

Т.к. f(z
) аналитическая всюду, тоU(x, y), V(x, y) - непрерывны
в области, ограниченной этим контуром и при этом выполняются условия Коши-Римана.
Используя свойство криволинейных интегралов:

Аналогично :
По условию Коши-Римана в последних равенствах скобки равны нулю, а значит и оба криволинейных интеграла равны нулю. Отсюда :

ТЕОРЕМА 2 (Вторая формулировка теоремы Коши) : Если функция f(z) является аналитической в односвязной области G, ограниченной кусочно-гладким контуром C, и непрерывна в замкнутой области G, то интеграл от такой функции по границе С области G равен нулю.
TEOPEMA 3(Расширение теоремы Коши на многосвязную область) :
 f (z)
является аналитической функцией в многосвязной области G, ограниченной извне контуром С0,
а изнутри контурами С1, С2, .. ,Сn (см. рис.). Пусть f (z) непрерывна в замкнутой
области G, тогда :
f (z)
является аналитической функцией в многосвязной области G, ограниченной извне контуром С0,
а изнутри контурами С1, С2, .. ,Сn (см. рис.). Пусть f (z) непрерывна в замкнутой
области G, тогда :

, где С – полная граница области G, состоящая из контуров С1, С2, .. , Сn. Причем обход кривой С осуществляется в положительном направлении.
Неопределенный интеграл.
 |
Следствием формулы Коши является следующее положение : пусть f(Z) аналитичнав односвязной области G, зафиксируем в этой области точку Z0 и обозначим:
интеграл по какой-либо кривой, целиком лежащей в области G, содержащей Z0 и Z, в силу теории Коши этот интеграл не зависит от выбора кривой интегрирования и является однозначной функциейФ(Z).Аналитическая функция Ф(Z) называется первообразной от функции f(Z) в области G, если в этой области имеет место равенство : Ф¢ (Z) = f( Z).
Определение: Совокупность всех первообразных называется неопределенным интегралом от комплексной функции f(Z). Так же как и в случае с функцией действительного переменного имеет место равенство :
( 9)
Это аналог формулы Ньютона-Лейбница.
Интеграл Коши. Вывод формулы Коши.


 |
Пусть функция f(Z) – аналитическая функция в односвязной области G, ограниченной контуром С. Возьмем внутри этой области произвольную точку Z0 и в области G вокруг этой точки построим замкнутый контур Г. Рассмотрим вспомогательную функцию j (Z).Эта функция аналитична в области G всюду, кроме точки Z=Z0. Проведем контурg с достаточным радиусом, ограничивающий точку Z0, тогда функция будет аналитична в некоторой двусвязной области, заключенной между контурами Г и g. Согласно теореме Коши имеем :
По свойствам интегралов :
(2 )
 g окружность gr
с радиусом r . Тогда:
g окружность gr
с радиусом r . Тогда:
(3)
Уравнение окружности gr : z = Z0 + reij (4)
Подставив (4) в (3) получим :

( 5 )

( 6 )

(7)
 gr® 0, т.е. r® 0.
gr® 0, т.е. r® 0.
Тогда т.к. функция f(z) аналитична в точке Z=Z0 и всюду в области G, а следовательно и непрерывна в G, то для всех e>0 существует r>0, что для всех z из r–окрестности точки Z0 выполняется | f(z) – f(Z0) | < e.


(8)
Подставив ( 7) в ( 6) с учетом ( 8) получаем :

Подставляя в ( 5)и выражая f(Z0) имеем :
(9)
 интеграл Коши.
интеграл Коши.
Интеграл, стоящий в (9) в правой части выражает значение аналитической функции f(z) в некоторой точке Z0 через ее значение на произвольном контуре g , лежащем в области аналитичности функции f(z) и содержащем точку Z0 внутри.
Очевидно, что если бы функция f(z) была аналитична и в точках контура С, то в качестве границы g в формуле (9) можно было использовать контур С.
Приведенные рассуждения остаются справедливыми и в случае многосвязной области G.
Следствие : Интеграл Коши, целиком принадлежащий аналитической области G имеет смысл для любого положения Z0 на комплексной плоскости при условии, что эта точка есть внутренней точкой области Г. При этом если Z0 принадлежит области с границей Г, то значение интеграла равно (9), а если т.Z0 принадлежит внешней области, то интеграл равен нулю :

При Z0 ÎГ
указанный интеграл не существует.
Интегралы, зависящие от параметра.
Рассматривая интеграл Коши, видим, что подинтегральная функция зависит от 2-х комплексных переменных : переменной интегрирования z и Z0. Таким образом интеграл Коши может быть рассмотрен как интеграл, зависящий от параметра, в качестве которого выбираем точку Z0.
Пусть задана функция двух комплексных переменных j (Z, z ), причем Z= x + iyв точке, принадлежащей некоторой комплексной плоскости G. z= x+ ih ÎС.(С - граница G).
Взаимное расположение области и кривой произвольно. Пусть функция j (Z, z )удовлетворяет условиям : 1) Функция для всех значений z Î С является аналитической в области G. 2) Функция j (Z, z )и ее производная ¶j/¶Z являются непрерывными функциями по совокупности переменных Z и z при произвольном изменении области G и переменных на кривой С. Очевидно, что при сделанных предположениях :

Интеграл существует и является функцией комплексной переменной. Справедлива
формула :
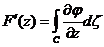 (2)
(2)
Эта формула устанавливает возможность вычисления производной от исходного интеграла путем дифференцирования подинтегральной функции по параметру.
ТЕОРЕМА. Пусть f(Z) является аналитической функцией в области G и непрерывной в области G (G включая граничные точки ), тогда во внутренних точках области G существует производная любого порядка от функции f(Z) причем для ее вычисления имеет место формула :

(3)
С помощью формулы (3) можно получить производную любого порядка от аналитической функции f (Z) в любой точке Z области ее аналитичности. Для доказательства этой теоремы используется формула (2) и соответственные рассуждения, которые привели к ее выводу.
ТЕОРЕМА МОРЕРА. Пусть f(Z) непрерывна в односвязной области G и интеграл от этой функции по любому замкнутому контуру, целиком принадлежащему G равен 0. Тогда функция f (Z) является аналитической функцией в области G. Эта теорема обобщается и на случай многосвязной области G.
Разложение функции комплексного переменного в ряды.
Если функция f(x, y) определена и непрерывна вместе с частными производными (до n-го порядка ), то существует разложение этой функции в ряд Тейлора :
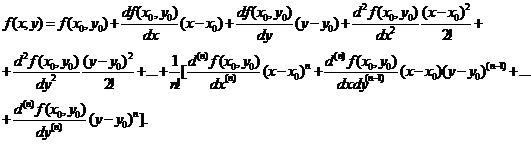
Итак, если задана функция f (z) комплексного переменного, причем f (z) непрерывная вместе с производными до n-го порядка, то:
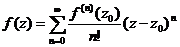 (2) – разложение в ряд Тейлора.
(2) – разложение в ряд Тейлора.
Формула (2) записана для всех Z принадлежащих некоторому кругу | Z-Z0
| Функция f
(z), которая может быть представлена в виде ряда (2) является
аналитической функцией. Неаналитическая функция в ряд Тейлора не
раскладывается. Причем | Z
| < R,R ® ¥ . Формулы ЭЙЛЕРА. Применим разложение (3) положив, что Z = ixи Z=
- ix; Аналогично взяв Z = - ix получим : Из (6) и (7) можно выразить т.н. формулы Эйлера : В общем случае : Известно, что : Тогда из (9) и (10) вытекает связь между тригонометрическими
и гиперболическими косинусами и синусами: Ряд ЛОРАНА. Пусть функция f(z) является аналитической функцией в
некотором круге радиусом R, тогда ее можно разложить в ряд Тейлора (2). Получим
тот же ряд другим путем. ТЕОРЕМА 1. Однозначная функция
f(Z) аналитическая в круге радиусом
|Z-Z0| < R раскладывается в сходящийся к ней степенной ряд
по степеням Z-Z0. Опишем в круге радиусом R окружность r, принадлежащую кругу
с радиусом R. Возьмем в круге радиуса r точку Z, а на
границе области точку z , тогдаf(z) будет аналитична внутри круга с радиусом
r и на его границе.
Выполняется условие для существования интеграла Коши : Поскольку Представим равномерно сходящимся рядом в круге радиуса r, умножая (12) на 1/(2pi) и интегрируя по L при фиксированном Z, получим
: слева интеграл (13) который равен f (Z), а справа будет сумма интегралов : Обозначая Это разложение функции f (Z) в круге R в ряд Тейлора. Сравнивая (14) с рядом (2)
находим, что ТЕОРЕМА 2. Если однозначная функция f(Z) аналитична вне круга с радиусом r с центром в точке Z0
для всех Z выполняется неравенство r < |Z-Z0 |, то она
представляется рядом : гдеh - ориентированная против часовой
стрелкиокружность радиуса r (сколь угодно большое
число). Если обозначить ТЕОРЕМА 3. Если однозначная функция f(Z) аналитическая в кольце Z< |Z-Z0 | f1
и f2 можно представить в виде
двух рядов : Ряд (19) – ряд Лорана, при этом ряд (20) сходится в круге
радиуса R, ряд (21)
сходится вне круга радиуса R функции
f2(Z). Общая область сходимости ряда – кольцо между r и R. f1(Z)
– правильная часть. f2(Z) – главная часть ряда Лорана. Ряд Тейлора – частный случай ряда Лорана при отсутствии
главной его части. Классификация изолированных особых точек. Вычеты. Определение 1. Особой точкой функции f(Z) определенной в
области (замкнутой) G, ограниченной Жордановой кривой, называется точка Z=Z0 Î
G в которой аналитичность функцииf1(Z)
нарушается. Рабочая точка Z=Z0 функции f(Z), ограниченной в круге |Z-Z0| 1) 2) 3) Если С-n=0, то особая точка есть устранимая
особая точка. Пусть f(Z0)=C0 и C-nдля всехn=1,2,3,..,m отличного от 0, а для всехn ® m+1 C-n=0, тогда Z=Z0 будет
являться полюсом порядкаm. При m>1 такой полюс будет называться простым. Определение 2. Вычетом функции f(Z) в круге|Z-Z0| Если полюс имеет кратность m ³1,
то для определения вычетов используется формула : при m=1 : Основная теорема о
вычетах. Пусть f(z) аналитическая
в области G кроме
конечного числа полюсов Z = a1, a2, …, ak. g–произвольный,
кусочно-гладкий замкнутый контур содержащий внутри себя эти точки и целиком
лежащий внутри области G.
В этом случае интеграл Пример : Найти вычет Особые точки : Z1=1, Z2= - 3. Определим порядок полюсов – все полюсы первого порядка. Используем формулу (3) :  (3)
(3) (4)
(4) (5)
(5)

 (6)
(6) (7)
(7) (8)
(8) (9)
(9) (10)
(10)
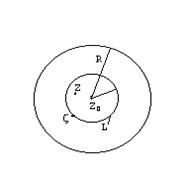
 (13)
(13) (11)
(11)
 можно представить как
сумму бесконечно убывающей геометрической прогрессии со знаменателем
можно представить как
сумму бесконечно убывающей геометрической прогрессии со знаменателем 


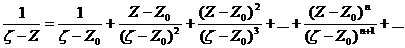 (12)
(12)

 (14)
(14)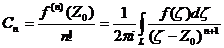 (15)
(15) (16)
(16) (17) , получим :
(17) , получим :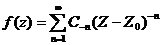 (18)
(18) (19)
(19) (20)
(20) (21)
(21)

 не существует, то
точка Z=Z0называется
существенной особой точкой.
не существует, то
точка Z=Z0называется
существенной особой точкой.
 ® ¥ , то в этом
случае в точке Z=Z0
имеем существенную особенность.
® ¥ , то в этом
случае в точке Z=Z0
имеем существенную особенность.
 (3)
(3)
 a1, a2, …, akи т.д. умноженный на 2pi :
a1, a2, …, akи т.д. умноженный на 2pi : (5)
(5)

